时标上2阶动态方程非线性边值问题
2012-09-09钟文勇
钟文勇
(吉首大学数学与统计学院,湖南吉首 416000)
时标上2阶动态方程非线性边值问题
钟文勇
(吉首大学数学与统计学院,湖南吉首 416000)
研究了时标上一类2阶动态方程的非线性边值问题,利用2个算子和的不动点定理,得到非线性边值问题至少存在1个解的充分条件.
时标;动态方程;非线性边值问题;不动点
时标及时标上的微积分理论主要目的在于“统一与推广”,即统一和推广现有的微积和差分以及常微分方程和差分方程的理论[1].目前,这一理论正得到迅速发展.因为,一方面,它统一和推广了经典的微分和差分理论,另一方面,时标上动态方程的研究也在真实现象和过程的数学模型中具有重要应用[2],例如时标上的种群动力学、流行病模型、金融消费过程的数学模型等[3-4].总之,时标和时标上的动态方程理论有广阔的应用前景.近年来,时标上动态方程的边值问题的研究一直是该类系统研究的重要问题之一,并得到一些结果,但是,关于时标上动态方程的非线性边值问题的结果很少[5],有待进一步研究.
笔者主要研究如下时标上2阶非线性边值问题:

其中:f(t,x)是定义在T T×R上的实值函数,T T为时标,R表示全体实数集;g1,g2为定义在给定的函数空泛函.
1 预备知识
一个时标T T是实数集R的一个任意闭子集,它具有由R诱导的拓扑即顺序关系.本节的主要内容参考文献[2].
定义1 设t∈T T,定义前跃算子σ:T T|→T T和后跃算子ρ:T T|→T T分别为

规定infØ=sup T T,supØ=inf T T.
设t∈T T,若σ(t)=t,则t称为右稠密点;若σ(t)>t,则t称为右扩散点;若ρ(t)=t,则t称为左稠密点;若ρ(t)>t,则t称为左扩散点.为了度量时标上相邻点的位置关系,定义尺度函数μ:T T|→R为μ(t)=σ(t)-t.
设a,b∈T T,定义T T中的闭区间为[a,b]TT={t∈T T:a≤t≤b}.T T中的其他类型的区间可类似定义.
现介绍时标上的Δ-导数、Δ微积分的定义.由T T可定义集合T Tk:若sup T T<∞,则T Tk=T T\(ρ(sup T T),sup T T];若sup T T=∞,则T Tk=T T.
定义3 假设f:T T|→R,对于给定的t∈T Tk,若存在γ(t)∈R,对任意给定的∈>0,存在t的邻域UTT使得对任意s∈UTT,不等式

成立,则称γ(t)为函数f在t点的Δ-导数,并记fΔ(t)=γ(t).
记σ0(b)=b,σ1(b)=σ(b),σ2(b)=σ(σ(b)),Ii=[a,σi(b)]TT(i=0,1,2).C(I)表示定义在区间I上全体实值连续函数构成的空间,‖·‖I表示C(I)的上确界范数,即.再记

则CΔ(I2)在范数‖x‖=max{‖xΔ‖I1,‖x‖I2}下成为Banach空间.
设g1:C(I1)|→T T,g2:CΔ(I2)|→R是给定的泛函.
定义4 若x∈CΔ(I2),xΔΔ(t)∈Crd(I0),并且(1)式成立,则称x(t)为边值问题(1)的解.
引理1[6]设B是Banach空间,U是B的凸闭子集V中的开集,假设0∈U,T(¯U)有界,T=T1+T2:¯U|→V,其中T1:¯U|→B是全连续算子,T2:¯U|→B是非线性压缩算子(即存在连续单调非减函数φ:[0,∞)|→[0,∞),φ(z)<z(z>0),使得对任意x,y∈¯U,均有‖T2(x)-T2(y)‖≤φ(‖x-y‖)),则必然有:(ⅰ)T在¯U中有一不动点;(ⅱ)或存在u∈∂U满足u=λT(u),λ∈(0,1).这里,¯U和∂U分别表示U的闭包和边界.
2 主要结果
首先,研究边值问题(1)对应的线性问题解的存在性,为此,引入假设:
(H1)g1:C(I1)|→R,g2:CΔ(I2)|→R,且gi(0)=0.存在非负常数l1,l2满足l1≤1,l2≤1,l1· max{1,(σ2(b)-a)}+l2=l<1,并使得对任意x,y∈C(I1)∩CΔ(I2),均有|gi(x)-gi(y)|≤li‖x-y‖Ii(i=1,2)成立.
引理2 假设h:T T|→R是连续的,若条件(H1)成立,则边值问题

存在唯一解,且解可表示为

由(2)式中的边界条件可确定x(a),xΔ(a),得到
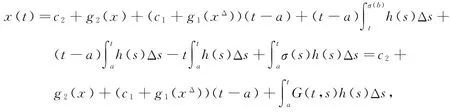
其中G(t,s)由(3)式确定.
再证明唯一性.若x=x(t),y=y(t)均为(2)式的解,则
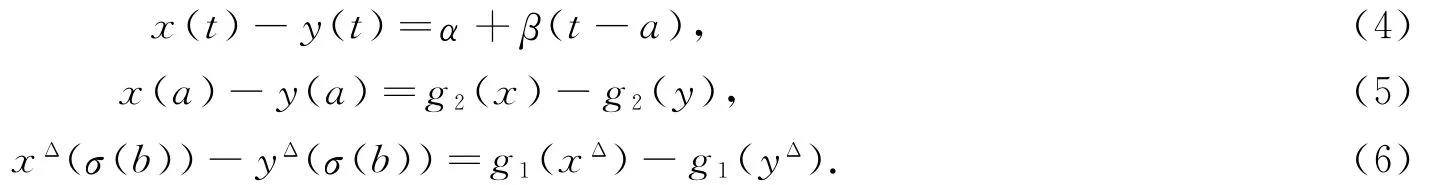
由(4)至(6)式及假设(H1)可知,
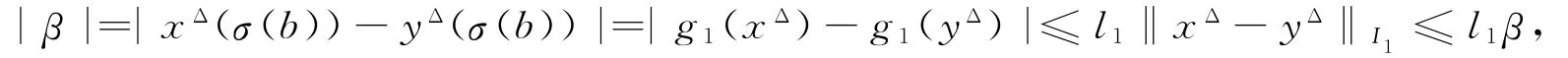
因此β=0.进一步有估计

这导出α=0.从而x(t)=y(t),t∈I2.证毕.
现作假设:
(H2)f:I2×R|→R连续.
类似于引理2的证明,可得到如下结果:
引理3 若假设(H1),(H2)成立,则边值问题(1)等价于积分方程

由引理2,3可知算子T的定义是明确的,且边值问题(1)等价于算子T的不动点问题.不难验证T:CΔ(I2)|→CΔ(I2).再定义算子
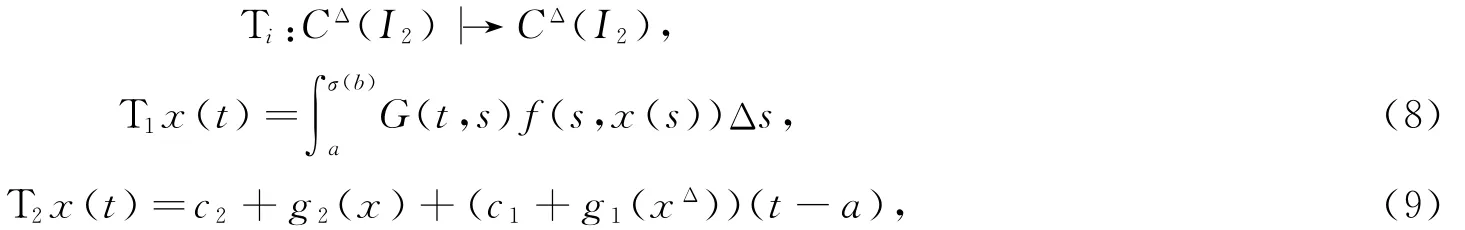
则T=T1+T2.
为应用引理1研究边值问题(1),现给出T1,T2的几个重要性质.
设r是正实数,Ωr={x∈CΔ(I2):‖x‖<r}.
引理4 若条件(H1),(H2)满足,则是全连续算子.
证明 首先证明T1连续.

由估计(10)及假设(H1)可得

综合上述证明可知T1是全连续的.
为陈述和证明主要定理,进一步引入以下基本假设:
(H3)存在非负函数p∈L1(I2)和单调非减函数ψ:[0,∞)|→[0,∞),并且p在I2的具有正Δ-测度的子集上大于0,使得对任意(t,u)∈I2×R,成立|f(t,u)|≤p(t)ψ(|u|).这里,L1(I2)表示在I2上LebesgueΔ-可积实函数的集合.

定理1 若(H1)至(H4)成立,则边值问题(1)至少存在1个解.
证明 设算子T,T1,T2分别由(7)至(9)式定义.由引理2,3可知算子T的不动点就是边值问题(1)的解.
以下证明算子T,T1,T2满足引理2相应条件,从而存在不动点.
由(H4)知,存在r>0使得

最后,证明引理1的结论(ⅱ)不成立.假若(ⅱ)成立,则存在λ∈(0,1),x∈∂Ω使得x=λT x,于是
可得到

综上所述,由引理1知算子F在¯Ωr至少有1个不动点,即边值问题(1)至少存在1个解.证毕.
[1] HILGER S.Analysis on Measure Chain-A Unified Approach to Continuous and Discrete Calculus[J].Journal of Results Math.,1990,18:18-56.
[2] BOHNER M,PETERSON A.Dynamic Equations on Time Scales[M].Boston:Birkhauser,2001.
[3] SHENG Q,FADAG M.An Exploration of Combined Dynamic Derivatives on Time Scales and Their Applications[J].Nonlinear Analysis:Real World Applications,2006,7(3):395-413.
[4] ATICI F M,BILES D C,LEBEDINSKY A.An Application of Time Scales to Economics[J].Math.Compu.Modelling,2006,43(7-8):718-726.
[5] 钟文勇.时标上二阶脉冲动态方程的非局部边值问题[J].复旦学报:自然科学版,2009(2):245-252.
[6] O’REGAN D.Fixed-Point Theory for the Sum of Two Operators[J].Appl.Math.Lett.,1995,9(1):1-8.
Nonlinear Boundary Value Problem for Second Order Dynamic Equations on Time Scales
ZHONG Wen-yong
(School of Mathematics and Statistics,Jishou University,Jishou 416000,Hunan China)
This paper deals with the nonlinear boundary value problem for the second order dynamic equations on time scales.Using fixed-point theorem for the sum of two operators,some sufficient conditions are obtained to guarantee the existence of at least one solution of the boundary value problem.
time scales;dynamic equation;nonlinear boundary value problem;fixed point
book=83,ebook=166
O175.8
A
10.3969/j.issn.1007-2985.2012.04.002
(责任编辑 向阳洁)
1007-2985(2012)04-0006-05
2012-04-25
湖南教育厅科学研究项目(10C1125)
钟文勇(1963-),男,湖南吉首人,吉首大学数学与统计学院副教授,博士,主要从事微分方程研究.
