可溶性气体泡沫状态方程理论模型研究

李遵照，吴信荣，李兆敏，肖 良

(1.中石化中原油田分公司，河南 濮阳 457001;2.中国石油大学，山东 东营 266555)

可溶性气体泡沫状态方程理论模型研究

李遵照1，吴信荣1，李兆敏2，肖 良1

(1.中石化中原油田分公司，河南 濮阳 457001;2.中国石油大学，山东 东营 266555)

考虑气体在地层水中的溶解度、矿化度和表面张力引起的气泡内外压差等因素对气体泡沫体积性质的影响，推导出气体泡沫的理论状态方程，并结合分析对该模型进行了化简，对泡沫的气相和液相分别选择了合适的密度模型。计算结果表明，泡沫理论状态方程具有较好的计算精度和满意的预测能力，能够用于理论分析和现场应用。

可溶性气体;泡沫状态方程;密度计算;CO2泡沫

引 言

泡沫流体在石油工业的钻井［1］、油气井增产、修井和提高采收率［2］等方面都显示出很大的应用潜力，逐渐形成了泡沫流体增产系列技术［3］。泡沫体系的密度对施工设计是一个不可或缺的参数，发展泡沫体系的理论状态方程估算该体系的密度，用以指导设计以及进行其他理论研究是十分必要的。目前一般假设泡沫中液相不可压缩、气相为实际气体来计算泡沫密度。但是气相分散到液相形成泡沫后，其可压缩性与气液两相单独存在的可压缩性并不相同［3］。

Ejofodomi E A等［4］基于3点假设推导出了N2(非溶解性气体)气体泡沫理论状态方程。王冠华等［5］在此基础上，考虑气相在液相中的溶解并忽略因溶解气体导致液相的体积变化，推导出CO2泡沫的理论状态方程。以上建立的方程都能在一定程度上描述泡沫的PVT性质，但是所作的假设与实际泡沫体系的性质还有差距:①高压下，压力对于液相的压缩性需要考虑;②溶解性气体的溶入对起泡剂溶液的体积性质影响;③实际的起泡剂溶液往往具有较高的矿化度，甚至一些起泡剂溶液中含有高分子物质作为稳泡剂或者调剖剂，起泡剂溶液中含有的这些无机盐和有机物对液相的体积性质具有重要的影响;④液相中起泡剂的存在是起泡体系能够发泡的关键，起泡剂对起泡体系的影响需要在泡沫状态方程中进行考虑。基于以上4点，本文建立了溶解性气体的泡沫状态方程，以CO2泡沫为例，建立了CO2泡沫的密度模型。

1 气体泡沫理论状态方程的推导

为了推导溶解性气体泡沫状态方程，做以下几点假设:①考虑气相在液相中的溶解;②忽略起泡剂中的表面活性剂分子之间及其与气相和液相中气体分子的相互作用;③考虑起泡剂溶液中无机盐对气体溶解度和液相密度的影响;④考虑表面张力引起的气泡大小因素对气泡内外压力差和气相密度的影响。

泡沫体系的密度方程为:

式中:ρf为泡沫密度，kg/m3;mf为泡沫质量，kg;Vf为泡沫体积，m3。

泡沫体系的质量方程为:

式中:mg为产生泡沫前气体质量，kg;ml为起泡剂溶液质量，kg。

液相中溶解的气体质量为:

式中:x为气体在液相中的溶解度，mol/kg;Δmg为液相中溶解的气体质量，kg;M为气体的摩尔质量，kg/mol。

式中:Δp为单个气泡的内外压力差，MPa;r为泡沫体系泡沫的平均半径，m;γ为起泡体系的表(界)面张力，mN/m。

气泡内部压力为:

式中:p'为气泡内部压力，MPa;p为气体泡沫体系的压力，MPa。

式(10)中，由于气泡内外的压差与体系压力相比非常小，因此可以忽略，即p'=p。

气体状态方程为:

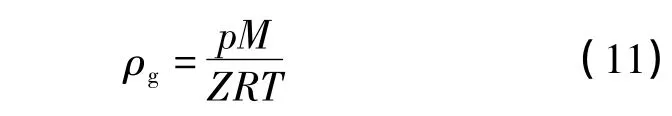
式中:T为温度，K;Z为气体压缩因子;R为气体常数。

将式(11)代入式(8)可得:

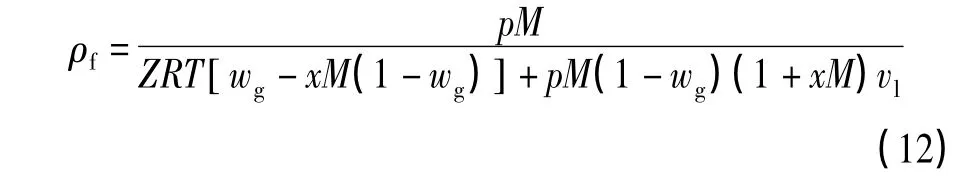
式中:vl为液相的比容，m3/kg。

式(12)是气体泡沫状态方程，下面以可溶性气体CO2形成的泡沫为例，应用此模型进行气体泡沫密度计算。

2 气(液)相CO2密度计算

计算CO2密度首先要计算CO2在一定温压条件下的压缩因子［6］。本文采用Duan等建立的针对超临界CO2的状态方程［7］，其表达式为:

式中:Tr、pr、Vr分别为对比温度、对比压力和对比体积;a1、a2……a15为参数，计算方法参见文献［7］。

3 CO2在地层水中的溶解度

CO2在地层水中的溶解度需要考虑地层水中所含盐离子对CO2溶解度的影响。本文CO2在地层水中的溶解度计算式采用Duan和Sun提出的计算模型［7－8］，其表达式如下。

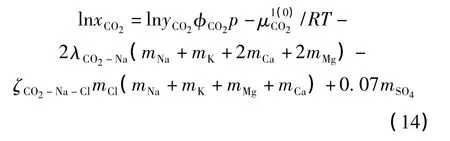
由于在273～533 K温度范围内，CO2－H2O混合物体系的气相中CO2的逸度系数与纯CO2的逸度系数差别很小［7］。因此，φCO2可以用纯CO2的逸度系数代替。本文采用Duan等建立的CO2逸度系数模型［8］，该模型表达式如下。

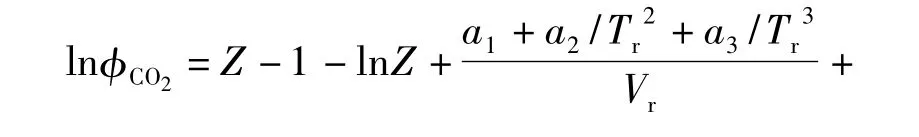
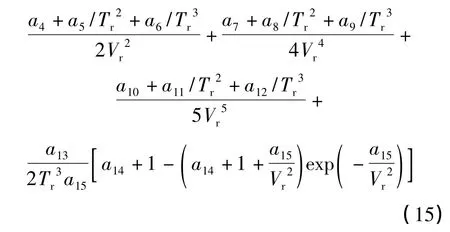
由于现在还没有CO2－H2O－NaCl－MgCl2－CaCl2体系气相组成数据发表，因此，式(14)中yCO2可以通过下式计算:

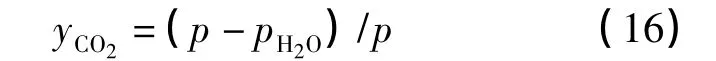
式中:pH2O为纯水的饱和蒸汽压力，bar。

pH2O采用实验拟合公式计算:

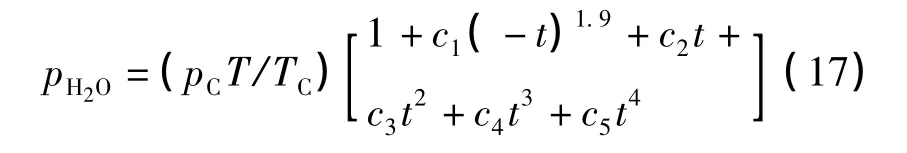
式中:t=(T－Tc)/Tc;Tc为水的临界温度，K;pc为水的临界压力，bar;参数 c1、c2、c3、c4、c5数值见文献［7］。

4 CO2－H2O－NaCl体系密度

VH2O可以采用IAPWS97 EOS精确计算［10］。为方便计算，本文采用 Hu等［11］建立的纯水摩尔体积计算模型，见公式(20)。此模型计算值与Wagner和 Pruss的实验值［12］(温度范围为 273.15～473.15 K，压力范围为0～200 MPa)平均偏差为0.005%，最大偏差为0.027%。

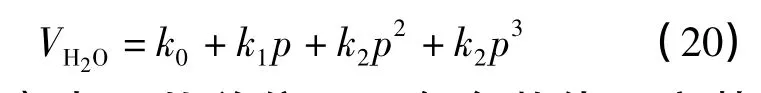
式(20)中 p的单位 bar，各参数值见文献［11］。

5 计算与分析

采用本文建立的CO2泡沫状态方程计算CO2泡沫密度，并与王冠华等［5］测量的不同条件下的实验值进行了对比。图1～3是气体质量分数为0.413 5，温度分别为 40、60、80℃，压力在 5 ～30 MPa下的CO2泡沫密度。从图中实验值和计算值对比可以看出，本文建立的气体泡沫状态方程对CO2泡沫密度计算结果与实验值吻合较好，平均相对偏差为4.5%。压力高于临界压力时，相对偏差增大。整体而言，本模型能够用于CO2泡沫体积性质的计算。

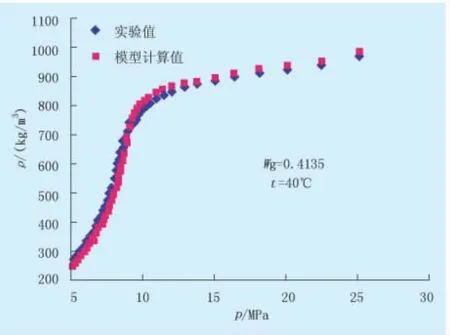
图1 CO2泡沫密度随压力变化

图2 CO2泡沫密度随压力变化

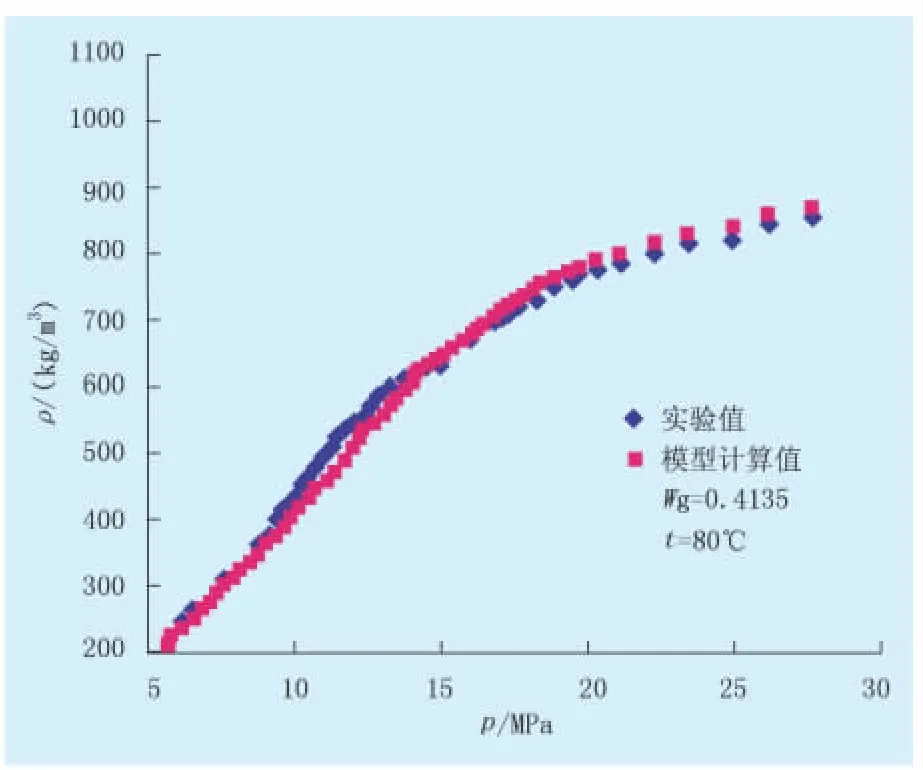
图3 CO2泡沫密度随压力变化

图4显示了矿化度(NaCl)对CO2泡沫密度的影响。从图中可以看出随着地层水矿化度的增大，CO2在液相中的溶解度减小，液相密度增大，泡沫密度增大。

图4 CO2泡沫密度随压力变化

6 结论

(1)考虑气体在地层水中的溶解度、矿化度和表面张力引起的气泡内外压差等因素对气体泡沫体积性质的影响，推导出可溶性气体泡沫的理论状态方程，并结合分析对该模型进行了化简。

(2)CO2泡沫密度计算结果表明，该模型计算值与实验值吻合较好，平均相对偏差为4.50%，能够满足工程计算需要。

(3)CO2泡沫密度随着地层水矿化度的增大而增大，因此，计算泡沫密度时必须考虑矿化度对气体溶解度和液相密度的影响。

［1］马勇，崔茂荣，孙少亮，等.可循环微泡沫钻井液体系［J］.特种油气藏，2005，12(2):5－8.

［2］殷方好，刘慧卿，杨晓莉，等.千12块稠油油藏转氮气泡沫驱研究［J］.特种油气藏，2010，17(3):80－82.

［3］李兆敏.泡沫流体在油气开采中的应用［M］.北京:石油工业出版社，2009:1－2.

［4］Ejofodomi E A，Zhu D.Evaluating bottom hole pressure for foamed acid stimulation［C］.SPE98163，2006:1 －6.

［5］王冠华，李兆敏，李宾飞，等.CO2泡沫状态方程的理论模型研究［J］.石油化工高等学校学报，2010，23(4):68－72.

［6］薛卫东，朱正和，邹乐西，等.超临界CO2热力学性质的理论计算［J］.原子与分子物理学报，2004，21(2):295－300.

［7］Duan Z，Sun R.An improved model calculating CO2solubility in pure water and aqueous NaCl solutions from 273 to 533K and from 0 to 2000bar［J］.Chemical Geology，2003，193(3－4):257－271.

［8］Duan Z，Sun R，Zhu C，et al.An improved model for the calculation of CO2solubility in aqueous solutions containing Na+，K+，Ca2+，Mg2+，Cl－and SO42－［J］.Marine Chemistry，2006，98(2 －4):131 －139.

［9］Duan Z，Hu J，Li D，et al.Densities of the CO2– H2O and CO2–H2O–NaCl Systems Up to 647K and 100MPa［J］.Energy ＆ Fuels，2008，22(3):1666 －1674.

［10］李春曦.工业用水和水蒸气热力性质计算公式— —IAPWS －IF97［J］. 锅炉技术，2002，33(6):15－19.

［11］Hu J，Dun Z，Zhu C，et al.PVTx properties of the CO2–H2O and CO2–H2O–NaCl systems below 647K:Assessment of experimental data and thermodynamic models［J］.Chemical Geology，2007，238(3 － 4):249 －267.

［12］Wagner W，Pruss A.The IAPWS formulation 1995 for the thermodynamic properties of ordinary water substance for general and scientific use［J］.J Phys Chem Ref Data，2002，31(2):387 －535.

［13］Rogers，P S Z，Pitzer K S.Volumetric properties of aqueous sodium chloride solutions［J］.J Phys Chem Ref Data，1982，11(1):15 －81.

Study on the theoretical model of soluble gas foam state equations

LI Zun － zhao1，WU Xin － rong1，LI Zhao － min2，XIAO Liang1
(1．Zhongyuan Oilfield Company，SINOPEC，Puyang，Henan457001，China;
2．China University of Petroleum，Dongying，Shandong266555，China)

A theoretical model of state equations of gas foam is derived and simplified by considering the impacts of gas solubility，formation water salinity and surface tension on foam volume．Suitable density models are selected respectively for gas phase and liquid phase．Calculation results indicate that the theoretical state equations of gas foam can be applied to theoretical analysis and field practice with high calculation accuracy and satisfactory prediction capability．

soluble gas;state equation of foam;density calculation;CO2foam

TE357.46

A

1006－6535(2012)01－0078－04

20110603;改回日期20110930

国家油气科技重大专项“砂岩油藏长期开采后窜流规律及治理方法”(2008ZX05009－004－02)

李遵照(1981－)，男，工程师，2004年毕业于中国石油大学(北京)化学工程与工艺专业，2010年毕业于中国石油大学(北京)化学工程技术专业，获博士学位，现从事提高原油采收率工作。

编辑 孟凡勤