临界功率理论在龙舟运动训练中的应用
2012-01-02方志军李兵
方志军,李兵
(1.东北师范大学 体育学院,吉林 长春 130024;2.东北电力大学 体育学院,吉林 长春 132012)
临界功率理论在龙舟运动训练中的应用
方志军1,李兵223
(1.东北师范大学 体育学院,吉林 长春 130024;2.东北电力大学 体育学院,吉林 长春 132012)
运用临界功率理论,结合龙舟项目运动员不同距离的供能特点,探索应用龙舟测功仪训练运动员体能的手段,确立了龙舟运动员P-t、D-t、D-P、P-D-1数学模型,找到不同距离临界功率训练的区间。研究表明:1)P-t模型成非线性,曲线底端接近临界功率点。2)D-t模型成线性,直线的斜率代表了临界功率值。3)D-P模型成非线性,临界功率(CP)值是这个双曲线函数的一支渐近线与功率(横轴)的交点。4)P-D-1模型成线性,截距代表了运动员的有氧工作能力,函数的斜率代表了运动员的无氧工作能力。
运动训练;龙舟运动;临界功率
龙舟运动正在从传统的群众性娱乐项目逐步向竞技化转变,如何快速地提高龙舟运动员的训练水平,提升竞技能力是龙舟竞技发展的主要方向[1]。多年来,为获取人体供能系统的信息,已建立起的方法很多,虽然不同的有氧或无氧测试间有相关性,但各存在一些方法学的问题,还都不能满足龙舟运动的选材、训练和监测的需要,无论在理论上还是实践中,体能测试方法不仅越来越要求具备高的有效性、可靠性和全面性(采用一次性测试同时评价有氧、无氧代谢能力),而且要具备简便、无损伤易于专项化等特点[2]。临界功率(CP)理论由Scherrert和Monod[3]1960年提出,研究极限强度运动的下限,现已在径赛、自行车、游泳、赛艇等项目上应用,为体能评定开辟了新的途径,符合了目前体能评定的要求[4-5]。本文旨在探求临界功率理论在龙舟运动训练中的应用,从而初步确立龙舟运动临界功率的模型。
1 研究对象与方法
1.1 研究对象
研究对象为首届世界大学生龙舟锦标赛冠军东北电力大学队男子桨手9名,年龄(20.15±0.30)岁、身高(1.78±0.03) m、体重(72.42±1.96) kg,无伤病,测试前14 h内无剧烈运动。
1.2 研究方法
测试在中国龙舟训练科研基地训练馆内进行,室温 22 ℃。应用祥瑞龙舟测功仪分别测试每名龙舟运动员全力划250、500、1 000和2 000 m的运动时间、平均功率;用polar团队心率仪测试运动后即刻心率。运动后取指血10 μL,用便携式血乳酸测试仪测定每名运动员的血乳酸浓度。测试时间为每天上午09:00,连续测试4 d。应用SPSS17.0对所测得的数据进行统计处理。
2 结果与分析
2.1 不同距离运动测试成绩、运动后即刻心率、平均功率和血乳酸的变化
9名运动员全力划龙舟250、500、1 000、2 000 m后的平均时间、平均功率、运动后即刻平均心率、血乳酸值见表1。
表1 不同距离运动时间、平均功率、运动后即刻心率和血乳酸(±s)变化
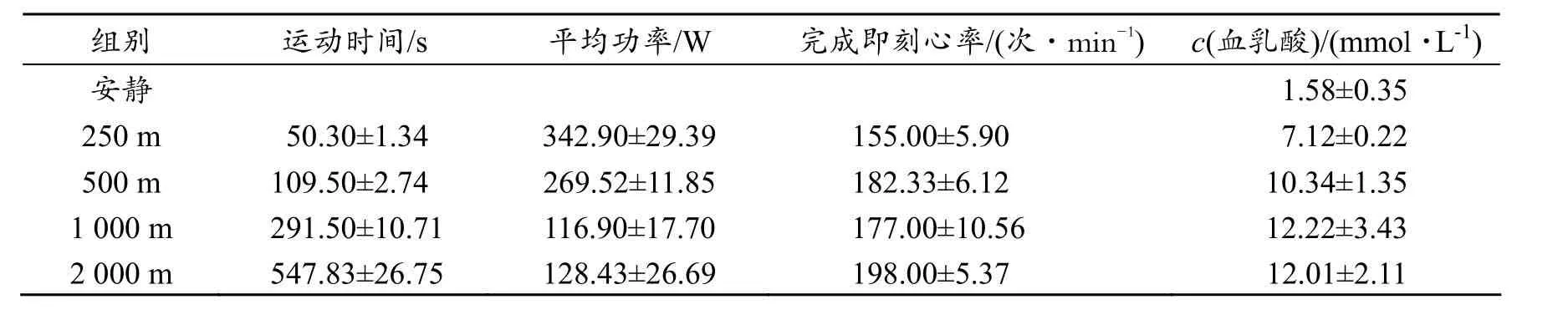
表1 不同距离运动时间、平均功率、运动后即刻心率和血乳酸(±s)变化
组别 运动时间/s 平均功率/W 完成即刻心率/(次·min-1) c(血乳酸)/(mmol·L-1)安静 1.58±0.35 250 m 50.30±1.34 342.90±29.39 155.00±5.90 7.12±0.22 500 m 109.50±2.74 269.52±11.85 182.33±6.12 10.34±1.35 1 000 m 291.50±10.71 116.90±17.70 177.00±10.56 12.22±3.43 2 000 m 547.83±26.75 128.43±26.69 198.00±5.37 12.01±2.11
2.2 龙舟运动员临界功率关系模型的建立
通过对9名龙舟运动员在龙舟测功仪上进行全力划250、500、1 000和2 000 m距离测试,记录测试结果,将结果输入 SPSS软件,利用拟合曲线得出划桨功率与时间的变化曲线,建立了P-t模型(见图1)。该模型的数学拟合线的趋势与 Hopkins等[6]的最大瞬间功率模式W=AWC+(CP×t)的P-t关系曲线十分接近。在P-t模型的下段可以看出龙舟运动员在全力负荷运动下CP接近100 W而最大输出功率在300 W左右。在运动过程中运动员输出功率为(177.35±61.21) W。从模型可以看出,运用临界功率理论,随着时间的延长,功率在逐渐的缩小,可见临界功率只有维持在一段时间内,才能使运动员达到最佳的运动状态。(AWC:无氧能力,CP:临界功率(代表有氧能力),t:时间,P:功率,W:功)
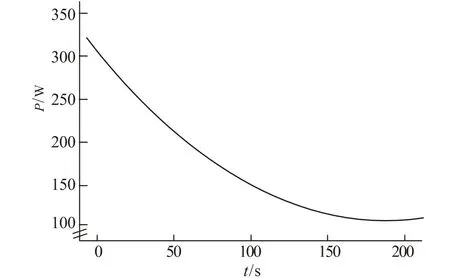
图1 P-t模型
由于距离与时间、功都成正相关,所以本研究根据龙舟运动训练的特点和实际需要,在总结前人研究成果的基础上,对应地在数学关系上进行了互换,在实际应用临界功率理论时,把测得的数据根据不同的关系按需要分成2类关系模型:1)D-t模型(见图2):D=AWC+CP×t。2)D-P模型(见图 3):D=AWC/(P-CP)。(D:距离)

图2 D-t模型
D-t模型,是在临界功率-时间W=AWC+(CP×t)[7]关系模型基础上建立的,由于距离与功正相关,本研究通过数学的方法对原有参数进行转化,结合实验数据统计结果得出:临界功率(CP)值在这个模型中是直线的斜率(4.18)反映了有氧能力的大小,AWC是直线与距离(D)轴的截距值(168.48 m),可理解为运动开始阶段的无氧代谢能力的贮备值。通过模型可以看出,直线的斜率(CP)越大,AWC的储备值越大,完成比赛的用时就越短,成绩越好。
D-P模型是在时间-功率t=AWC/(P-CP)[8]关系模型基础上建立的,由于距离与功成正相关,临界功率(CP)值是这个双曲线函数的一支渐近线与功率(横轴)的交点,为 179.13W,无氧能力(AWC)则是双曲线的曲率值(8.2×104),这个结果与Hagerman[9]和Jones等[10]建立的非线性模型基本吻合。通过模型可以看出,按照CP进行训练,无氧能力(AWC)值越大,曲线的曲率越大,所输出的功率也就越大,运动员在比赛冲刺阶段表现出的做功能力也就越强。
2.3 结合龙舟运动训练的评价方法
通过实验表明,虽然 CP的供能方式与持续时间存在双曲线关系,但临界功率毕竟是一种高于乳酸阈值的运动强度,其无氧供能已占有一定的比例,同时又低于最大耗氧量的运动强度,与无氧阈、通气阈等生理指标有着显著的相关关系。因此,它应该处于一种无氧与有氧共同供能的运动状态,只是在供能的比例上有所不同而已。
为了使图3非线性模型使用起来更方便,可通过数学上的变化,将距离参数取倒数后,把反比例双曲线函数变成正比例直线函数,在进行一元线性回归分析后建立了P-D-1模型(见图 4),临界功率中(CP)值在这个模型中是直线与功率轴的截距值,AWC是斜率,CP值在理论上被看作是最大有氧能力训练练习的有效强度。通过这种模型,除评定体能外还能控制训练的强度。为了符合龙舟测功仪训练和控制强度的习惯,换算成测功仪电子显示屏上的强度显示距离,这也正是临界功率中理论在不同专项中应用的灵活之处。例如:用“P-D-1模型”对龙舟运动员进行在临界功率强度下训练的机能评定方法,同一个测试者一周前后两次运用龙舟测功仪进行临界功率方法测试,根据本模型中各函数变量所代表的意义的不同,来区分运动员临界功率值和无氧工作能力的强弱,线性模型在Y轴上的起始点的截距代表了运动员的有氧工作能力,函数的斜率代表了运动员的无氧工作能力,可以根据模型判定龙舟运动员训练前后有氧和无氧代谢能力变化的比例大小,在实际训练中,据此进行针对性的训练。
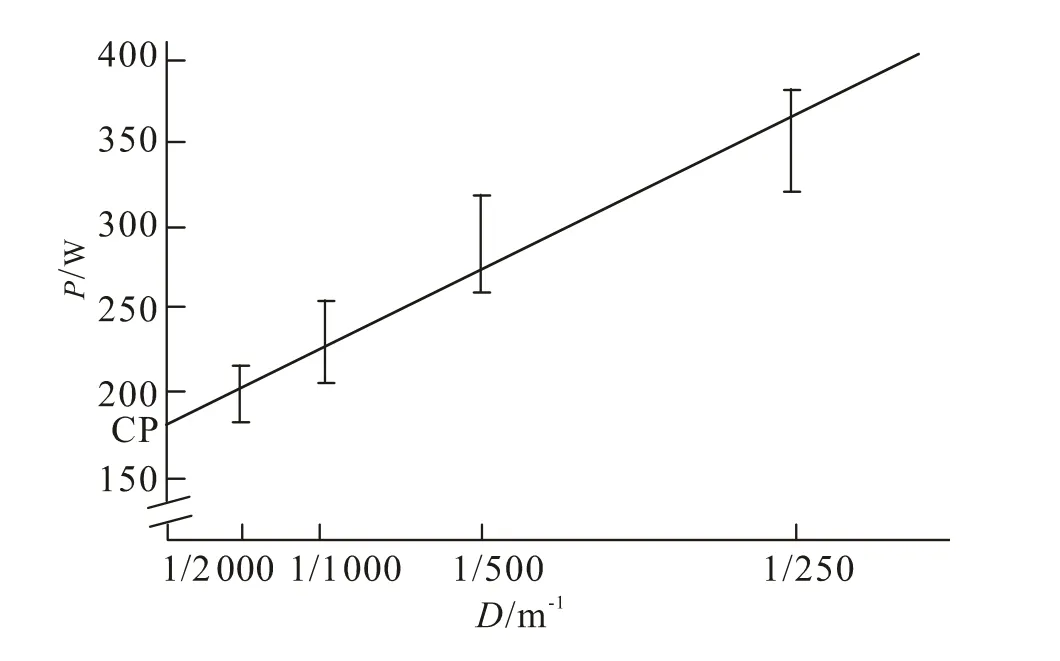
图4 P-D -1模型
从250~2 000 m在龙舟测功仪上测试的运动时间和平均功率变化可以看出:随着设定距离的延长,运动时间明显逐渐延长,而平均功率则明显下降,其生理生化机制与人体磷酸原、糖酵解、有氧代谢3大供能系统在不同时段供能地位的变化有直接关系。从表1可以看出,250~2 000 m的全力运动,平均运动时间50.30~547.83 s,平均功率从342.90 W降至128.43 W,无论从供能时间,还是功率变化特点均证明了供能顺序是从磷酸原→糖酵解→有氧代谢供能的过程,是一个由无氧代谢供能为主向有氧代谢供能为主的渐变过程。从本质上讲,本研究实验方案中的4次测试的目的就是用抽样的方法对这一过程进行数学上的描述,这也正是临界功率测试理论能在各种体能类运动项目应用的核心思想,只是在运动形式、测试方案及评价模型的设计上更适合于专项而已,即通过合理选择几个时间或距离的专项全力运动就可以建立由无氧和有氧能力共同决定的个体体能结构的模型,从而对运动员有氧、无氧代谢能力能够同时完整评价。
本研究对龙舟项目建立临界功率模型时的血乳酸和心率变化特点做了初步研究:表1显示,4次不同距离全力运动后即刻心率的变化特点是逐次升高的(除1 000 m略有下降外),说明从250~2 000 m的运动,运动负荷量增大的结果使机体心血管应激水平逐渐增加,心脏泵血功能增强,血液循环加快,适应了运动时供能和排泄废物的需要。本研究测试结果4次运动后即刻心率值的变化趋势相当于从氧利用能力训练到氧运输能力训练的心率变化范围,这与实验中时间、平均功率变化所描述的代谢供能系统变化规律是一致的。
根据临界功率理论和有关应用研究[11]及本研究结果,提出龙舟运动训练中进行体能评价主要存在以下6种基本情况:1)有氧代谢能力提高,无氧代谢能力提高;2)有氧代谢能力提高,无氧代谢能力不变;3)有氧代谢能力提高,无氧代谢能力下降;4)有氧代谢能力下降,无氧代谢能力提高;5)有氧代谢能力下降,无氧代谢能力不变;6)有氧代谢能力下降,无氧代谢能力下降。
总之,人体内代谢过程是相互联系、相互制约、相互调节的统一连续过程,无论从运动时间、平均功率变化特点,还是即刻心率和血乳酸变化特点来看,本研究在龙舟测功仪上进行 4个设定距离的全力运动,主要获取了龙舟运动员个体从短时间(无氧)到长时间(有氧)代谢能力的信息,通过回归方程(数学模型)的建立,能够完整地描述人体的体能结构,起到评定体能的作用。
通过对龙舟运动员测功仪的测试数据的分析,初步确立了4类数据之间的相关模型。可以运用临界功率的方法和手段对龙舟项目进行评定。其中,龙舟运动员“P-D-1模型”及评价方法是一种比较可靠的方法。
[1] 李兵. 中国龙舟训练科研基地建设与发展探索[J].东北电力大学学报,2010(5):89-92.
[2] 吴昊,冯美云. 赛艇运动员临界功率测试的建立及心率、血乳酸的变化特点初探[J]. 北京体育大学学报,1999,22(3):35-39.
[3] Scherrer J,Monod H L. Le travail musculaire local etla fatigue chezl’homme[J]. J Physio1,1960,52(2):420.
[4] 董德龙,王卫星,范安辉,等. 临界功率(CP):释义与应用[J]. 体育科学,2009,29(6):77-85.
[5] Housh T J,Johson G O. Responses at the fatigue threshold[J]. Physio-Int J Sport Med,1991,12(3):305-308.
[6] Hopkins W G,Edmud I M,Hamilton B H,et al.Re-lation between power and endurance for treadmill running of short duration[J]. Ergonomics,1989,32(12):1565-1571.
[7] Hill D W,Smith J C. Methodologi-cal considera inns in estimation of the power-timerelationship[J]. Med Sci Sport Exe,1994.
[8] Hill D W,Smith J C. Determination of critical power bypulmonary gas exchange[J]. Appl Physiol,1999,24(1):74-86.
[9] Hagerman,S CHERRER J. The work capacity of amuscular group[J]. Ergonomics,1965,8(3):329-338.
[10] Jones G,Swain A B,Hardy L. Intensity and direction di-mensions of rnmpetitive state anxiety and relationships with performance[J]. J Sport Sci,1993,11(6):525-532.
[11] Wakayoshi,Dangelmaier B S,Hill D W. Critical power is related to cycling time trial performance[J]. Int J Sport Med,1999,20(6):374-378.
An application of the critical power theory in dragon boat training
FANG Zhi-jun1,LI Bing2
(1.School of Physical Education,Northeast Normal University,Changchun 130024,China;
2.School of Physical Education,Northeast Dianli University,Changchun 132012,China)
By applying the critical power theory, coupled with the characteristics of energy supply by dragon boat event players at different distances, the authors probed into means to train the physical capacity of the players by applying a dragon boat dynamometer, established mathematical modelsP t,D-t,D-PandP-D-1for dragon boat players, found intervals for critical power training at different distances, and revealed the following findings: 1)model P-tis nonlinear; the curve bottom is close to the critical power point; 2) modelD-tis linear; the slope of the straight line represents the critical power value; 3) modelD-Pis nonlinear; the critical power value (CP) is the point of intersection of a asymptote of this hyperbola function and the power (horizontal axis); 4) modelP-D-1is linear;the intercept represents the aerobic working ability of the players, while the slope of the function represents the anaerobic working ability of the players.
sports training;dragon boat;critical power
G808
A
1006-7116(2012)02-0120-04
2011-06-09
方志军(1956-),男,教授,硕士,研究方向:体育教学与训练。
