开孔矩形腔中场分布的数据模型化初步研究

李 磊，赵 翔，闫丽萍，周海京，黄卡玛

（1．四川大学电子信息学院，四川成都 610064；2．北京应用物理与计算数学研究所，北京 100088）

开孔矩形腔中场分布的数据模型化初步研究

李 磊1，赵 翔1，闫丽萍1，周海京2，黄卡玛1

（1．四川大学电子信息学院，四川成都 610064；2．北京应用物理与计算数学研究所，北京 100088）

为快速估算开孔矩形腔中的电磁场分布，本文提出一种数据模型化方法，对开孔矩形腔的全波分析数据结果进行模型化处理，即通过提取腔内场分布数据的特征参数，来重建场分布情况的原貌。计算实例表明，该方法的预测结果和全波分析结果吻合较好。该方法虽然是基于全波分析计算所得数据，但这些数据的计算过程可以预先进行，因此场分布数据的重建时间可以做到非常短。

开孔矩形腔；数据模型化；全波分析；特征参数

许多电子、电气设备的金属外壳上都含有各种孔缝，用于通风或与外界进行能量／信号的交换。这些孔缝的存在使得有意或无意的外部电磁干扰能藉此进入电子系统，并在其内部的电子元器件上产生感应电流或电压，从而可能对电子系统的正常工作状态产生干扰［1－2］。由于矩形腔体最为常见，因此研究开孔矩形腔中的电磁场分布对电磁兼容设计和电磁效应评估具有重要的指导意义。计算开孔矩形腔中电磁场分布的数值计算方法包括传输线模型分析法［3－4］、时域有限差分法［5］、矩量法［6］、有限元法［7］及联合频域的混合技术等等。虽然这些方法可以较精确地计算外部电磁场耦合到复杂结构模型中的电磁场分布，但电大尺寸带来的巨大计算量和存储量使分析过程变得相当困难［8］，而分析产生的数据结果也会因为数据量太大而无法被恰当地记录下来，以使得数据能被再次使用。同时，一些基于模式分析的方法速度较快，但由于只考虑了单一模式，使得对电大多模腔的分析会产生较大误差［2］。

为此，本文提出一种数据模型化方法，对开孔矩形腔的全波分析数据结果进行模型化处理，即通过提取腔内场分布数据的特征参数，来试图重现场分布情况的原貌。这实际上构成了一种快速估算开孔矩形腔中电磁场分布的新方法。该方法虽然是基于全波分析计算所得数据，但这些数据的计算过程可以预先进行，因此场分布数据的重建时间可以做到非常短。

1 数据模型化方法

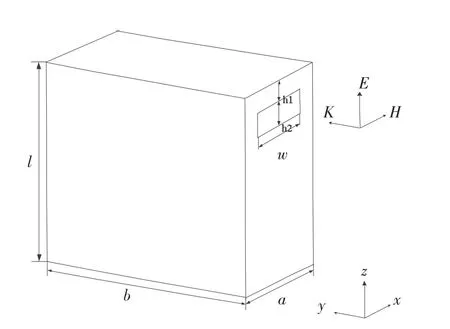
图1 分析模型示意图

以图1所示模型为例介绍数据模型化方法。该模型由一个矩形金属腔体组成，大小和普通计算机主机机箱相近。某侧腔壁上开有如图1所示的一个矩形孔。其中腔体参数为a＝182 mm，b＝420 mm，l＝430 mm，孔缝参数为w＝144 mm，h1＝19 mm，h2＝40 mm。设一均匀平面波垂直入射该矩形腔。

1）最优模式的确定

通过全波仿真软件，对开孔矩形腔中的电磁场分布进行计算，频率范围从1 GHz到15 GHz。在各频率下观察场分布特征，发现与理想矩形腔中场模式分布情况关系密切。以2 GHz时的情况为例，图2给出了电场强度模值在3个横截面（x＝a／2、y＝b／2、z＝l／2）上的分布情况。

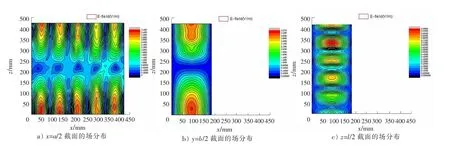
图2 2 GHz时电场强度模值的分布情况

从图2可以看出，一定大小的孔缝对腔体内电磁场分布特征的影响有限，其分布特征和未开孔的矩形谐振腔中特定模式（即“最优模式”）的电磁场分布特征具有较多的相似性。因此，本文首先根据矩形谐振腔各模式的场值计算公式［9］（这里以TM模式为例）：

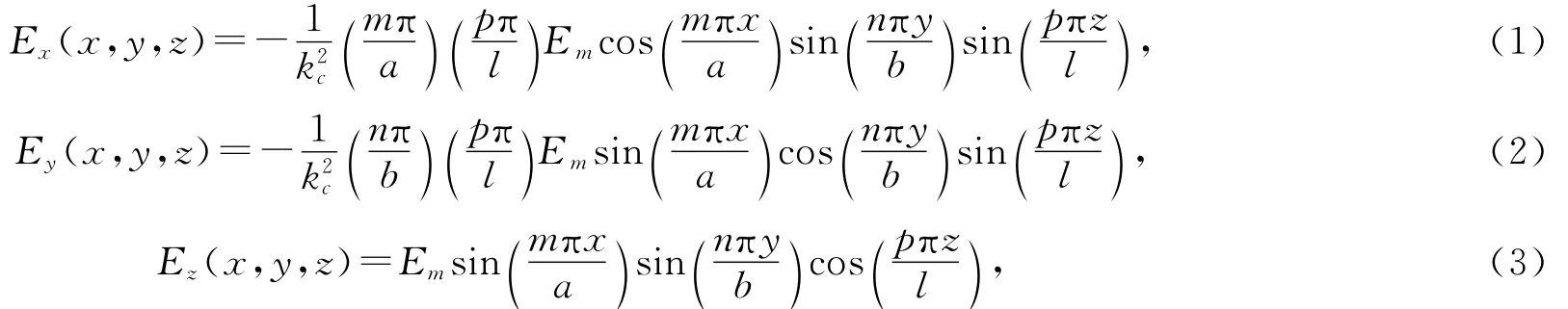
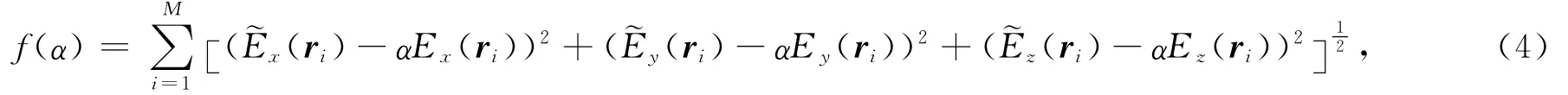
其中M为腔内采样点数目，ri＝（xi，yi，zi）为采样点坐标，（˜Ex，˜Ey，˜Ez）为全波分析算出的在某点处的电场强度，（Ex，Ey，Ez）为某模式在相同点处的电场强度，α为模式权重系数。通过比较不同模式拟合后的最优目标值来确定最优模式。拟合结果表明本例中的最优模式为TM151。

2）特征参数的提取

接下来对全波分析获得的场分布数据进行特征参数的提取。这些特征参数可以是腔体内电磁场量的均值、方差和最大值等等。

下面介绍将场值的区域最大值作为特征参数的情况。首先，根据TM151模式的场结构特征将腔内区域均分为10个子区域，上、下各5个子区域。然后，求出这10个子区域中各自的全波分析结果最大值˜Emaxi（i＝1，2，…，10）和TM151模式下的最大值Emaxi（i＝1，2，…，10），并由此得到对应子区域的两个最大值之比vi。

采用数据拟合的方法在若干模式中找出该最优模式。本文通过最小化如下目标函数来进行数据拟合：

最后将该比值vi记为该子区域的特征参数。表1是本例中提取的10个特征参数。

表1 提取的10个子区域的特征参数

这些特征参数通过对最优模式的场分布函数进行微扰，来重建开孔矩形腔中的场分布。一种较为简单的处理方法是，开孔矩形腔中任意位置处的场值用最优模式在该位置的场值乘以该位置所在子区域的特征参数来得到。

2 算例与结果

基于上述方法，对开孔腔体内的电磁场分布进行了部分频率的预测（重建）。图3给出了2 GHz时的预测结果。比较图2和图3可知，在x＝a／2和y＝b／2截面，预测和仿真的腔体内的电磁场分布比较吻合，幅度也保持一致，但是在z＝l／2截面，预测结果的相对误差较前两者稍大，这是因为该截面所处区域的场值整体都很小。

3 结 语

为快速估算开孔矩形腔中的电磁场分布，笔者提出一种数据模型化方法，对开孔矩形腔的全波分析数据结果进行模型化处理，即通过提取腔内场分布数据的特征参数，来重建场分布情况的原貌。计算实例表明，该方法的预测结果和全波分析结果吻合较好。该方法虽然是基于全波分析计算所得数据，但这些数据的计算过程可以预先进行，因此场分布数据的重建时间可以做到非常短。

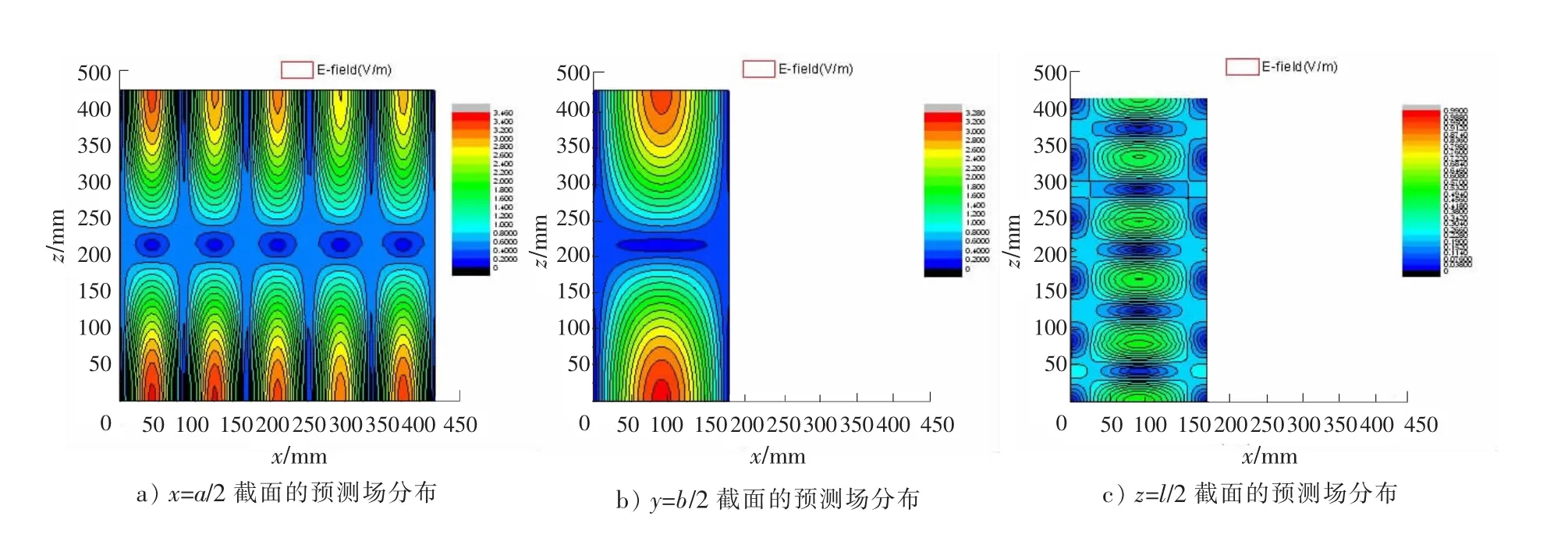
图3 2 GHz时腔内场分布的预测结果

［1］ BUTLER C M，RAHMAT－SAMII Y，MITTRA R．Electromagnetic penetration through apertures in conducting surfaces［J］．IEEE Trans Antennas Propagat，1978，26：291－302．

［2］ LIANG C H，CHENG D K．Electromagnetic fields coupled into a cavity with a slot－aperture under resonant conditions［J］．IEEE Trans Antennas Propagat，1982，30：664－672．

［3］ CHRISTOPOULOS C．Application of the TLM method to equipment shielding problems［J］．IEEE Int Symp Electromagnetic Compatibility，1998，10：188－193．

［4］ RENDER M C，MARVIN A C．Amultiple mode equivalent transmission line method of crosstalk between conductors in shielded environments［J］．IEEE Trans Electromagn Compat，1995，37（3）：488－494．

［5］ MIX J，HAUSSMANN G，PIKET－MAY M，et al．EMC／EMI design and analysis using FDTD［J］．IEEE Int Symp Electromagnetic Compatibility，1998，10：177－181．

［6］ HARRINGTON R F，MAUTZ J R．Characteristic modes for aperture problems［J］．IEEE Trans Microw Theory Tech，1985，33（6）：500－505．

［7］ VOLAKIS J L，CHATTERJEE A，KEMPEL L C．Finite element method for electromagnetics［M］．New York：IEEE Press，1998．

［8］ GEORGAKOPOULOS S V，BIRTCHER C R，BALANIS A．HIRF penetration through apertures：FDTD versus measurements［J］．IEEE Trans Electromagn Compat，2001，43（3）：282－294．

［9］ 谢处方，饶克谨．电磁场与电磁波［M］．北京，高等教育出版社，2005．

O451

A

1008－1542（2011）12－0162－03

2011－06－20；责任编辑：王士忠

李 磊（1986－），男，河南周口人，硕士研究生，主要从事电磁兼容方面的研究。