集成电路方波注入损伤效应试验研究

曹艳宾，武占成，孙永卫，高永生，李鹏举

（军械工程学院静电与电磁防护研究所，河北石家庄 050003）

集成电路方波注入损伤效应试验研究

曹艳宾，武占成，孙永卫，高永生，李鹏举

（军械工程学院静电与电磁防护研究所，河北石家庄 050003）

为了准确测试方波脉冲注入对集成电路的影响，本文对GJB 538－88中的方波注入法进行了改进，通过设计专用测试夹具，解决了方波产生的辐射场及其高频反射对测试结果的影响，建立了由高频脉冲模拟器、专用测试夹具和示波器等组成的测试系统。利用该系统测试了74LS08的性能参数。

方波注入；集成电路；损伤效应

对电子器件损伤阈值的确定，主要以测定器件的损伤功率值为主，采用方波脉冲注入的电过应力法，选择个别脉宽进行实验得到。现在方波注入试验是按照GJB 538—88［1］中的相关说明进行的，但是GJB 538－88中没有考虑方波产生的辐射场及其高频反射对测试结果的影响。因此，通过采用专门的测试夹具来改善试验条件，并用改进的测试系统对集成电路74LS08进行方波注入试验，得到74LS08损伤参数随脉宽变化的规律。

1 集成电路方波注入测试系统

1．1 试验方法及装置

图1为建立的集成电路方波注入测试系统示意图，选择器件为74LS08（四重2输入与门），注入端对选择“输入－地”端。试验仪器包括：高频噪声发生器；同轴线；测试夹具；脉冲衰减器；示波器；万用表以及器件在线测试仪等。高频噪声发生器产生脉宽和幅值可调的方波，经过同轴线传输施加在固定在测试夹具上的器件上。器件两端的电压值（即夹具两端的电压值）经衰减器后显示在示波器上。采样电阻与器件串联在一起，测量采样电阻两端的电压，即可计算出流经器件上的电流值。由示波器记录电压、电流波形并计算功率和能量。由器件在线测试仪记录首次注入前及每次注入后器件各端对之间的U－I曲线，并将二者作比较。如检测出有超差曲线出现，说明器件已经发生损伤；如在所设置的误差范围内无超差曲线出现，则继续实验，直到器件发生损伤为止。为了满足测试系统的阻抗匹配的要求，图1中的仪器及传输线的特性阻抗都是50Ω。用万用表测量损伤前后“输入－地”端的电阻变化。系统中使用的方波源为ISN－4040高频噪声模拟发生器，示波器为7154B型示波器。采样电阻选择阻值1Ω、最大功率为10 W的无感电阻。

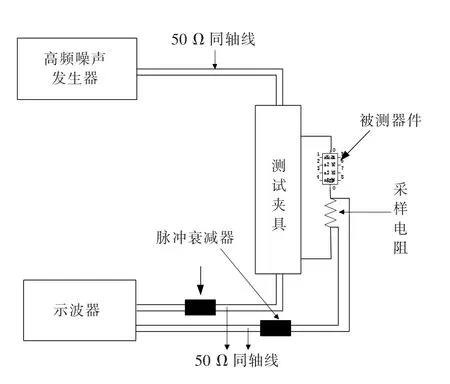
图1 集成电路方波注入测试系统示意图

1．2 测试夹具的研制

该测试系统中基于微带设计原理和电磁场屏蔽理论研制了专用测试夹具。

微带线的基本结构如图2所示，在高频介质基片上，一面全部敷上导电层（即接地板），另一面敷上带状导电层（导体带）。

微带线的特性阻抗Z0是由微带线的几何尺寸、介质参数等决定的。Z0可由式（1）求得。

对于W／h≤1的窄带情况，有：

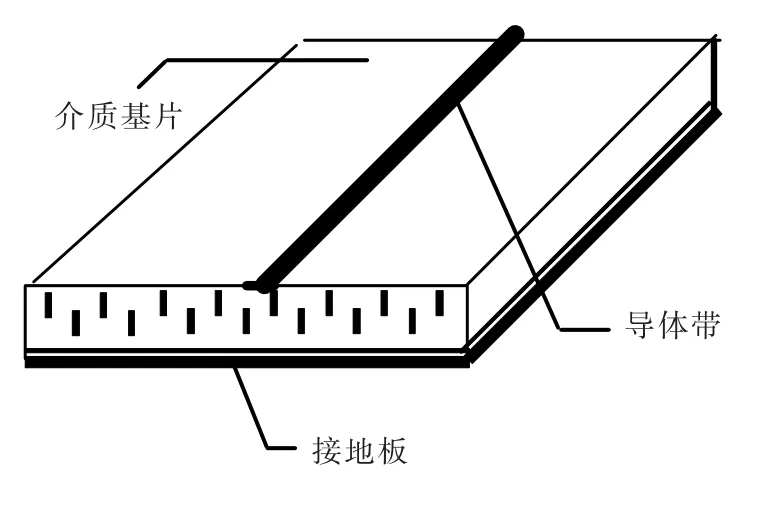
图2 微带线的基本结构

式中：W为金属导体带条宽度；h为基材介质的厚度；εr为基材的相对介电常数；εeff为基材介质的有效介质常数。

利用上述式（3）和式（4），已知εr，W／h，通过求得εeff，可以计算出微带线特性阻抗Z0；反之，已知特性阻抗Z0和基片介电常数εr，可算出微带线宽高比，进而得出微带线的几何尺寸。

同样，微带线的工作频率也受到限制，具体可以由下列公式表示：

根据微带线参数和公式（6），可以计算出微带线夹具的工作截止频率。

综合考虑各项因素，选择环氧树脂为基片介质，选择铜为导体带材料时可满足方波注入的测试要求。环氧树脂的相对介电常数εr＝4．9，介质基片厚度h＝1．5 mm，微带特性阻抗Z0＝50Ω，根据上述公式，计算得：W／h＝2．51，微带线导体带宽度W≈3．76 mm，微带线的工作截止频率约为35．78 GHz。

测试夹具的实物图如图3所示。

利用安捷伦N5230A型矢量网络分析仪，对该测试夹具测试的传输特性进行了测试，测试结果如图4所示。从图4中可以看出该测试夹具在0～6 GHz之间具有较好的传输特性，仅1．32，1．85，3．7，5．12 GHz 4个频率时出现了较大的衰减，且最大衰减倍数为7．022 9 dB。

图3 测试夹具实物图

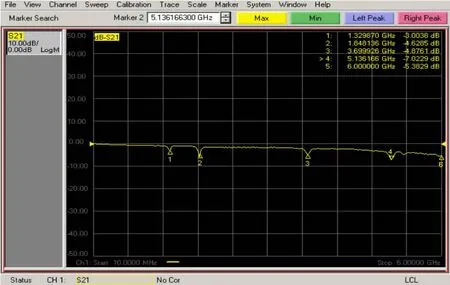
图4 测试夹具传输特性测试图

2 试验结果

2．1 响应电压与注入电压的关系

试验注入电压与器件实际响应的峰值电压是不同的，器件响应的峰值电压小于注入电压幅值。对74LS08器件的分析表明，在未损伤前它的峰值电压与注入电压的关系可以表示为简单的线性函数关系，即y＝kx＋y0，如图5所示。但在发生损伤那一刻，响应电压急剧下降，响应电流却急剧上升。从图6中可以看到，当方波脉冲刚注入时，响应电压值很大，而电流值很小，电压开始下降的时候，电流突然上升，达到注入脉冲宽度时，电流又突然下降。从试验现象上分析，与典型的热二次击穿相似［2］。

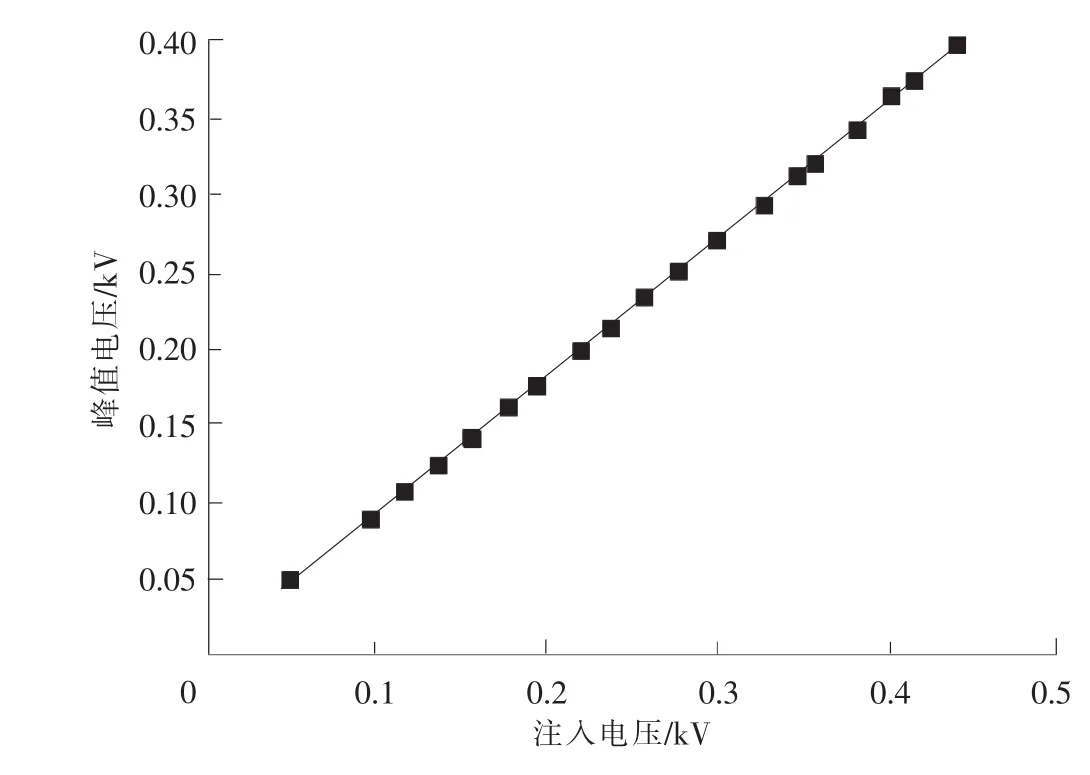
图5 响应电压与注入电压关系图（t＝100 ns）

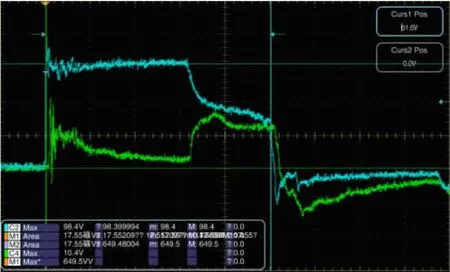
图6 74LS08损伤时电压与电流波形图

2．2 功率（能量）与注入电压的关系

采用器件损伤时的注入电压作为器件的损伤电压阈值，器件在损伤时实际吸收的功率（能量）作为器件的损伤功率（能量）阈值。

图7为74LS08器件的注入电压与平均功率的数据散点图和曲线拟合关系图。拟合结果表明，对平均功率与注入电压之间的关系采用函数y＝axb来拟合，取得了非常高的精度（R2近似等于1）。说明此函数能够很好地表示注入电压与功率间的关系。

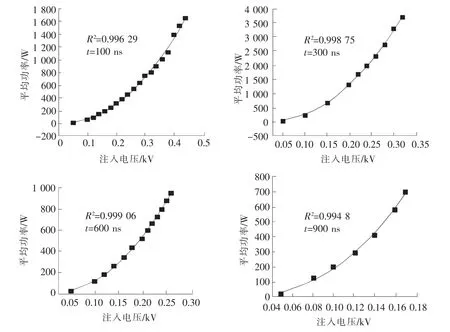
图7 不同脉宽条件下功率与注入电压的拟合关系曲线

从拟合结果看出，在不同脉宽注入条件下，函数关系式y＝axb可以比较准确地表示平均功率与注入电压的关系。且这种关系在不同脉宽注入条件下均存在，相关度很高。

2．3 损伤电压与脉宽的关系

由于损伤电压与功率（能量）阈值存在一定的函数关系，如果能够确定损伤电压与脉宽之间的函数关系，就有可能建立器件的损伤模型，为此对器件不同脉宽下的损伤电压值进行了研究。图8为74LS08损伤电压（损伤时的方波幅值）与注入脉宽实验数据散点图。

74LS08的损伤电压值随着注入脉宽的变化而变化。脉宽越大，损伤电压越低；脉宽越小，损伤电压值越高，这说明对于74LS08器件，致其损伤的主要因素不是电压，而是功率或能量。根据散点图分布趋势，采用y＝ax－b函数对数据点进行拟合，拟合精度较高（R2＝0．996 07）。而且，注入脉宽越小曲线下降越快，当注入脉宽大于800 ns时曲线下降趋势变缓。

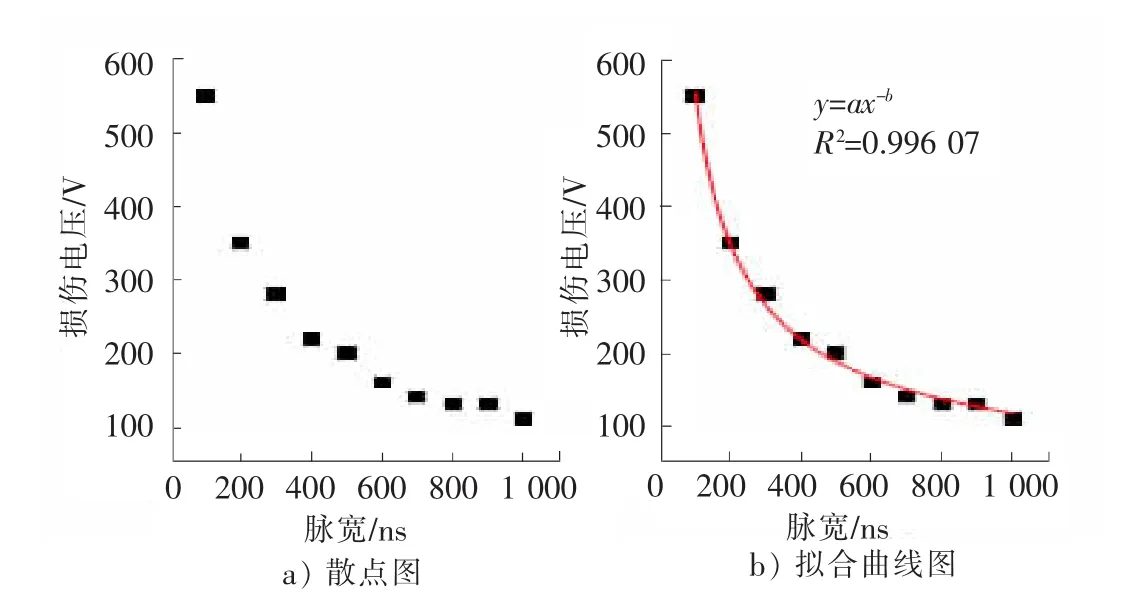
图8 74LS08损伤电压与脉宽关系图

3 结 语

通过设计专用的测试夹具对GJB 538－88中的方波注入法进行了改进，解决了方波产生的辐射场及其高频反射对测试结果的影响，建立了由高频脉冲模拟器、专用测试夹具和示波器等组成的测试系统。利用该系统对74LS08的性能参数进行测试，得出了74LS08的响应电压与注入电压之间呈简单的线性函数关系：y＝kx＋y0；功率（能量）与注入电压之间呈非线性关系：y＝axb，且在不同的脉宽注入条件下均存在；损伤电压与脉宽之间呈非线性关系：y＝ax－b，且注入脉宽越小曲线下降越快，大于800 ns时曲线下降趋势变缓。

［1］ GJB 538—88，半导体器件的电磁脉冲损伤阈值实验方法［S］．

［2］ 张希军，范丽思，王振兴，等．静电放电保护器件性能测试技术研究［J］．河北大学学报（自然科学版），2010，30（5）：609－612．

O411．1

A

1008－1542（2011）12－0129－04

2011－06－20；责任编辑：李 穆

曹艳宾（1983－），男，河北衡水人，工程师，主要从事电磁兼容方面的研究。