含有微孔的超弹性球体的径向增长问题

高 洋，韦 涛

(大连民族学院理学院学生辽宁大连 116605)

含有微孔的超弹性球体的径向增长问题

高 洋，韦 涛

(大连民族学院理学院学生辽宁大连 116605)

橡胶和类橡胶材料及其制品在现实生活中的应用非常广泛，在使用过程中都会遇到变形、失稳、使用寿命有限以及破坏等问题，使得相关问题的研究一直是人们关注的焦点。从力学性能上讲，这些材料属于典型的非线性弹性材料范畴。关于这些材料和结构的有限变形问题的数学模型可归结为非线性微分方程的初边值问题。专著［1］和文献［2］对非线性弹性材料和结构的有限变形问题和空穴问题的研究进展进行了详实的综述。相关的文献还可参见文献［3－6］。本文研究了由不可压缩非线性弹性材料组成的含有微孔的球体在外表面受拉状态下的有限变形问题，利用最小势能原理求得了描述拉伸载荷与微孔增长之间关系的表达式，同时给出了相应的数值算例，并讨论了材料参数和结构参数对微孔增长的影响。

1 数学模型的建立及其解

考察一个由不可压的非线性弹性材料组成的含有微孔的球体在外表面均布的径向拉伸载荷p0作用下的球对称变形问题。在球坐标系下，取球壳变形前后的球坐标分别为(R，Θ，Φ)和(r，θ，φ)，球壳所占区域为其中:a和b分别为球体变形前的微孔半径和外半径;r(R)是待定的径向变形函数。在球对称变形的假设下，变形梯度张量F的主伸长λi(i=1，2，3)分别为其中c≥a是一个积分常数，它描述了含有微孔的球体变形后的径向增长量。

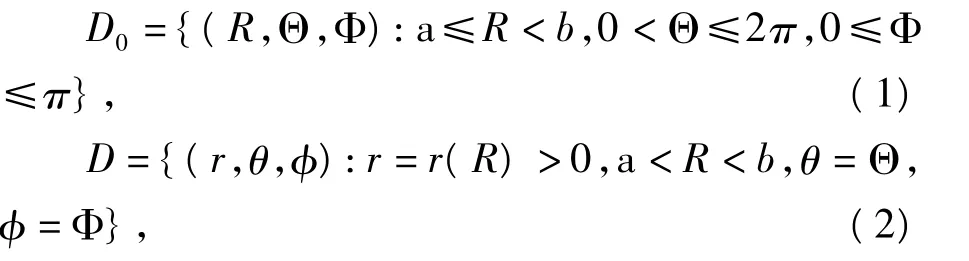
对应于球体内部空穴半径为a的任意构形的总能量为

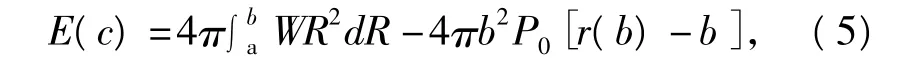
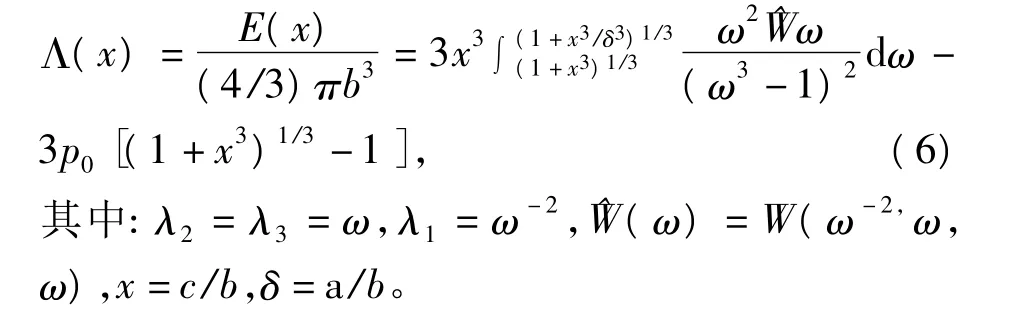
由于球体受到拉伸载荷的作用，根据最小势能原理，球体可能的平衡位置可由Λ'(x)=0得到。经化简可得其中:W=W(λ1，λ2，λ3)是不可压缩非线性弹性材料的应变能函数。式(4)中的第一项是总的应变能，第二项表示外表面拉伸载荷所做的功。将式(3)和(4)代入到式(5)，并将其无量纲化，得到

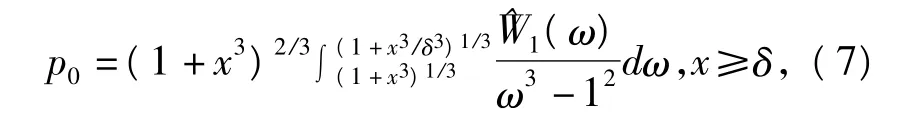
式(7)描述了不可压缩非线性弹性材料组成的含有微孔的球体在外表面拉伸载荷p0作用下，微孔增长p0与之间的精确关系。然而对于不同的不可压缩非线性弹性材料，微孔的增长的情况也不尽相同。

2 数值算例

本文考虑不可压缩Gent－Thomas材料，对应的应变能函数为其中μ1，μ2是材料的无穷小变形的剪切模量。此

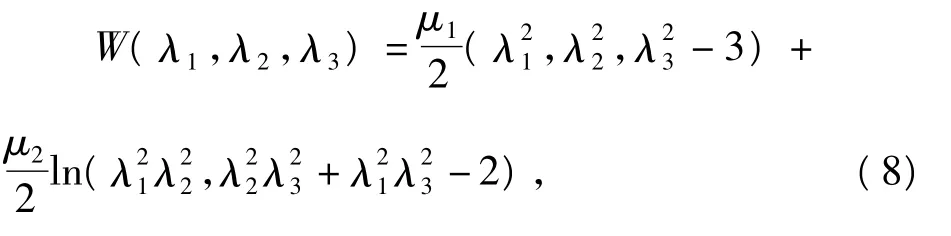
图1 材料参数α取相对较小值时微孔半径与拉伸载荷之间的增长关系，α=1。

由图1可见，对于给定的材料参数和结构参数，当初始微孔半径较小时，随着拉伸载荷的增加，微孔增长得很慢，当载荷达到一定值时，微孔会突然增长;当初始微孔半径相对较大时，随着拉伸载荷的增加，微孔的增长会趋于平缓。

由图2可见，对于给定的材料参数和结构参数，参数存在一个临界值，当时，随着拉伸载荷的增加，微孔的增长会趋于平缓;然而，当时，随着拉伸载荷的增加，微孔半径会出现跳跃性增长(这种现象可以用最小势能原理来进行解释)。

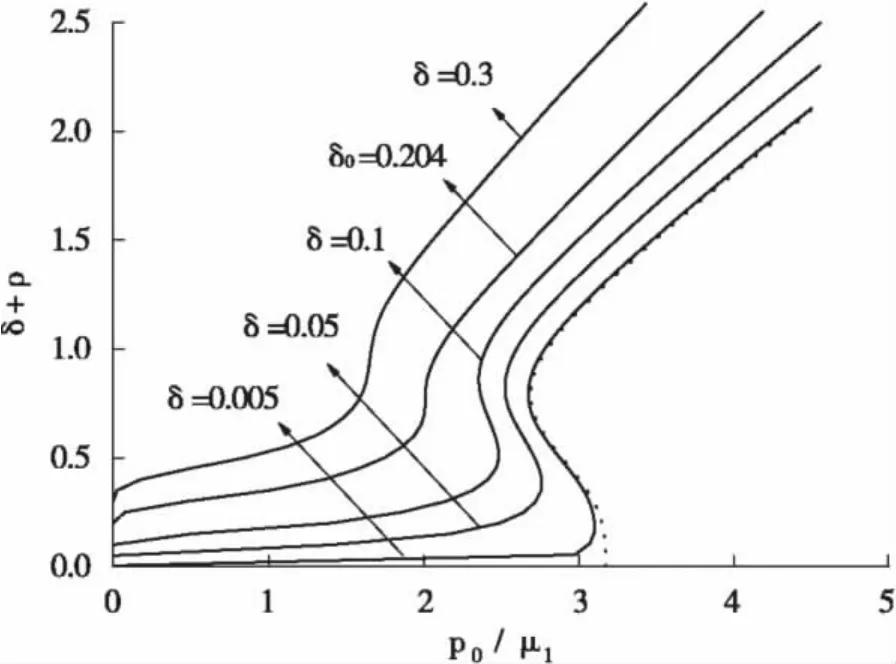
图2 材料参数α取相对较大值时微孔半径与拉伸载荷之间的增长关系，α=3。

［1］FU Y B，OGDEN R W.Nonlinear Elasticity:Theory and Applications［M］.London Math.Society Lecture Note Series 2001.

［2］POLIGNONE D A，HORGAN C O.Cavitation for incompressible anisotropic nonlinearly elastic spheres［J］.外应变能函数(8)也可记为对于不同的材料参数，载荷与微孔半径的增长关系如下图所示:Journal of Elasticity，1993，33(1):27–65.

［3］ YUAN Xuegang，ZHU Zhengyou，CHENG Changjun.Study on cavitated bifurcation problem for spheres composed of hyper－elastic materials［J］.Journal of Engineering Mathematics，2005，51(1):15－34.

［4］袁学刚.关于超弹性材料球体中空穴分岔问题的研究(Ⅰ)［J］.烟台大学学报(自然科学版)，2005，18(2):79－90.

［5］REN Jiusheng，YUAN Xuegang.Mechanics of formation and rupture of human aneurysm ［J］.Applied Mathematics and Mechanics(English Edition)，2010，31(5):593－604.

［6］NIU Datian，ZHANG You，YUAN Xuegang，et al.Analytic Solutions of Parametric Type and Numerical Simulations of a Class of Nonlinear Ordinary Differential Equations［J］.Applied Mathematical Sciences，2010，4(30):1451－1455.

0343

A

1009－315X(2011)05－0530－02

2010－12－07;最后

2011－07－26

国家自然科学基金(10872045)。

指导教师:袁学刚(1971－)，男，吉林桦甸人，教授，博士，学校优秀学术带头人，主要从事数值逼近和非线性微分方程的解法等研究。

(责任编辑 刘敏)