基于波概念迭代法的缝隙加载H形双频天线分析

姬五胜，罗全珍，杨 帆，李益敏，张 妍

（1.兰州城市学院电子信息科学与技术研究所，甘肃兰州 730070；2.西安电子科技大学电子工程学院，陕西西安 710071；3.兰州理工大学计算机与通信学院，甘肃兰州 730050）

基于波概念迭代法的缝隙加载H形双频天线分析

姬五胜1，2，罗全珍3，杨 帆3，李益敏3，张 妍1

（1.兰州城市学院电子信息科学与技术研究所，甘肃兰州 730070；2.西安电子科技大学电子工程学院，陕西西安 710071；3.兰州理工大学计算机与通信学院，甘肃兰州 730050）

阐述了波概念迭代法的基本原理，描述了同轴探针激励条件下空域散射算子的表达形式，运用WCIP方法仿真了缝隙加载H形双频天线表面的电场和电流密度分布，分析了该天线的回波损耗，计算结果与参考结论进行了对比，达到了较好的一致性，从而验证该方法的正确性和有效性。

微带天线；波概念迭代法；傅里叶模式变换；回波损耗

微带天线具有剖面薄、体积小、质量轻、便于集成等优点，广泛应用于移动通信、航空航天、卫星通信等领域［1］，而具有双频（或多频）特性的微带天线是近年来的研究热点之一［2］。分析该类天线的常用数值计算方法有矩量法、有限差分法、有限元法等，都存在一定的局限性。如矩量法对内部区域建模问题困难大，有限差分法对无边界问题需要吸收边界条件处理，有限元法对无边界问题需要对边界进行建模［3］，同时这些传统的数值计算方法要消耗大量的内存以及计算时间。针对这一问题，1996年，AZIZI等学者提出了波概念迭代法［4］。该方法结合了传输线理论与傅里叶模式变换，通过电路表面的切向电场和电流密度引入波的概念。由于该方法概念新颖、建模简便、计算快捷，得到了快速发展，成功应用于微带天线［5－6］、滤波器［7］等平面微带电路的研究中。

笔者在波概念迭代法的理论基础上，描述了微带结构在同轴探针激励下空域散射算子的表达形式，运用该方法对U形缝隙加载H形双频天线进行分析，通过仿真电路表面的场分布及求解回波损耗验证了该方法的正确性，并与矩量法在计算复杂度方面比较论证了该方法的有效性，从而扩展了该方法的应用范围。

1 原理阐述

波概念迭代法通过电路分界面的切向电场和电流密度引入横向电磁波（图1），波概念定义如下：

其中：Ai是电路交界面的入射波；Bi是反射波，i（i＝1，2）表示界面两侧的不同介质区域；Z0i是介质的特征阻抗，其值为

1.1 空域散射算子

将微带结构的分界面剖分成小矩形网格，则分界面被划分为金属区域、介质区域、源区域以及其他区域，根据各个区域的边界条件得到相应的散射矩阵，从而得到空域散射算子。空域散射算子表征空域入射波和空域反射波之间的关系：

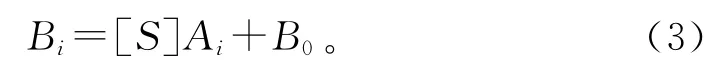
对于金属区域，其边界条件：E1＝E2＝0，介质区域的边界条件：J1＋J2＝0，E1＝E2≠0。将该边界条件分别代入式（1）、式（2），得到金属和介质区域空域入射波与空域反射波之间的关系：

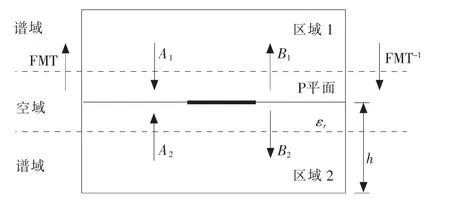
图1 波概念的定义Fig.1 Definition of wave concept

对于源区域，同轴探针经过接地板与分界面的贴片相连，天线由馈电探针与底板之间的电压所激励，其空域入射波与空域反射波之间的关系为

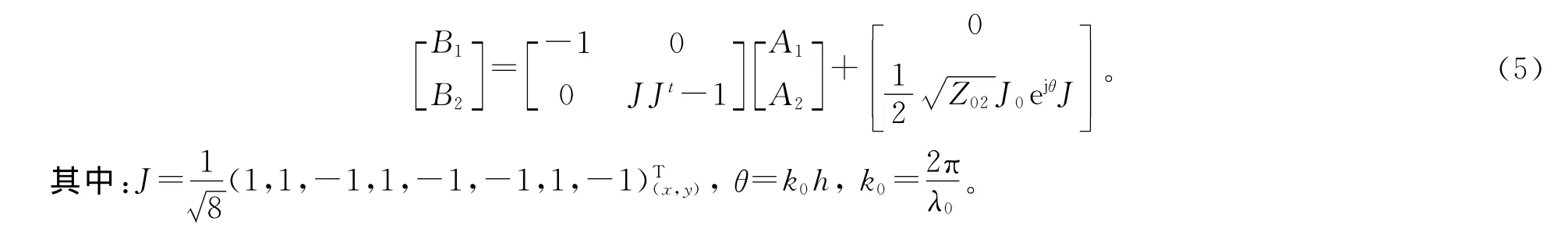
1.2 谱域反射算子

谱域波在上、下区域发生反射。谱域入射波和谱域反射波之间的关系为

谱域反射算子由下式求得：

1.3 傅里叶模式变换

空域波和谱域波之间的转换采用傅里叶模式变换，其变换如下：

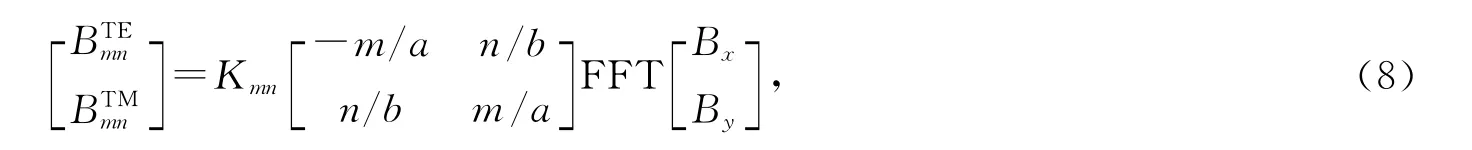
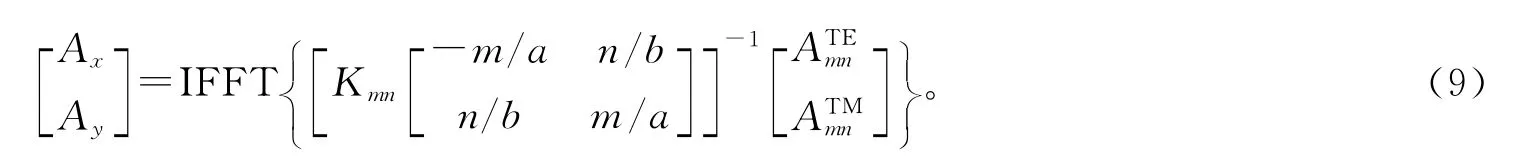
1.4 迭代过程

首先在电路的源区域处给定初始激励，则在电路上、下区域产生空域反射波Bi（i＝1，2）；此时，通过傅里叶模式变换将波转换至谱域，得到谱域入射波；通过谱域反射算子进一步得到谱域反射波；反射后的谱域波经过傅里叶模式反变换得到空域入射波Ai；最后经过空域散射算子再次得到新的空域反射波，完成一次迭代过程。如此反复循环，经过第k次迭代后参数收敛，然后根据第k次的空域波得到切向电场和电流密度，进一步计算得到所需的参数。

2 数值结果

图2是一种U形缝隙加载H形双频天线［2］，该天线由同轴探针馈电，H形结构降低了天线的谐振频率，缩小了天线尺寸，U形缝隙实现了双频效果。其双频效果主要是利用TM10和TM30谐振模式。天线参数如表1所示。

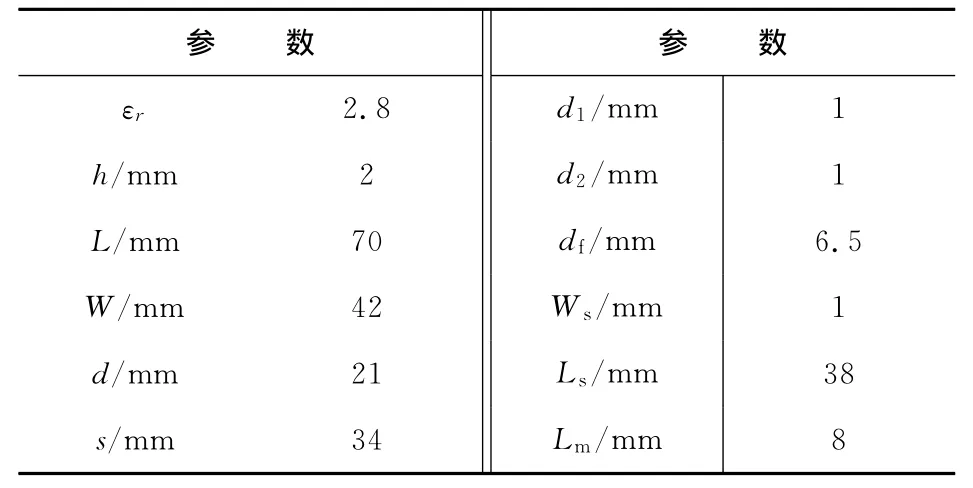
表1 缝隙加载H形天线参数Tab.1 Parameter of slot-loaded H-shaped antenna

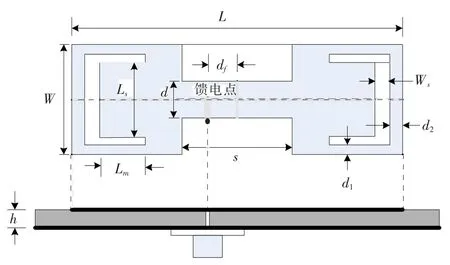
图2 缝隙加载H形天线Fig.2 Slot-loaded H-shaped antenna

用Matlab编写基于WCIP的程序，将缝隙加载H形天线的不连续性表面剖分为140×140个的网格，经过500步迭代运算，得到缝隙加载H形天线表面的电场分布如图3所示，电流密度分布如图4所示。可以看出，天线表面的切向电场在金属区域的值为0，电流密度在介质区域的值为0，满足电路表面的边界条件。图5显示了WCIP方法计算的天线回波损耗与文献参考结论的对比情况，图5中WCIP方法计算得到的谐振频率分别为930 MHz和1 800 MHz，谐振时幅值为－21.8 d B和－18.3 d B，参考谐振频率为929 MHz和1 790 MHz，谐振时幅值为－20 dB和－16.3 dB，结果表明WCIP计算的回波损耗除了曲线走势略有不足外，谐振频率及幅值均吻合很好，从而证明了该方法的正确性。

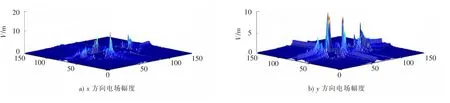
图3 电场分布Fig.3 Electric field distribution

下面对WCIP方法的有效性进行分析，已知WCIP方法的计算复杂度为q（4P＋12P log2P），矩量法的计算复杂度：（KP）3／3。在本例中，电路分界面金属区域占整个表面的比例K＝11%，网格剖分数P＝19 600，迭代次数q＝500，图7显示了波概念迭代法与矩量法的计算复杂度对比，可以看出，波概念迭代法相对于矩量法在分析该电路时有较高的计算效率。

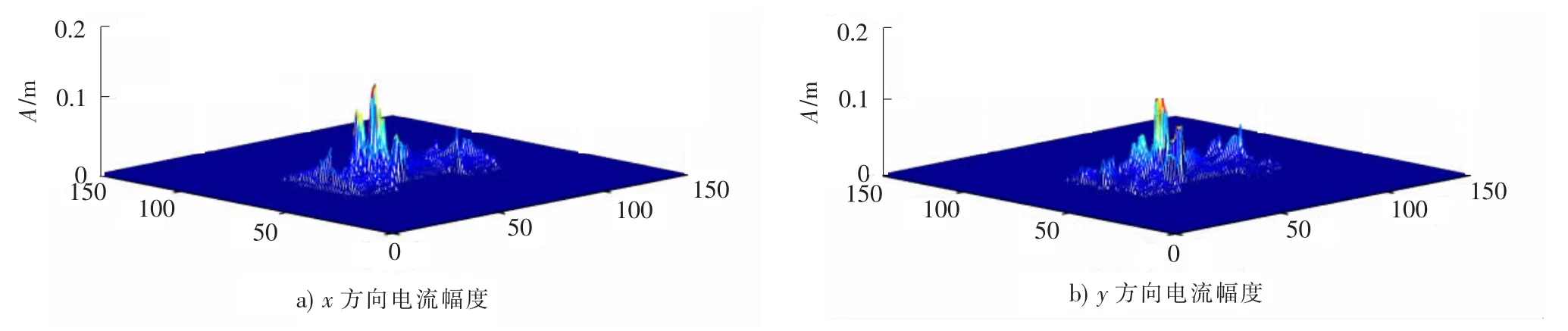
图4 电流密度分布Fig.4 Current density distribution

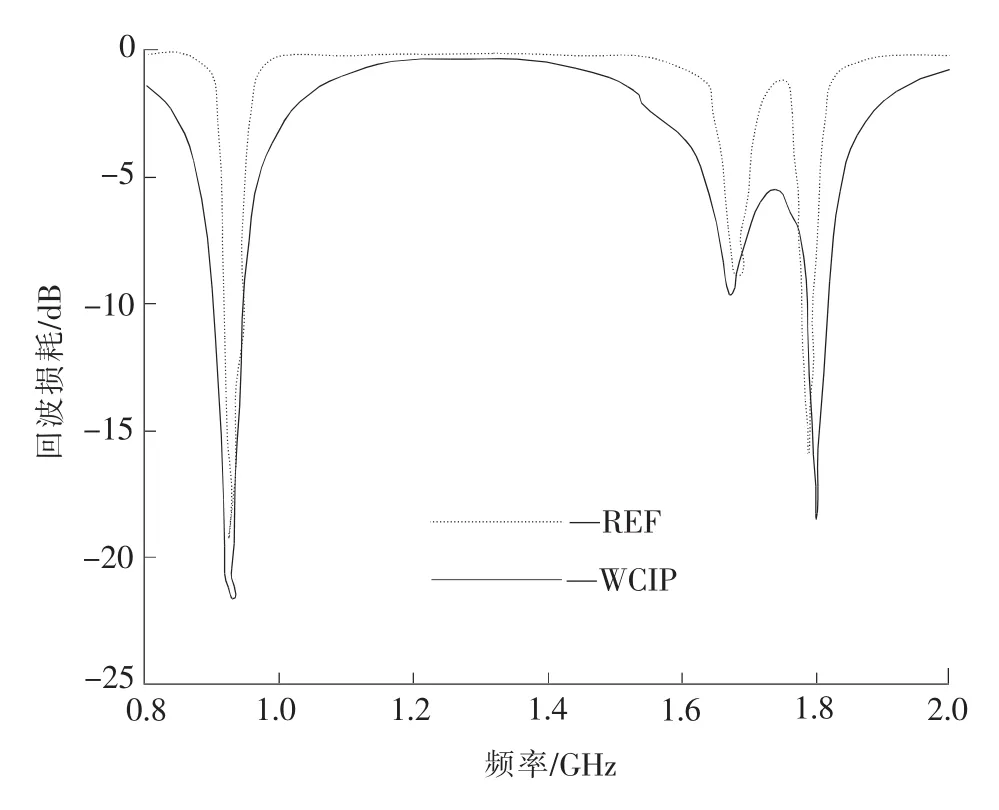
图5 WCIP计算的回波损耗与参考结论对比Fig.5 Comparison of return loss between WCIP and reference data

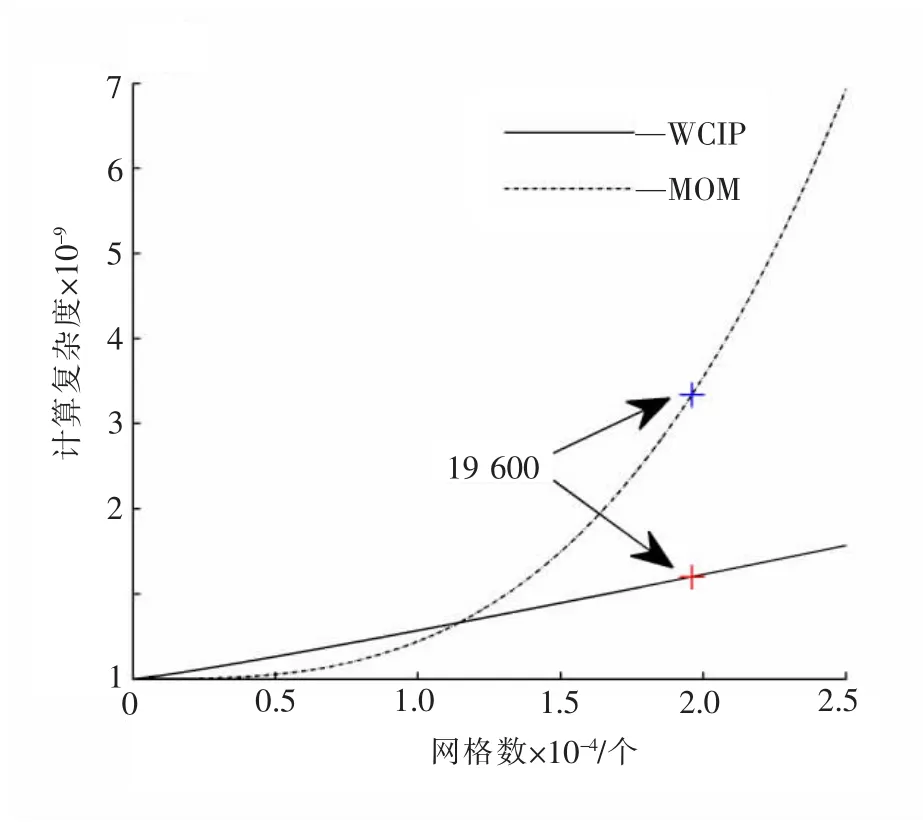
图6 矩量法与波概念迭代法的计算复杂度比较Fig.6 Computational complexity comparison of MOM and WCIP

波概念迭代法在分析微带天线时，只对天线的不连续性表面剖分网格，同轴探针激励处的区域定义为源区域，贴片所在区域为金属区域，其他为介质区域，根据各自区域的边界条件建立空域散射算子，从而表征空域波之间的关系；电路表面之外的区域利用传输线理论等效，电路模型建立简单；利用空域波在分界面的散射和谱域波在上、下区域的反射关系展开迭代运算，避免了基函数的选取和大矩阵的求逆，简化了运算；空域和谱域波之间的交互采用傅里叶模式变换实现，提高了计算速度。本例中，在CPU主频为2 GHz，内存为2 GB的计算条件下，采用Matlab编程对该电路的仿真时间为7′26″。可以看出波概念迭代法特别适合于分析具有分层介质的微波平面电路。

3 小 结

运用了波概念迭代法对缝隙加载H形双频天线进行了研究，仿真了天线表面的电场和电流密度分布，所得结果符合天线的表面边界条件；同时还分析了微带天线的回波损耗，计算结果与参考结论有较好的一致性。结果表明波概念迭代法具有概念清晰、处理简便、计算效率高的优点，由于该方法基于分界面通过电场和电流密度引入入射波和反射波，特别适合微波平面电路研究。

［1］ 钟顺时.微带天线理论与应用［M］.西安：西安电子科技大学出版社，1991.

［2］ 戚冬生，黎滨洪，刘海涛，等.缝隙加载 H 形双频天线［J］.电波科学学报（Chinese Journal of Radio Science），2004，19（1）：95-98.

［3］ 倪光正，杨仕友，钱秀英.工程电磁场数值计算［M］.北京：机械工业出版社，2004.

［4］ AZIZI M，BOUSSOUIS M，AUBERT H，et al.A three-dimensional analysis of planar discontinuities by an iterative method［J］.Microwave and Optical Technology Letters，1996，13（6）：372-376.

［5］ JI W，LUO Q，YANG F.Analysis of H-shaped patch antenna by wave concept iterative procedure（WCIP）［A］.ICMMT 2010 Proceedings［C］.Chengdu：［s.n.］，2010.797-800.

［6］ ZAIRI H，GHARSALLAH A，GHARBI A，et al.Modelisation of probe feed excitation using iterative method［J］.Applied Computational Electromagnetics Society Journal，2004，19（3）：198-205.

［7］ GHARSALLAH A，GHARBI A，DESCLOS L，et al.Analysis of interdigital capacitor and quasi-lumped miniaturized filters using iterative method［J］.International Journal of Numerical Modelling，2002，15（2）：169-179.

Analysis of slot-loaded H-shaped dual-frequency antenna by wave concept iterative procedure

JI Wu-sheng1，2，LUO Quan-zhen3，YANG Fan3，LI Yi-min3，ZHANG Yan1
（1.Institute of Electronic Information Science and Technology，Lanzhou City University，Lanzhou Gansu 730070，China；2.School of Electronic Engineering，Xidian University，Xi＇an Shaanxi 710071，China；3.School of Computer and Communication，Lanzhou University of Technology，Lanzhou Gansu 730050，China）

In this paper，the principle of the wave concept iterative procedure（WCIP）are described.The spatial diffraction operation is concluded in coaxial probe feed conditions.The transverse electric field and current density distribution of slot-loaded H-shaped dual-frequency antenna surface are simulated by the WCIP.Besides，the return loss of the antenna is analyzed.The numerical results show a good agreement compared with the references，which illustrates the correctness and efficiency of the WCIP.

microstrip antenna；WCIP；FMT；return loss

TN828.4

A

1008-1542（2011）05-0451-04

2011-02-22；

2011-07-03；责任编辑:陈书欣

甘肃省自然科学基金资助项目（3ZS061-A25-058）；甘肃省高校研究生导师科研计划项目（0811-05）

姬五胜（1968-），男，甘肃秦安人，教授，博士，主要从事微波电路三维集成、计算微波等方面的研究。