非负矩阵谱半径的估计

李 华，杨静梅

（1.河南城建学院数理系，河南平顶山 467044；2.河北科技大学理学院，河北石家庄 050018）

非负矩阵谱半径的估计

李 华1，杨静梅2

（1.河南城建学院数理系，河南平顶山 467044；2.河北科技大学理学院，河北石家庄 050018）

借助2个新的矩阵，利用Frobenius G不等式，得出一种易于计算的新的估计方法，得出非负矩阵谱半径的上下界，最后通过实例说明该方法的优越性。

非负矩阵；谱半径；估计

1 问题的提出

非负矩阵在计算数学、图论、自动控制等领域有着广泛的应用，对其特征值尤其是谱半径的估计在矩阵理论中有重要的意义。如果上下界能表示为易于计算的函数，那么这种估计的价值更高。用A≥0（aij≥0）来表示A是非负矩阵，记ρ（A）为n阶非负矩阵A的谱半径。设A＝（aij）是n阶非负矩阵，称

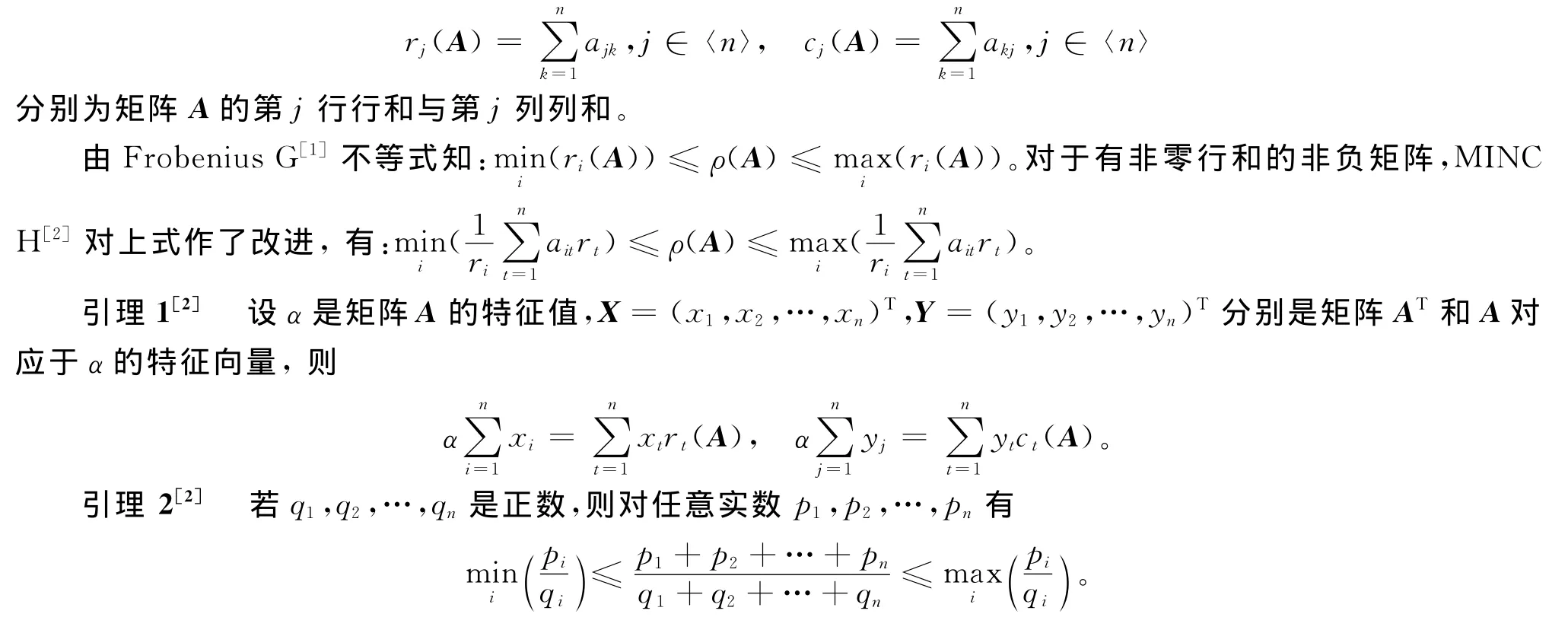
2 主要结果

3 数值例子

表1 比较结果Tab.1 Comparsion of the results

实际上，ρ（A）＝5.741 657 38，由此可知，定理1得到的结果在一定程度上要优于以往的结果。

［1］ FROBENIUS G.Uber Matrizen aus nicht Negativen Elementen［M］.Berlin：S B Press，1912.

［2］ MINC H.Nonnegative Matrices［M］.Wew York：Wiley，1988.

［3］ LIU Shu-lin.Bounds for the greatest characteristic root of a nonnegative matrix［J］.Lin Alg Appl，1996，239：151-160.

［4］ 殷剑宏.非负矩阵最大特征值的新界值［J］.数值计算与计算机应用（Journal on Numerical Methods and Computer Applications），2002，23（4）：282-295.

［5］ 刘明丽，黄廷祝，刘小琴.非负矩阵最大特征值的新界值［J］.电子科技大学学报（Journal of University of Electronic Science and Technology of China），2007，36（2）：343-345.

［6］ 李 莉，霍丽君，李志梅.辛几何上具有仲裁的认证码的一类新构作［J］.河北科技大学学报（Journal of Hebei University of Science and Technology），2010，31（4）：294-299.

Estimation of perron root of nonnegative matrices

LI Hua1，YANG Jing-mei2
（1.Department of Mathematics and Physics，Henan University of Urban Construction，Pingdingshan Henan 467044，China；2.College of Sciences，Hebei University of Science and Technology，Shijiazhuang Hebei 050018，China）

In this paper，a new simple-calculating estimation method based on two new matrices are obtained by using the Frobenius inequality.Therefore a convergence sequence of lower bounds and upper bounds of the perron root can be constructed.Some examples are given to show the effectiveness of the new method is effective.

nonnegative matrices；perron root；estimateion

O151.21

A

1008-1542（2011）04-0313-03

2010-09-10；责任编辑:张 军

李 华（1978-），女，河南南阳人，讲师，硕士，主要从事数值代数与矩阵谱估计方面的研究。