21～30阶群嵌入置换群的一些讨论①

徐峰

(运河高等师范学校，山西运城 221300)

21～30阶群嵌入置换群的一些讨论①

徐峰②

(运河高等师范学校，山西运城 221300)

本文主要讨论了21阶到30阶的群到置换群的最小嵌入，并讨论了最小嵌入的个数及共轭类划分，并且最终得到了所有的结果.

低阶群;最小嵌入;置换群;共轭类

0 引言

在文献［4］中，作者根据凯莱定理：一个群都同构于一个变换群，讨论了1到20阶群到置换群的最小嵌入，并得到了所要的结果。从而想到：对于更高阶的群，是不是也存在到置换群的最小嵌入?方法是否相同?这些嵌入是否唯一?本文就接下去讨论21到30阶的情况。

文中，ρ－1aρ的运算顺序是从右向左.G＜H表示G是H的子群;Sn表示n次对称群;m(G)= min{n∈NG＜Sn};［a，b］=a－1b－1ab，即G中元素a，b的换位子;Zn表示模n剩余类加群，它是个n阶循环群;如果S是群G的子集，记〈S〉为G中由S所生成的子群。

1 交换群到置换群的嵌入

首先，我们先对交换群G来确定m(G)的值.我们有如下定理：

定理一(有限交换群结构定理)有限交换群G可以分解为一些阶等于素数幂的循环群的直积，且这样的分解方法是唯一的(定理及证明均见参考文献［4］)。

定理三m( Zpn)=pn，其中p为素数(定理及证明均见参考文献［4］)。

接下来，我们将对所有从21阶到30阶的交换群进行讨论：

1.1 21阶交换群

故由定理二，m(G21，1)≤3+7=10，若G21，1可以嵌到Sn中，则Sn中存在21阶元b，若b为21阶轮换，则n≥21，若b为不相交轮换的乘积，则这些轮换阶数的最小公倍数为21，则一定存在一个3阶和7阶的不相交的轮换，故n≥10。综上知m(G21，1)=10。

1.2 22阶交换群

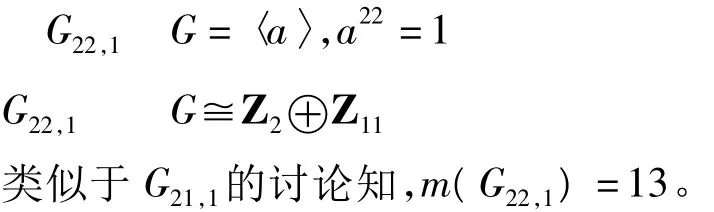
1.3 23阶交换群

1.4 24阶交换群

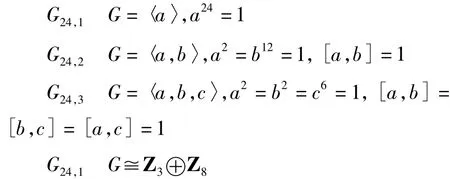
类似于G21，1的讨论知，m(G24，1)=11。

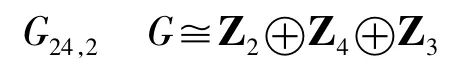
根据定理二，m(G24，2)≤2+4+3=9，考虑到G8，2＜G24，2，m(G8，2)=6，故m(G24，2)≥6，但S6中不含12阶元，故m(G(24，2))不能为6.若m(G24，2)=7，则12阶元只能为不相交的3阶和4阶轮换的积，如b=(123)(4567)，则与b可交换的2阶元只能为b6，矛盾，故m(G24，2)≠7。若m(G24，2)=8，则12阶元为不相交的3阶和4阶轮换的积，类似于上面讨论，也不可能，所以m(G24，2)=9。

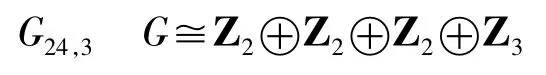
根据定理二，m(G24，2)≤9.由于G8，3＜G24，3，m(G8，3)=6，若m(G24，3)=6，则6阶元只能形如c=(123456)，或不相交的2阶、3阶轮换之积，比如c=(12)(345)。当c=(123456)时，与之可交换的2阶元仅有c3，矛盾。当c=(12)(345)时，与之可交换的2阶元仅有(12)=c3，矛盾.故m (G24，3)≠6.若m(G24，3)=7，则6阶元只能形如c=(123456)或c=(12)(345)或c=(12)(34) (567)。对于c=(123456)，与之可交换的2阶元仅有b3，矛盾。对于c=(12)(345)，与之交换的2阶元仅有c3=(12)、(67)、(12)(67)，但可验证，由(12)、(67)、(12)(67)中的任两个与(12) (345)三者生成群的阶＜24，故也不可能。对于c=(12)(34)(567)，与之交换的2阶元仅有(12)、(34)、(12)(34)、(13)(24)、(14)(23)，也可以验证，由(12)(34)(567)与(12)、(34)、(12) (34)、(13)(24)，(14)(23)中的任两个可交换的元生成的群的阶＜24，也不可能。故m(G24，3)≠7.若m(G24，3)=8，则6阶元形如c=(123456)或(12)(345)或(12)(34)(567)或(12)(345) (678)。若c=(123456)则与之交换的2阶元仅有c3和(78)以及c3(78)，矛盾。若c=(12) (345)则与之交换的2阶元有c3=(12)、(67)、(78)、(68)以及(12)(67)、(12)(78)、(12) (68)。也可验证，由c=(12)(345)与上面任两个可交换的2阶元所生成的群的阶＜24，矛盾.若c=(12)(345)(678)则与之可交换的2阶元仅有c3=(12)、(36)(47)(58)、(37)(48)(56) (38)(46)(57)、(12)(36)(47)(58)、(12)(37) (48)(56)、(12)(38)(46)(57)，但由c与上述任两个可交换的2阶元生成的群的阶小于24。故m(G24，3)≠8.综上知m(G24，3)=9。

1.5 25阶交换群

1.6 26阶交换群

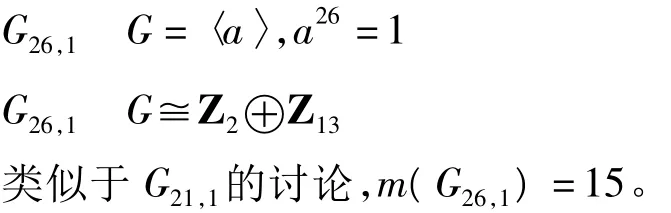
1.7 27阶交换群

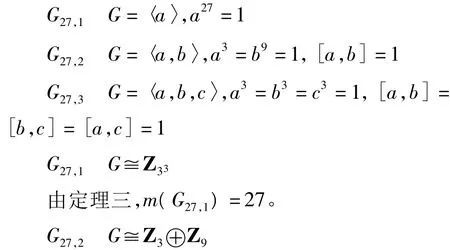
由定理二，m(G27，2)≤12。设G27，2可嵌入Sn中，则27|n!，故n≥9。当9≤n＜12时，9阶元只能形如b=(123456789)，此时除b3，b6之外无3阶元与b可交换，故n=12，即m(G27，2)=12。

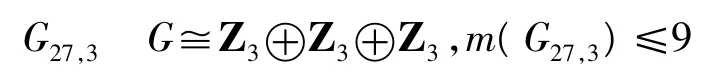
从G27，2中的讨论可看出m(G27，3)=9。

1.8 28阶交换群

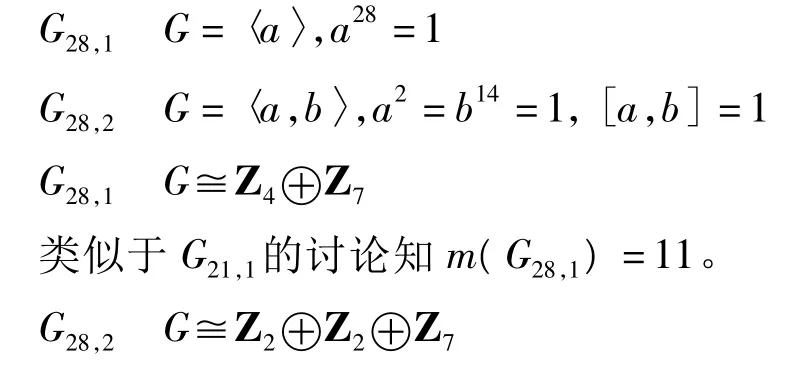
由定理二，m(G28，2)≤2+2+7=11.考虑到G14，1＜G28，2，m(G14，1)=9，故m(G28，2)只能为9或10或11.若m(G28，2)=9或10，则14阶元只能是不相交的2阶、7阶轮换的乘积，不妨设为b= (12)(3456789)，则要想有除b7=(12)之外的2阶元与b交换，m(G28，2)至少为11，且这个元为(10 11)或(12)(10 11)，故m(G28，2)=11。

1.9 29阶交换群

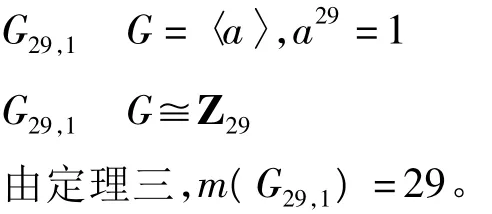
1.10 30阶交换群

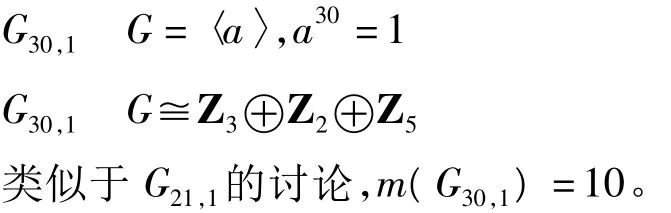
这样，就得到了在交换的情况下，21～30阶群嵌入置换群的最小嵌入。

1.11 关于低级交换群嵌入置换群的猜测总结

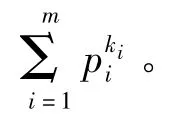
2 非交换群到置换群的嵌入

关于一些特殊的非交换群，我们也有一些已有结论：

定理四如果p为奇数，Dp可以嵌到Sp中，

(定理及证明均见参考文献［4］)。

定理五如果p为奇数，设n=2p，则Dn可以嵌到Sm中，其中m=p+2，

(定理及证明均见参考文献［4］)。

基于定理四、定理五和一些分析，我们来讨论非交换群的情况：

2.1 21阶非交换群

G21，2G21，2中含有7阶元，故m(G21，2)≥7.此时取a=(1234567)，b=(253)(467)，不难验证，a、b生成的群与G21，2同构，故m(G21，2)=7。

2.2 22阶非交换群

2.3 24阶非交换群

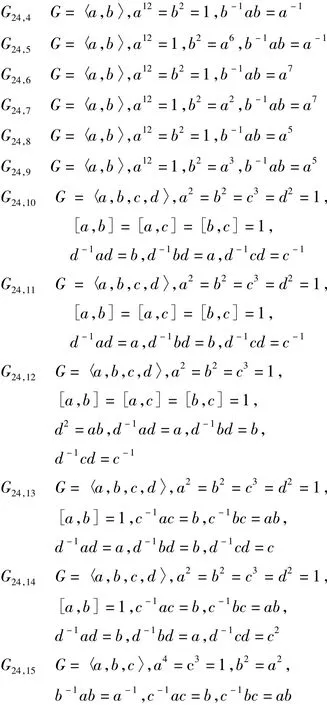
G24，4G24，4含有12阶元，故m(G24，4)≥7，若令a=(1234)(567)，b=(24)(67)不难验证这两个元生成的群与G24，4同构，故m(G24，4)=7。

G24，5G24，5含有12阶元，故m(G24，5)≥7，若m(G24，5)≤10，则a=(1234)(567)或与一个不相交的2阶轮换的乘积或与一个不相交的3阶轮换的乘积，但不管怎样a6等于(13)(24)，则对应4阶生成元b满足b2=(13)(24)，b中含有一个4阶轮换(1234)或(1432)，但不管怎样，都不满足b－1ab=a－1，故12阶元a至少含两个不相交的4阶轮换。若令a=(1234)(5678)(9 10 11)，b= (1638)(2547)(10 11)，不难验证这两个生成的群与G24，5同构，故m(G24，5)=11。

G24，6G24，6含有12阶元，故m(G24，6)≥7，若令a=(1234)(567)，b=(24)，不难验证，这两个元生成的群与G24，6同构，故m(G24，6)=7。

G24，7G24，7含有12阶元，故m(G24，7)≥7，设m(G24，7)≤10，则12阶生成元a只能为(1234) (567)或再乘上一个2阶轮换，或再乘上一个3阶轮换。但不管怎样a2含有(13)(24)，让a2=b2，则b包含一个4阶轮换(1234)或(1432)，但不管怎样，b－1ab≠a7(a7∶1→4，b－1ab∶1→2)。故a至少含两个4阶轮换.若令a=(1234)(5678)(9 10 11)，b=(1638)(2547)(9 10 11)，不难验证，这两个元生成的群与G24，7同构，故m(G24，7)=11。

G24，8G24，8含有12阶元，故m(G24，8)≥7，若令a=(1234)(567)，b=(67)，不难验证，这两个元生成的群与G24，8同构，故m(G24，8)=7。

G24，9b为8阶元，故b至少含一个8阶轮换，从b2=a3可以看出，a至少含两个4阶轮换，从而m(G24，9)≥11.若令a=(1432)(5876)(9 10 11)，b=(15263748)(10 11)，不难验证，这两个元生成的群与G24，9同构，故m(G24，9)=11。

G24，10由a，b，c三个元生成的群Gabc为G24，10的子群，且Gabc≅Z2⊕Z2⊕Z3，由前面交换群嵌入的讨论可知，m(Gabc)=7，则m(G24，10)≥7.若令a=(12)(34)，b=(14)(23)，c=(567)，d=(67) (13)，不难验证，这四个元生成的群与G24，10同构，故m(G24，10)=7。

G24，11类似于G24，10的讨论，m(G24，11)≥7.若令a=(12)，b=(34)，c=(567)，d=(67)，不难验证，这三个元生成的群与G24，11同构，故m (G24，11)=7。

G24，12类似于G24，10的讨论，m(G24，12)≥7.从d2=ab看出，d至少含有一个4阶轮换。若d仅含有一个4阶置换，不妨设d=(1234)，则d2=ab =(13)(24)，此时a=(13)，b=(24)，或a= (12)(34)，b=(14)(23)或a=(14)(23)，b= (12)(34)，或分别乘上一些除1，2，3，4之外的不相交的2阶轮换，但不管怎样，a与d都不可交换。故d至少含有两个4阶轮换，则m(G24，12)≥8。若m(G24，12)=8，则b只能为(1234)(5678) b2=(13)(24)(57)(68)，满足d2=ab，d－1ad= a，d－1bd=b的可交换的二阶元a、b只能为a= (13)(24)，b=(57)(68)或a=(13)(57)，b= (24)(68)或a=(13)(68)，b=(24)(57)(忽略a和b的对称性)，此时找不到与a、b、d都可交换的三阶元d，故m(G24，12)≠8，类似地可讨论知m (G24，12)≠9，10。若令a=(12)(34)，b=(56) (78)，c=(9 10 11)，d=(1324)(5768)(10 11)不难验证它们生成的群与G24，12同构，故m (G24，12)=11。

G24，13由a，b，c这三个元生成的群与G12，5同构，而m(G12，5)=4，故m(G24，13)≥4.若m (G24，13)=4或5，则不存在与3阶元c可交换的2阶元d。若令a=(14)(23)，b=(13)(24)，c= (234)，d=(56)，不难验证，这三个元生成的群与G24，13同构，故m(G24，13)=6。

G24，14类似于G24，13的讨论，m(G24，14)≥4.若令a=(14)(23)，b=(13)(24)，c=(234)，d= (34)，不难验证，这三个元生成的群与G24，14同构故m(G24，14)=4。

G24，15G24，15含有4阶元，故m(G24，15)≥4.若m(G14，15)≤7，则4阶生成元a为一个4阶轮换或再乘上一个2阶轮换。不妨假设a含有(1234)则a2=(13)(24)，由b2=a2知，b含有(1432)或含有(1234)。不管怎样，b－1ab≠a－1，故a至少含有2个4阶轮换，即m(G24，15)≥8.若令a= (1234)(5678)，b=(1836)(2745)，c=(258) (476)，不难验证，这三个元生成的群与G24，15同构，故m(G24，15)=8。

2.4 26阶非交换群

G26，2G=〈a，b〉，a13=b2=1，b－1ab=a－1

G26，2G26，2≅D13，故m(G26，2)≤13，又G26，2中含13阶元，故m(G26，2)≥13。故m(G26，2) =13。

2.5 27阶非交换群

G27，4G27，4中含有9阶元，故m(G27，4)≥9，若令a=(123456789)，b=(285)(369)，不难验证，这两个元生成的群与G27，4同构，故m(G27，4)=9。

G27，5由a，b生成的群与G9，2同构，而m(G9，2) =6，故m(G27，5)≥6，若m(G27，5)=6，则3阶生成元a可由一个3阶轮换或两个3阶轮换相乘生成。若a=(123)，则与之可交换的3阶元为(132)，(456)，(465)或它们与一个不相交的3阶轮换的乘积。但此时不管b、c怎么选取都不能使c－1bc=ba.若a=(123)(456)，则与之可交换的3阶元为(132)、(465)、(123)、(456)或它们中含有1的3轮换与含4的3轮换的乘积，但不管怎么选取b、c，都不能使c－1bc=ba，从而m(G27，5)≠6.同样可讨论m(G27，5)≠7，8.若令a=(123) (456)(789)，b=(148)(259)(367)，c=(147) (258)(369)，不难验证，这3个元生成的群与G27，5同构，故m(G27，5)=9。

2.6 28阶非交换群

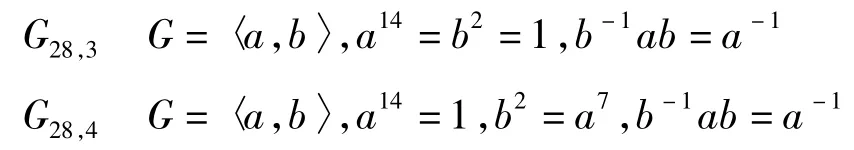
G28，3G28，3≅D14，由定理五，m(G28，3)≤9，又G28，3中含14阶元，故m(G28，3)≥9，故m(G28，3)=9。

G28，4G28，4中含14阶元，故m(G28，4)≥9.若m (G28，4)=9，则a=(12)(3456789)，a7=(12)，满足b2=a7=(12)的b不存在。类似讨论m (G28，4)≠10。若令a=(12)(34)(567891011)，b =(1324)(6 11)(7 10)(89)，不难验证这两个元生成的群与G28，4同构，故m(G28，4)=11。

2.7 30阶非交换群

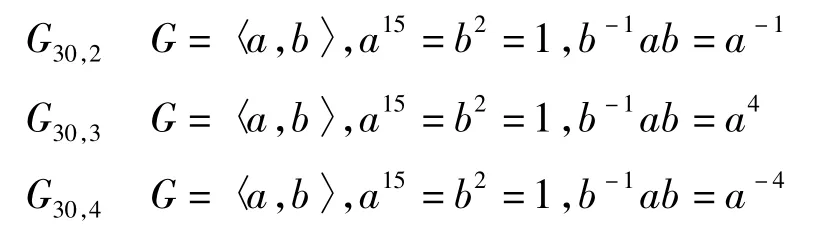
G30，2G30，2中含15阶元，故m(G30，2)≥8。若令a=(123)(45678)，b=(23)(58)(67)，不难验证这两个元生成的群与G30，2同构，故m(G30，2)=8

G30，3G30，2含有15阶元，故m(G30，3)≥8若令a=(123)(45678)，b=(58)(67)，不难验证这两个元生成的群与G30，3同构，故m(G30，3)=8。

G30，4G30，4含有15阶元，故m(G30，4)≥8若令a=(123)(45678)，b=(23)，不难验证这两个元生成的群与G30，4同构，故m(G30，4)=8。

3 最小嵌入个数、共轭类的讨论

前面完成了21～30阶群到置换群的最小嵌入的讨论，但这些嵌入是不是唯一的?如果不唯一，到底有多少种不同的最小嵌入?它们之间有什么关系?

先来看看Klein四元群K={e，a，b，ab}，它可嵌入S4，但K≅G1={(1)，(12)，(34)，(12) (34)}，K≅G2={(1)，(24)，(13)，(13)(24)} K≅G3={(1)，(14)，(23)，(14)(23)}，K又同构于G4={(1)，(12)(34)，(13)(24)，(14) (23)}。显然，G1≅G2≅G3是互相共轭的，而与G4共轭的只有G4。

由上述两种，可见，有必要讨论21～30阶群到置换群的最小嵌入的个数，共轭分类。

(P55，定理12)文献［1］告诉我们：n次对称群中两置换为共轭的充要条件是它们为同型的置换.设π、τ为二同型置换，写为循环表示时应有：

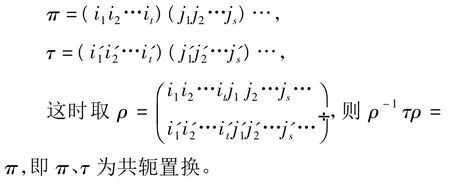
先证明下述定理：

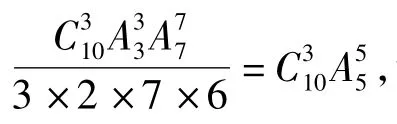
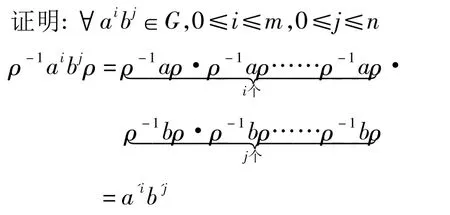
由此可见，ρ－1Gρ⊆G'，同理可证ρ－1Gρ⊇G'，所以ρ－1Gρ=G'。

事实上，此时G，G'在H的内自同构意义下是同构的(H的内自同构σρ在其上的限制作用)。

从而可见，讨论最小嵌入的共轭问题。只需要看它们的生成元是否共轭，也即它们的生成元是否是同型的。而对于决定共轭的元素“ρ”，用上面给出的方法可以具体求出来，但考虑到最小嵌入的个数之巨大，下面的讨论就不具体写出来。

先看交换情况下，21～30阶群到置换群嵌入个数、共轭类的讨论。

G21，1m(G21，1)=10.21阶元只能由3阶元和7阶元的乘积生成，则它的最小嵌入的个数为它们为同型的，根据文献［1］定理12(P55)，它们为同一个共轭类。

最小生成元为一个，最小生成元集为{a= (123)(45678910)}。

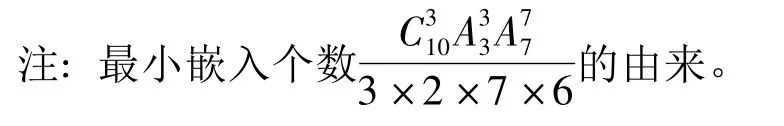
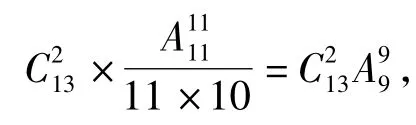
最小生成元为一个，最小生成元集为{a= (12)(345)(6 7 8 9 10)}。

至此交换情况下最小嵌入个数、共轭类的讨论完毕。

关于非交换的情况可分为两类讨论(对于嵌入S6的除外，因为S6有外自同构)。第一类：不存在可交换的生成元，如G21，1，G22，2，G24，4，G24，5等等。这种情况下，在共轭的意义下，它们的嵌入都是唯一的，也即只有一个共轭类。而关于最小嵌入个数的讨论，用排列组合的知识很容易得到。第二类：存在一些可交换的生成元，如G24，10，G24，11，G24，12，等等。这种情况下，交换的部分可用前面交换群嵌入置换群的方法进行讨论，再结合第一类的讨论可以得到最小嵌入个数、共轭类的讨论。

分别各举一例说明上述的两类情况，比如G22，2和G24，10。

这样，21～30阶群到置换群的最小嵌入个数、共轭类的讨论完毕。

到此，我们得到了所要的结果。

［1］张远达.有限群构造(上，下)［M］.北京，科学出版社，1982

［2］韩士安，林磊.近世代数［M］.北京，科学出版社，2004

［3］http：//wims.math.ecnu.edu.cn/华东师范大学数学系网上对谈式数学服务器(WIMS) Group模块

［4］张通.关于低阶群嵌入置换群的一些讨论［D］.华东师范大学数学系，2005

［5］苑金枝，曹洪平.23p阶群的一个新刻画［J］.西南大学学报，2008

On the embedding from groups with order 21～30 into symmetric groups

XU Feng

(Higher Normal School of Canal，Yuncheng Shanxi221300)

In this paper，we discuss minimal embeddings from groups with order 21～30 into symmetric groups.Moreover，the number of minimal embeddings and the number of conjugate classes are given.

group with lower order;minimal embedding;symmetric group;conjugate class

O211.6

A

1672－7169(2011)03－0064－08

2011－05－23

徐峰(1972－)，女，江苏新沂人，硕士，运河高等师范学校数学与科学系教师。