Nielsen系统的特殊统一对称性和特殊守恒量

王肖肖，张美玲，贾利群，田燕宁

(江南大学理学院，江苏无锡 214122)

Nielsen系统的特殊统一对称性和特殊守恒量

王肖肖，张美玲，贾利群，田燕宁

(江南大学理学院，江苏无锡 214122)

研究时间不变的群的特殊无限小变换下Nielsen系统的特殊统一对称性，研究由特殊统一对称性导致的特殊守恒量——特殊Noether守恒量、特殊Hojman守恒量和特殊Mei守恒量.

特殊无限小变换;Nielsen系统;特殊统一对称性;特殊守恒量

0 引言

约束力学的对称性和守恒量理论是现代分析力学领域的一个研究热点［1－10］.Noether对称性通过Noether等式可以找到Noether守恒量;时间不变的特殊Lie对称可以找到Hojman守恒量;Mei对称性一般可以找到Mei守恒量.而统一对称性则可以一次性找到Noether守恒量、Hojman守恒量和Mei守恒量.

统一对称性理论是梅凤翔等人在2004年提出的.此后，统一对称性理论被发展到准坐标下的一般完整约束系统、有多余坐标的完整系统、非完整约束力学系统、Hamilton力学系统、一些复杂的力学系统和Birkhoff系统.应用领域还涉及Vacco动力学系统和机电系统［11］.文献［12］研究了完整系统Nielsen方程的统一对称性与守恒量.

然而，在这些统一对称性和守恒量理论中，除了Hojman守恒量外，都是在时间变化的群的无限小变换下的对称性和守恒量理论.本文将在时间不变的群的特殊无限小变换下，研究Nielsen系统的特殊统一对称性以及由特殊统一对称性导致的特殊Noether守恒量、特殊Hojman守恒量和特殊Mei守恒量.

1 Nielsen系统的运动微方程

引进时间不变的群的特殊无限小变换

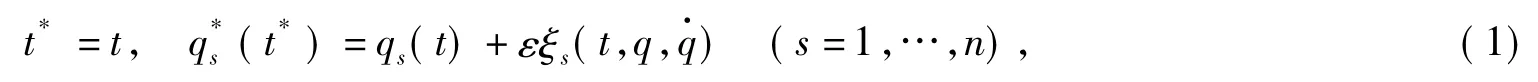
其中ε为无限小参数，ξs为无限小生成元.变换(1)的无限小生成元向量以及无限小生成元向量的一次扩展和二次扩展分别为

2 Nielsen系统的特殊对称性导致的特殊守恒量

特殊的Noether对称性是Hamilton作用量在特殊的无限小变换(1)下的一种不变性.

命题1如果存在规范函数GN=GN(t，q，)使无限小生成元ξs满足如下特殊Noether等式

那么，这种不变性称为Nielsen系统的特殊Noether对称性，特殊Noether对称性导致如下的特殊Noether守恒量

证明(9)式两端对时间t求导，利用特殊Noether等式(8)和方程(6)可得=0，即命题1成立.

特殊的Lie对称性是微分方程在时间t不变的群的特殊无限小变换(1)下的一种不变性.由定义可知，Nielsen系统方程(6)的特殊Lie对称性的确定方程为

命题2如果Nielsen系统方程(6)在特殊无限小变换(1)下的生成元ξs满足特殊Lie对称性的确定方程(10)，且存在某函数μ=μ(t，q，)，使得

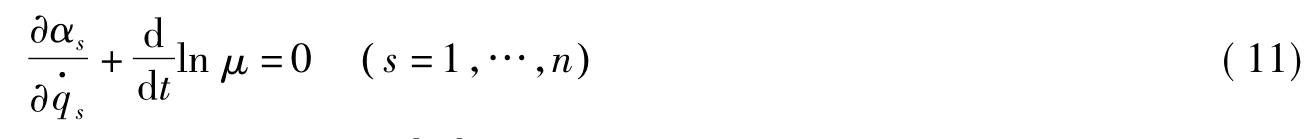
成立，则系统的特殊Lie对称性将导致特殊Hojman守恒量［13］

特殊的Mei对称性是用经特殊无限小变换(1)变换后的动力学函数代替变换前的动力学函数而使Nielsen系统方程(6)的形式保持不变的一种对称性.由定义可得Nielsen系统方程(6)的特殊Mei对称性的判据方程为

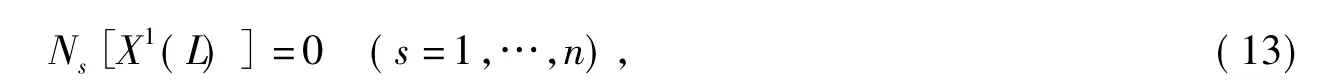
命题3如果Nielsen系统方程(6)在特殊无限小变换(1)下的生成元ξs满足方程(13)，且存在规范函数GM=GM(t，q，)满足如下结构方程

则Nielsen系统方程(6)的特殊Mei对称性导致的特殊Mei守恒量为

证明(15)式两端对时间t求导，利用特殊Mei对称性的判据方程(13)和结构方程(14)可证明= 0，即命题3成立.

3 Nielsen系统的特殊统一对称性及其导出的特殊守恒量

定义如果Nielsen系统方程(6)的对称性同时为特殊Noether对称性、特殊Lie对称性和特殊Mei对称性，这样的对称性称为Nielsen系统方程(6)的特殊统一对称性.

判据对于Nielsen系统方程(6)如果存在，满足如下方程

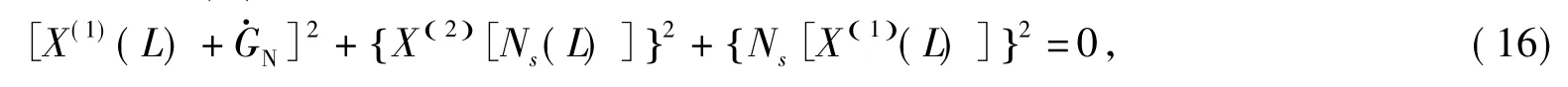
则相应的对称性为Nielsen系统方程(6)的特殊统一对称性.

命题4对于Nielsen系统方程(6)，特殊的统一对称性可导致形如(9)式的特殊Noether守恒量.

命题5对于Nielsen系统方程(6)，如果存在某函数μ=μ(t，q)满足(11)式，则特殊的统一对称性可导致形如(12)式的特殊Hojman守恒量.

命题6对于Nielsen系统方程(6)，如果存在规范函数GM=GM(t，q，)满足结构方程(14)，则特殊的统一对称性可导致形如(15)式的特殊Mei守恒量.

4 结论

本文给出了Nielsen系统的特殊统一对称性的定义和判据，给出了Nielsen系统的特殊统一对称性直接导致的特殊Noether守恒量的形式、Hojman守恒量的形式、特殊Mei守恒量的形式.本文的结果可进一步推广到Nielsen体系的其他领域.

［1］MEI F X，WU H B.Form invariance and new conserved quantity of generalized Birkhoffian system［J］.Chin Phys B，2010，19(5):050301(1－4).

［2］SHANG M，MEI F X.Poisson theory of generalized Birkhoff equations［J］.Chin Phys B，2009，18(8):3155－3157

［3］WU H B，MEI F X.Symmetry of Lagrangians of nonholonomic systems of non-Chetaev’s type［J］.Chin Phys B，2010，19(3):030303(1－4).

［4］CUI J C，ZHANG Y Y，YANG X F，et al.Mei symmetry and Mei conserved quantity of Appell equations for a variable mass holonomic system［J］.Chin Phys B，2010，19(3):030304(1－5).

［5］LI Y M，MEI F X.Stability for manifolds of equilibrium states of generalized Birkhoff system［J］.Chin Phys B，2010，19(8):080302(1－3).

［6］ZHANG Y.Poisson theory and integration method of Birkhorffian systems in the event space［J］.Chin Phys B，2010，19(8):080301(1－5).

［7］XIA L L，CAI J L.Conformal invariance and conserved quantities of a general holonomic system with variable mass［J］.Chin Phys B，2010，19 (4):040302(1－6).

［8］许学军，梅凤翔.准坐标下一般完整系统的统一性［J］.物理学报，2005，54(12):5521－5524.

［9］JIA L Q，XIE Y L，ZHANG Y Y，et al.A type of new conserved quantity deduced from Mei symmetry for Appell equations in a holonomic system with unilateral constraints［J］.Chin Phys B，2010，19(11):110301(1－5).

［10］贾利群，解银丽，罗绍凯.相对运动动力学系统Appell方程Mei对称性导致的Mei守恒量［J］.物理学报，2011，60(4):040201(1－4).

［11］罗绍凯，张永发.约束系统动力学研究进展［M］.北京:科学出版社，2008.

［12］李元成，王小明，夏丽莉.完整系统Nielsen方程的统一对称性与守恒量［J］.物理学报，2010，59(5):2935－2938

［13］梅凤翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.

Special Unified Symmetry and Special Conserved Quantity of Nielsen System

WANG Xiao-xiao，ZHANG Mei-ling，JIA Li-qun，TIAN Yan-ning

(School of Science，Jiangnan University，Wuxi 214122，China)

Under special infinitesimal transformations of groups in which the time is invariable，special unified symmetry of Nielsen system and special Noether conserved quantity，special Hojman conserved quantity and special Mei conserved quantity deduced from special unified symmetry are investigated.

special infinitesimal transformations;Nielsen system;special unified symmetry;special conserved quantity

O316

A

1007－0834(2011)03－0022－03

10.3969/j.issn.1007－0834.2011.03.008

2011－03－28

中央高校基本科研业务费专项资金(JUSRP31102)资助

王肖肖(1987—)，女，吉林四平人，江南大学理学院在读硕士研究生，研究方向:应用数学、一般力学.