Nielsen系统Mei对称性的新型守恒量

张美玲，王肖肖，贾利群，田燕宁

(江南大学理学院，江苏无锡 214122)

Nielsen系统Mei对称性的新型守恒量

张美玲，王肖肖，贾利群，田燕宁

(江南大学理学院，江苏无锡 214122)

研究Nielsen系统Mei对称性的新型守恒量.在群的无限小变换下，由Nielsen系统Mei对称性的定义和判据，得到Nielsen系统Mei对称性的一种新结构方程和一种新型守恒量.

Nielsen系统;Mei对称性;结构方程;新型守恒量

0 引言

2000年，梅凤翔首次提出了一种新的对称性［1］，Mei对称性:经过无限小变换后，约束力学系统中的动力学函数仍满足原方程的对称性.2000年到2007年间，国内众多学者在Mei对称性方面的研究成果在文献［2］和文献［3］中得到了很好的反映.此后，Mei对称性依然是分析力学界研究的热点［4－16］.方建会对Lagrange系统Mei对称性直接导致的一种新的守恒量［17］进行了研究.本文将研究Nielsen系统Mei对称性的一种新结构方程和一种新型守恒量.

1 Nielsen系统的Mei对称性和Mei对称性的判据［2］

设Nielsen系统的位形由广义坐标qs(s=1，2，…，n)确定，且受到理想双面完整约束，其Lagrange函数L和动力学方程分别为

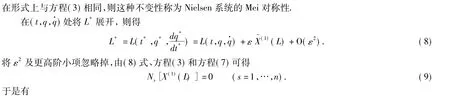
判据如果时间和广义坐标的无限小变换(4)中的ξ0和ξs满足方程(9)，则Nielsen系统(2)相应的不变性即为该系统的Mei对称性，方程(9)即为该系统Mei对称性的判据方程.

2 Nielsen系统Mei对称性的一种新结构方程和一种新型守恒量

命题如果Nielsen系统(2)的Mei对称性的生成元ξ0，ξs以及规范函数GX=GX(t，q，q·)满足如下新型结构方程

显然，方程(10)是Nielsen系统Mei对称性的一种新的结构方程，方程(11)式是与Mei对称性相应的一种新的守恒量.

3 结论

本文给出了Nielsen系统Mei对称性的一种新的结构方程和一种新的守恒量.本文的结果是对约束力学系统Mei对称性与Mei守恒量理论的发展和提高，该结果可在单面约束以及非完整约束力学系统领域进行推广和应用.

［1］MEI F X.Form invariance of Lagrange system［J］.J Beijing Inst Technol，2000(2):120－124.

［2］梅凤翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.

［3］罗绍凯，张永发.约束系统动力学研究进展［M］.北京:科学出版社，2008.

［4］JIA L Q，XIE J F，ZHENG S W.Structure equation and Mei conserved quantity for Mei symmetry of Appell equation［J］.Chin Phys B，2008，17 (1):17－22.

［5］DING N，FANG J H.Perturbation to Mei symmetry and adiabatic invariants for Hamilton systems［J］.Chin Phys B，2008，17(5):1550－1553.

［6］JIA L Q，XIE J F，LUO S K.Mei symmetry and Mei conserved quantity of nonholonomic systems with unilateral Chetaev type in Nielsen style［J］.Chin Phys B，2008，17(5):1560－1564.

［7］ZHANG M J，FANG J H，ZHANG X N，et al.Perturbation to Mei symmetry and Mei adiabatic invariants for mechanical systems in phase space［J］.Chin Phys B，2008，17(6):1957－1961.

［8］FANG J H，LIU Y K，ZHANG X N.New conserved quantities of Noether-Mei symmetry of mechanical system in phase space［J］.Chin Phys B，2008，17(6):1962－1966.

［9］贾利群，解银丽，罗绍凯.相对运动动力学系统Appell方程Mei对称性导致的Mei守恒量［J］.物理学报，2011，60(4):040201(1－4).

［10］葛伟宽.一类完整系统的Mei对称性与守恒量［J］.物理学报，2008，57(11):6714－6717.

［11］蔡建乐.一般完整系Mei对称性的共形不变性与守恒量［J］.物理学报，2009，58(1):22－27.

［12］WANG P，FANG J H，WANG X M.A generalized Mei conserved quantity and Mei symmetry of Birkhoff system［J］.Chin Phys B，2009，18(4): 1312－1315.

［13］CUI J C，ZHANG Y Y，JIA L Q.Mei conserved quantity of Nielsen equation for anon-Chetaev-type non-holonomic system［J］.Chin Phys B，2009，18(5):1731－1736.

［14］崔金超，贾利群，杨新芳.Chetaev型非完整系统Appell方程Mei对称性的结构方程和Mei守恒量［J］.河南师范大学学报:自然科学版，2009，37(2):70－73.

［15］CUI J C，ZHANG Y Y，YANG X F，et al.Mei symmetry and Mei conserved quantity of Appell equations for a variable mass holonomic system［J］.Chin Phys B，2010，19(3):030304(1－5).

［16］PANG T，FANG J H，ZHANG M J，et al.A new type of conserved quantity deduced from Mei symmetry of nonholonomic systems in terms of quasi-coordinates［J］.Chin Phys B，2009，18(8):3150－3154.

［17］方建会.Lagrange系统Mei对称性直接导致的一种守恒量［J］.物理学报，2009，58(6):3617－3619.

A New Type of Conserved Quantity Deduced from Mei Symmetry for a Nielsen System

ZHANG Mei-ling，WANG Xiao-xiao，JIA Li-qun，TIAN Yan-ning
(School of Science，Jiangnan University，Wuxi 214122，China)

A new type of conserved quantity deduced from Mei symmetry of a Nielsen system is studied.Under the infinitesimal transformation of groups，a new structural equation is established and a new conserved quantity deduced from Mei symmetry of a Nielsen system is obtained from the definition and the criterion of Mei symmetry of a Nielsen system.

Nielsen system;Mei symmetry;structure equation;a new type of conserved quantity

O316

A

1007－0834(2011)03－0019－03

10.3969/j.issn.1007－0834.2011.03.007

2011－03－28

中央高校基本科研业务费专项资金(JUSRP31102)资助

张美玲(1986—)，女，黑龙江齐齐哈尔人，江南大学理学院在读硕士研究生，研究方向:应用数学、一般力学.