利用Origin拟合方法处理牛顿环实验数据
2011-12-25王晓雄
王晓雄
(南京理工大学,江苏南京 210094)
利用Origin拟合方法处理牛顿环实验数据
王晓雄
(南京理工大学,江苏南京 210094)
探讨如何利用图像识别和Origin拟合功能处理牛顿环实验结果的方法。
Origin软件;牛顿环;数据处理;拟合
从推导牛顿环干涉条纹的光强分布公式入手,介绍借助图像识别获得牛顿环光强分布并利用Origin进行拟合获得平凸透镜曲率半径的方法。通过牛顿环光强分布规律的介绍可以使学生更好地了解光的干涉现象,并且借助于Origin的拟合技术可以减小实验误差。
1 实验原理
牛顿环仪的光路如图1所示。平行光垂直入射到平凸透镜平面。平凸透镜的曲率半径为 R,球心为O。下面我们推导半径为 r处的干涉圆环的光强公式。当光入射到 A点时,部分光反射,部分光透射。透射光在B点反射后与A点反射的光发生干涉。A点和B点反射的两束光的光程差为:
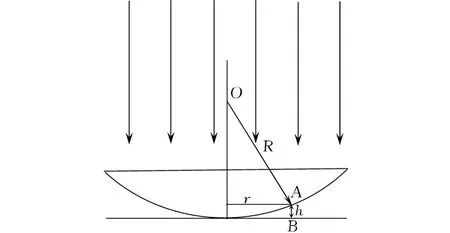
图1 牛顿环仪的光路示意图
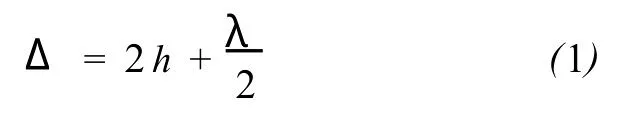

我们假设 A点反射的平面波方程为Ψ1=Aei(kr+φ0),其中φ0为初相位,B点反射光在A处的波动方程为 Ψ2=A′ei(kr+φ0+δΦ)。两束光干涉后的波动方程为Ψ=Ψ1+Ψ2。干涉光的光强分布为:
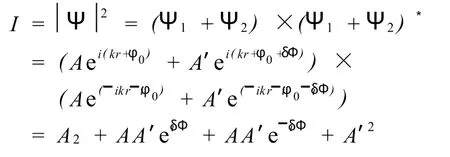
为简单起见,假设两路反射光的振幅相等,即A=A′。由此可得牛顿环的光强分布公式简化为 :I=A2+2AA2cosδ φ +A2,为了简化问题 ,同时又能保持处理方法的一致性,我们令A=1。则最终的光强分布公式为:
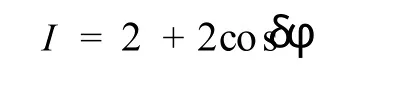
2 实验结果和数据处理
利用上式可以计算出牛顿环的光强分布。我们根据实验中使用的参数,即 R=855mm,入射光波长λ=589.3nm,计算了光强 I随牛顿环半径r的变化情况,结果见图2。
从图2可以看出,中心位置由于半波损失在平凸透镜凸面与平晶紧密接触的情况下是半径较大的暗圆,再次证明了我们在测量牛顿环的半径时不通过确定圆心测半径,而通过测量直径来测得凸面曲率半径的必要性。而且,随着半径的增加,相邻暗纹之间的间隔越来越小,锐度变得越来越大,从而有助于我们能比较好地通过肉眼来判断暗纹的中心位置,所以在试验中是测量干涉级次为4~13的各暗条纹的位置,这样可以有效的减小由于暗纹中心位置确定不准所导致的误差。
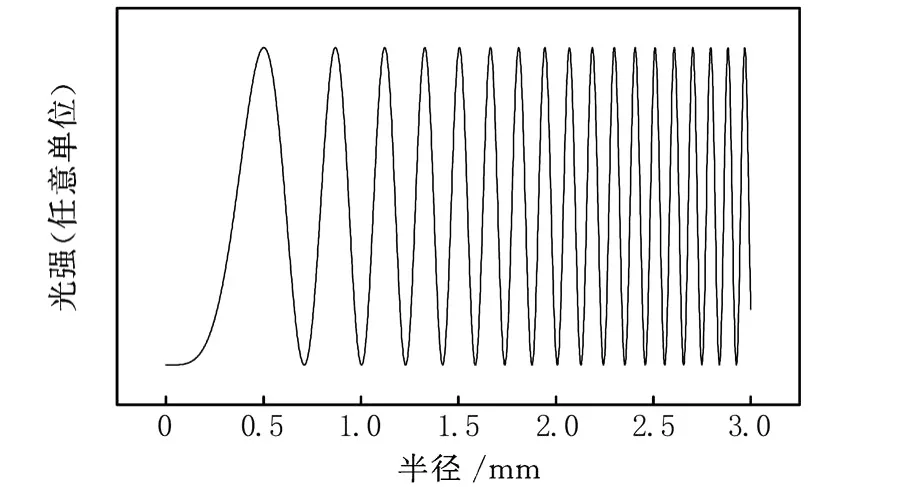
图2 牛顿环沿半径方向的光强分布变化
上面是根据已知的实验参数来获得牛顿环的光强分布,下面我们介绍如何通过获得某一直线上光强的分布通过Origin的拟合功能来获得待测的参数R。为了使我们能集中于数据处理的理论方法,而避开过多的图像处理的技巧,利用前面推导的光强分布函数计算了沿某一弦方向L的光强分布,计算参数为λ=589.3nm,XX=0.5mm,YY=5mm,R=855mm,如图3右图中实线所示。为了使方法具有较广的适用性我们并没有假设获取的光强分布是沿半径方向的。将光强分布随半径的变化情况输入Origin中,然后利用Origin的非线性拟合的高级拟合工具通过自定义拟合函数来拟合数据。输入的拟合函数定义式为:y=y=2+2*cos(((2*(R-sqrt(R^2-(x-XX)^2-YY^2))+lamda/2)*2*PI)/lamda),其中R为平凸透镜的曲率半径,XX为x轴的偏移,YY为y轴方向的偏移,lamda为入射光的波长,固定在589.3nm。经拟合后得到了各个拟合参数的值,曲率半径R=854.80 mm,YY为5.05mm,XX为0.50 mm,与计算所使用的参数相差无几,这充分表明了这种处理方法的优势。但是,在拟合过程中也发现,这种方法对于拟合参数的初始值依赖性比较大,如果提供的初始拟合参数偏离标准值较大则可能会导致发散,最终不能获得需要的参数。其次,原始的光强分布是通过理论计算获得的,可以说是非常理想的。但是在实际实验中如果是通过CCD摄像头摄像后提取的,就不可避免的存在噪音、非线性扭曲等等问题,而这些因素都会给最后的拟合带来负面影响。
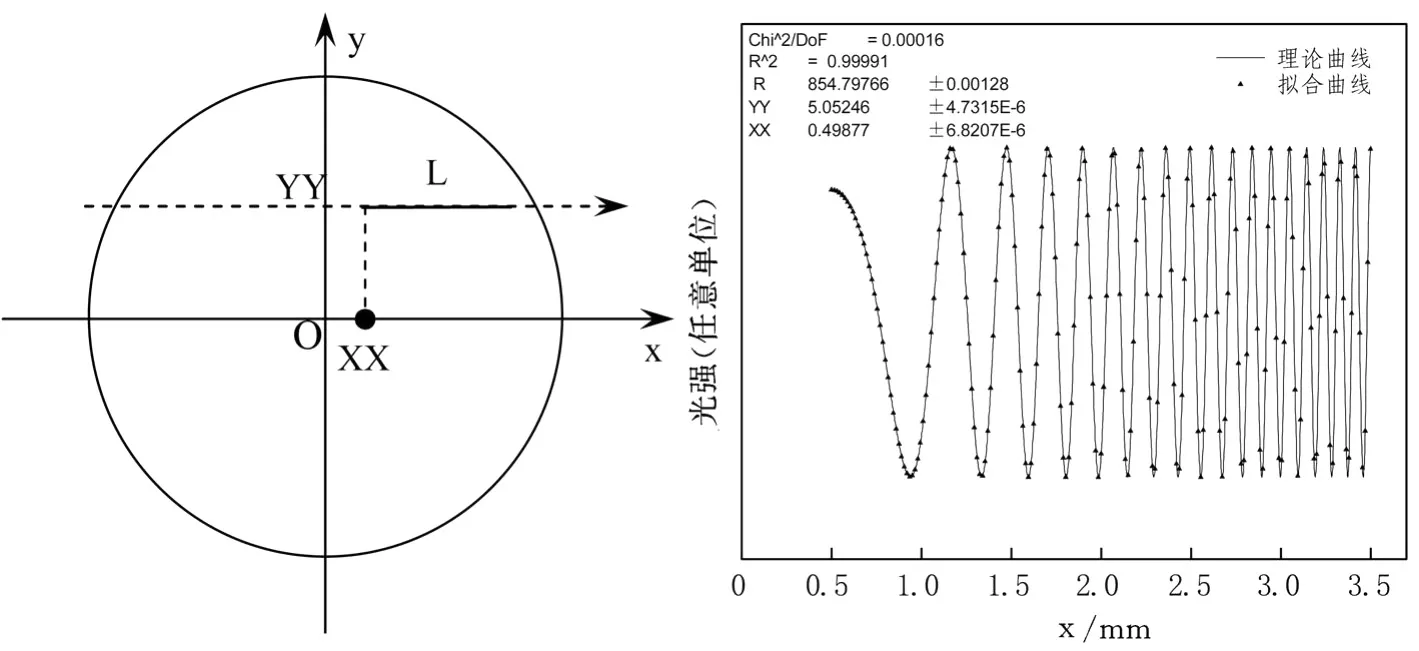
图3 某弦线L上光强分布的示意图
3 结 论
通过理论分析,计算了牛顿环试验中光强的理论分布,并以此为基础,介绍了如何利用简单的图像识别结合Origin的自定义函数拟合来处理牛顿环实验数据的方法。这种方法简单易行,而且可以让学生更深入地了解牛顿环实验。
[1]李相银.大学物理实验[M].北京:高等教育出版社,2009.
[2]周剑平.精通Origin 7.0[M].北京:北京航空航天大学出版社,2005.
[3]刘绒侠,王党社,彭首军.用origin软件处理物理实验数据[J].大学物理实验,2008(3):30-32.
Processing the Experimental Data of Newton Circle with Origin Fitting
WANG Xiao-xiong
(Nanjing University of Science&Technology,Nanjing 210094)
In this article we demonstrate the method of processing the experimental data of Newton Circle with image identification and origin fitting.
origin program;Newton circle;data processing;fitting
O4-33
A
1007-2934(2011)04-0073-02
2011-02-26
南京理工大学高等教育学会资助
