高拱坝开裂危险性分析

张 冲，王仁坤，赵文光，尤 林，赵 艳

(中国水电顾问集团成都勘测设计研究院，四川 成都 610072)

1 前 言

根据国际大坝委员会1988年所作关于大坝工作状态的调查报告[1]，在失事的243座混凝土坝中，有30座是由裂缝问题引起的，同时大量正常运行的混凝土大坝，也均不同程度出现开裂问题。研究表明，拱坝中存在裂缝，不仅仅使得拱坝外观变差，大坝的整体性、连续性遭受破坏，还使得大坝的稳定性和防渗性减弱，裂缝中的静水压力会使得拱坝向下游的位移增加，从而减弱拱坝中梁的作用；裂缝漏水更是使得混凝土内的钙离子析出和流失，严重的会导致坝体漏水，缩短拱坝寿命，甚至影响大坝的安全。因此裂缝已经成为混凝土坝病变的主要反映之一，会破坏大坝的整体性，降低大坝的强度，影响大坝的稳定，危及混凝土坝的安全运行。随着破损与失事大坝数量的增多，人们日益关注大坝的安全性，探求大坝的破损机理，完善大坝的设计准则。

近40年以来，随着有限元等数值分析技术的发展、物理模型试验技术的进步，拱坝开裂仿真分析取得了巨大的进步，尤其是断裂力学的提出，使得研究拱坝开裂机理、判断危害程度及预测后续发展成为可能，如1976年Hillerborg提出虚拟裂缝模型，以应变软化机理将非线性本构关系引入混凝土材料的断裂分析。Carpinteri、Feltrin等学者将其应用于混凝土坝的开裂研究。在Hillerborg的研究基础上，Bazant于1983年提出的钝断裂带理论，广泛应用于混凝土坝的裂缝模拟。Vargas-Loli和Fenves较早研究了混凝土的受拉开裂行为对重力坝在地震荷载作用下的非线性响应的影响；Bhattacharjee和Leger较为系统地研究了重力坝在静、动力荷载下的非线性响应规律。Ghaemian和Ghobarah、Tinawi、Espandar和Lotfi、王少敏、张楚汉和周元德等人也对此进行了研究，取得了丰富成果[1]。目前的各类方法均从结构应力与变形的角度出发，考虑材料的破坏和屈服，但不考虑材料不同受力状态导致的混凝土强度差异。这些方法均比较复杂，属于前瞻性研究阶段，实用性较低。

真实的拱坝在运行过程中，坝身混凝土的受力多处于复杂应力状态之下。试验研究揭示，当混凝土处于多轴拉压状态，混凝土的抗压强度将达不到单轴抗压强度，抗拉强度也达不到单轴抗拉强度。这种情况下如采用混凝土单轴强度准则来设计双轴拉压状态的混凝土结构将是偏于不安全的。而当混凝土处于多轴受压状态，混凝土的抗压强度将高于单轴抗压强度，此时如采用混凝土单轴强度设计，就会使整个结构的设计偏于保守，浪费材料。考虑到混凝土强度的多轴效应，因此目前很多国家如日本、俄罗斯、英国、美国等的设计规范[2]均引入了混凝土的双轴强度准则。我国开展混凝土多轴强度准则研究也势在必行。但由于试验的困难，目前国内外混凝土试件多轴强度的结果较少，其中绝大部分均为湿筛小试件双轴压压以及拉压状态下的试验结果，三轴试验结果尤其是全级配混凝土大试件的三轴试验结果尚不多见。此外，双轴情况下的拉拉组合以及三轴情况下的拉拉拉组合的试验结果离散性太大，尚不能为科研和工程所用。

本文将充分吸收国内外各类混凝土试件的试验结果，并对其进行整理和综合分析，综合考虑湿筛小试件和全级配大体积混凝土的关系，考虑各种应力组合状态对混凝土屈服和破坏的影响，提出了高拱坝开裂危险性分析的查图算法。该算法立足大量实验数据，简单实用，容易为普通工程设计人员所掌握。

2 混凝土受力状态及破坏行为

2.1 双向应力状态

对于一个湿筛立方体小试件，一个方向应力为σ1，另一个方向应力为σ2，第三面自由，应力以拉应力为正，压应力为负，综合各类试验结果，其在双向应力作用下大体表现出如下几种破坏形态[2]：

(1)劈裂(如图1(a)所示)。混凝土试件处于双向受压状态下，且α=σ1/σ2较大，在0.75～1.0之间，由于试件在双向均受到较大的压缩变形，因而只能在垂直于自由面的方向产生拉应变，根据应力比的不同，形成大致平行于自由面的裂缝。破坏时往往伴随有爆炸似的声响。

(2)斜向压剪破坏(如图1(b)所示)。试件处于双向受压状态下，应力比α较小，在0.25～0.5之间，破坏时，平行于自由面方向与平行于压应力较大方向的裂缝都比较发育，但最终主裂缝一般出现在与自由面成10°～20°角的方向。当试件处于拉压受力状态下，且拉应力小于1/15压应力时，也可能出现类似破坏现象。

(3)斜向拉剪破坏(如图1(c)所示)。当试件处于拉压状态，且拉应力相对较大时，裂缝往往垂直于自由面，同时与最大压应力方向成45°角左右的方向发展。与斜向压剪破坏不同的是，这种情况下，裂缝较为集中，损伤从主裂缝处向两侧迅速衰减。

(4)正向拉裂(如图1(d)所示)。当试件处于双向受拉状态，且一方拉应力远小于另一方向拉应力时，破坏时裂缝往往只有一条，且裂缝方向垂直于最大拉应力方向，试件其余部分损伤不大。

(5)斜向拉裂(如图1(e)所示)。当试件处于双向受拉状态，且双向拉应力大致相等时，裂缝与主应力方向基本成45°角开裂。裂缝往往只有一条，损伤从主裂缝方向向两侧迅速衰减。

图1 双轴应力状态下混凝土的破坏形态

图2是根据试验成果整理的应力空间双轴强度包络图[4-9]。由图可见，混凝土在双轴压状态下的抗压强度比单轴压状态下的大，其强度变化与应力比呈明显的相关性。其一般规律为：当应力比α=0.0～0.2时，混凝土试件强度增长较快；当应力比α=0.2～0.6时，强度变化趋于平稳，混凝土试件的最高抗压强度一般发生在这个阶段，例如当α=0.5时，大部分试件的强度比单轴抗压强度提高25%以上；当应力比α=0.7～1.0时，其抗压强度增长值开始降低，如当应力比α=1.0，也就是双向等压时，混凝土试件强度比单轴抗压强度仅提高了16%。

混凝土试件在双轴拉压状态下，其抗压强度、抗拉强度均比单轴抗压和抗拉强度有所降低。大量的试验表明，在这种状态下，其混凝土抗压、抗拉强度随压应力比重的增加呈现凹线型降低的现象(如图3所示)。但在实际分析中，为了计算方便，通常采用近似直线来模拟，如图2所示。

混凝土试件在双轴拉状态下，国内外试验结果的离散性均较大，在各种不同应力比状态下，有的试验结果抗拉强度比单轴抗拉强度增加，有的大致相等，有的降低，目前对此还没有统一的认识。考虑到该区域并不是水工结构力学研究的重点，为了简单起见，本文近似认为，在双轴拉状态下，不管应力比多大，其双轴抗拉强度均等于单轴抗拉强度。

图2 双轴应力状态下混凝土的破坏包络线

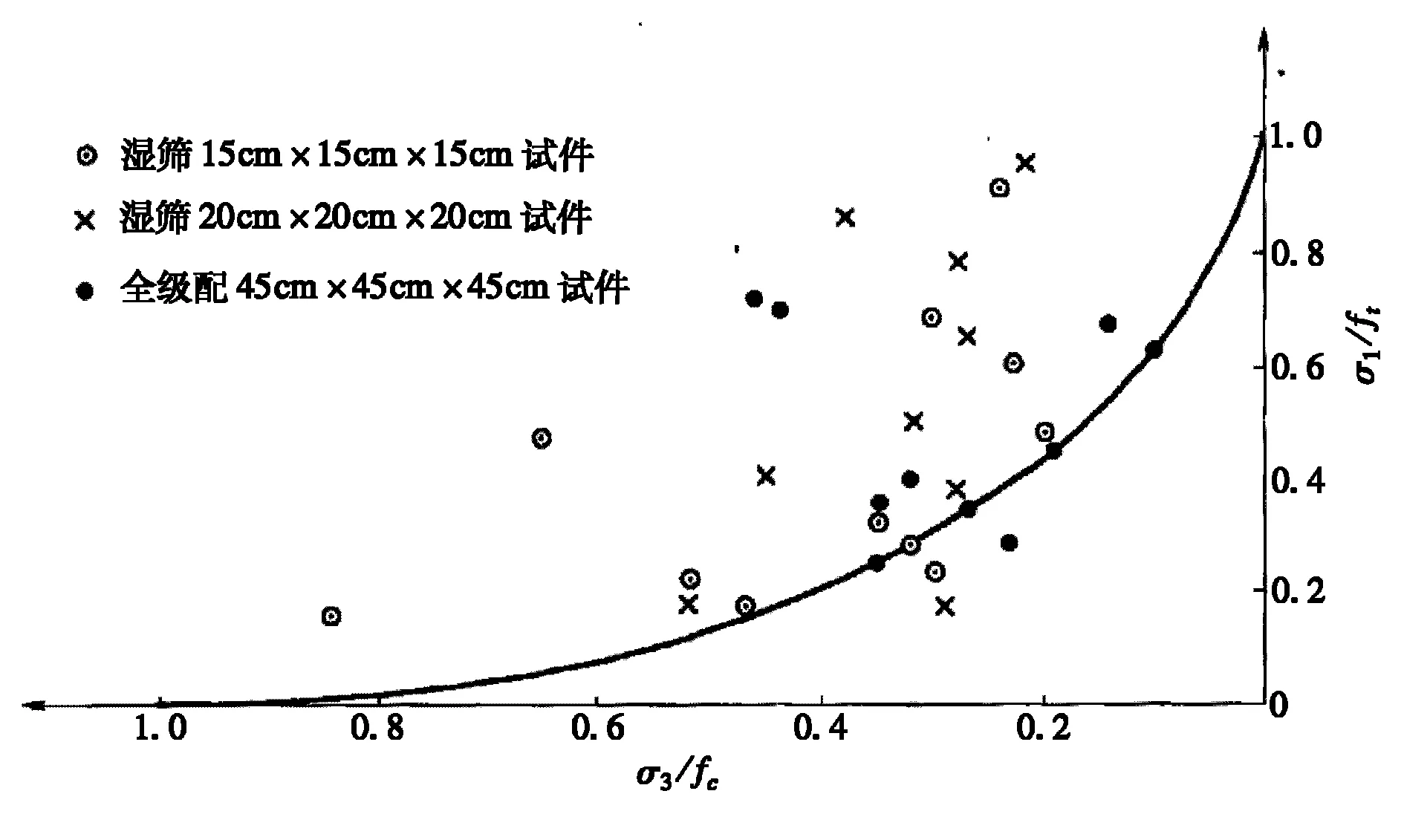
图3 双向应力状态破坏点强度包络

图4给出了相应的拉压状态应力-应变关系曲线，从图中可以看出，在双轴拉压状态下，混凝土的抗压强度随着拉应力的增加迅速降低，当拉应力约为压应力10%时，混凝土试件抗压强度只有相应的单轴抗压强度的60%左右；进一步，当拉应力增加到压应力的20%左右，强度则降低为单轴抗压强度的40%。对拱坝而言，0%～20%之间的拉压应力比是一种常见的工作状态，尤其是在靠近坝肩的部位，因此，以往以单轴强度设计校核的拱坝在这种应力状态下是偏于不安全的。

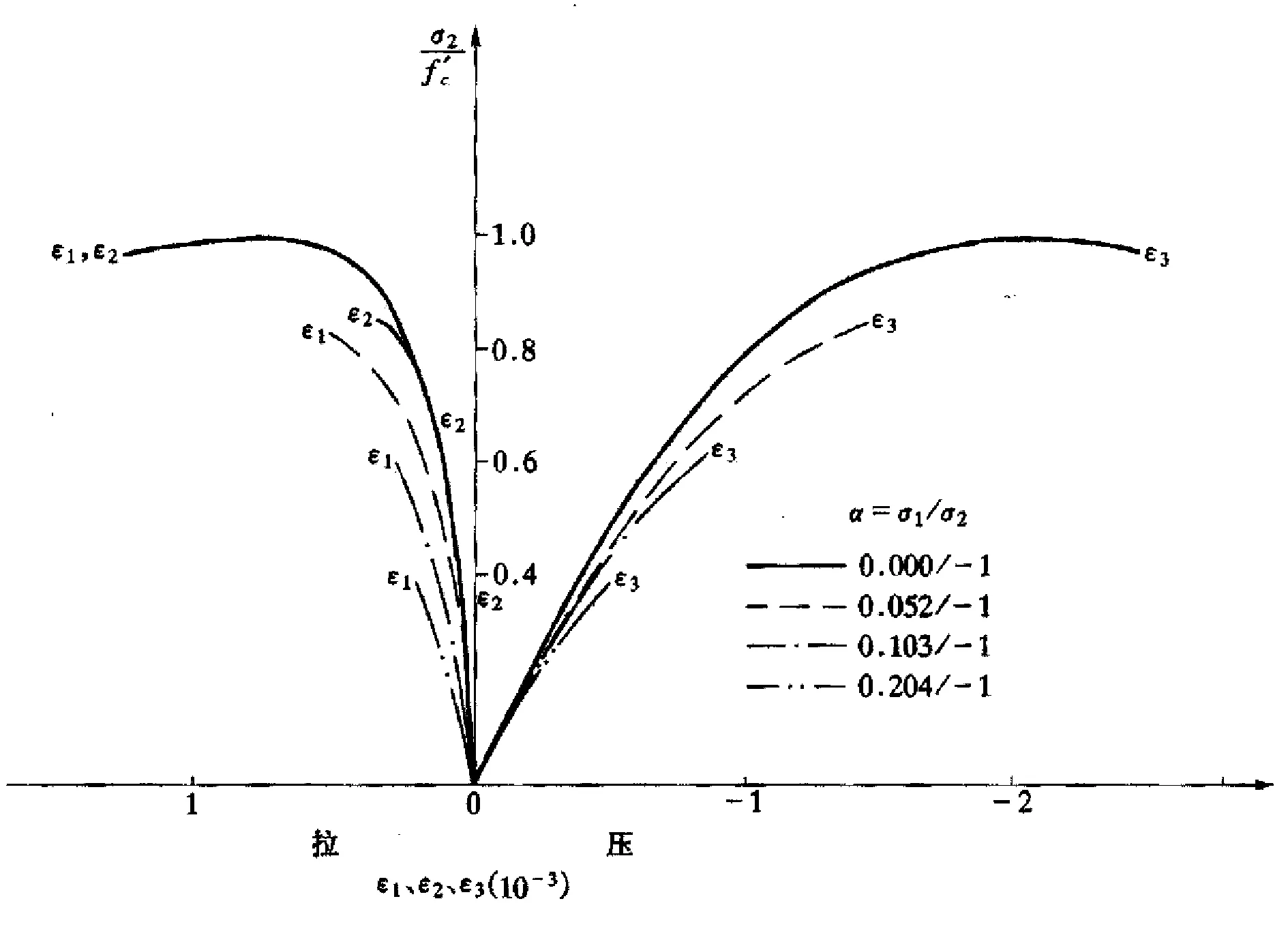
图4 双轴拉压状态下混凝土的应力-应变关系曲线

2.2 三向应力状态

三向受力状态下，混凝土立方体试件的开裂破坏过程取决于三轴应力状态下的拉压组合状态以及各向应力的比值，大体可以归纳为以下五种典型的破坏形态[2]：

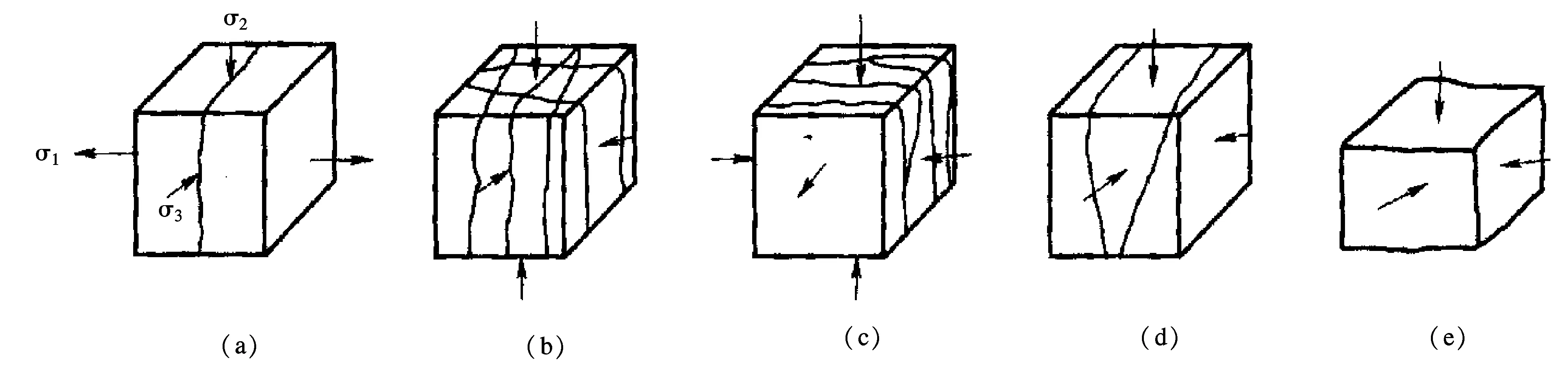
图5 三向应力状态下混凝土的破坏形态

(1)拉断破坏(如图5(a)所示)。试件一般沿垂直于最大主拉应力方向发生突然断裂，裂缝通常只有一条，界面清晰，近似为一个平面，裂缝两旁的混凝土几乎没有损伤。绝大多数试件裂缝平行于试件表面，但对于两拉一压试验，当应力比α=0.3～1.0时，裂缝可能与最大主应力σ1成某一夹角或者发生分叉裂缝，无一定的规律性。一般情况下，三轴拉压(α=|σ1/σ3|≥0.1)以及三轴拉状态容易发生这类破坏形式。

(2)柱状压坏(如图5(b)所示)。这种破坏主要见于三轴压状态α1=|σ1/σ3|、α2=|σ2/σ3|均比较小的情况，如α1≤0.1，α2≤0.1。此时，在主压应力σ3作用下，两个非主压向由于泊松效应逐渐变成拉应变。当两侧向的拉应变超过混凝土的极限拉应变，就形成平行于σ3的裂缝，并逐渐延伸，以至贯通全试件，构成分离的短柱群而最终压坏。破坏时，试件内混凝土已经普遍受到损伤。

(3)层状劈裂破坏(如图5(c)所示)。在三轴拉压状态，当拉应力σ1所占比例很小不能形成垂直于σ1方向的拉断破坏，而α2=|σ2/σ3|又较大，则破坏时将形成片状劈裂破坏。另外，在三轴受压状态，当α1=|σ1/σ3|很小而α2=|σ2/σ3|较大时，足以阻止沿垂直于σ2轴方向发生劈裂时，试件同样会沿着σ2σ3平面形成层状劈裂破坏。层状劈裂破坏的试件，一般有若干个主要的劈裂面，破坏面的界面不是非常清晰，两旁的混凝土损伤较大。因为混凝土的非匀质性、粗骨料的形状和分布都是随机的，宏观的平行劈裂面有不规则的倾斜角。

(4)斜剪破坏(如图5(d)所示)。在三轴受压状态，当α1=|σ1/σ3|相对较大，足以阻止试件发生层状劈裂破坏，同时α2=|σ2/σ3|也足够大，以至可以限制试件发生柱状压坏，则试件呈斜剪破坏。发生该种破坏时，在垂直于σ2方向的试件表面形成二条宏观斜裂缝，与主压应力σ3方向成20°～30°夹角。

(5)挤压流动(如图5(e)所示)。这种破坏只发生在三向等压或α1=|σ1/σ3|、α2=|σ2/σ3|都较大的状态。这种状态下，混凝土试件的三个主应力方向都发生压应变，试件不会出现拉裂缝。对于三向非等压情况，破坏时主压应力方向发生很大的压缩变形。由于较大的σ1、σ2的作用形成了强有力的侧向约束，试件内部材料在三向压力下发生塑性流动，试件形状由立方体变成长方体，此时试件内部构造受到很大破坏，粗骨料和砂浆都已有明显的相对错位，一些质地软弱的粗骨料甚至被压碎。卸载后，可发现裂缝及个别骨料压裂、压酥的现象，且体积减小。

将双轴应力状态作为三轴应力状态的一种特殊状态，综合各类破坏实验[2-9]，利用八面体正应力、剪应力坐标进行划分，可以大体划分成如图6所示的破坏区域[10]。

图6 三向应力状态下混凝土破坏区域划分

2.3 全级配混凝土多轴应力状态

成都院与大连理工大学联合进行的高强度大体积混凝土材料特性研究显示[11]，全级配大体积混凝土在多轴受力状态下，一般有如下规律：

(1)无论是全级配试件还是湿筛试件，无论是大试件还是小试件，双轴拉压状态下的混凝土抗拉、抗压强度均低于相应的单轴抗拉、抗压强度，所以应力强度比均小于1.0。

(2)在同一拉压应力比之下，对于全级配大混凝土试件和湿筛二级配大混凝土试件，虽然尺寸均为45cm×45cm×120cm，但湿筛二级配大混凝土试件的强度普遍高于全级配大混凝土试件相应应力比的强度，如应力比σ1/σ2=-0.05时，湿筛试件的抗压强度平均值为8.68MPa，而全级配试件抗压强度的平均值为7.03MPa。

(3)对于湿筛试件，即湿筛二级配大小试件之比，小尺寸试件的强度高于相应应力比的大尺寸试件的强度，如15cm×15cm×30cm的湿筛小试件在应力比为σ1/σ2=0.05时的抗压强度为10.30MPa，而相应的湿筛大尺寸试件45cm×45cm×120cm的抗压强度为8.68MPa。

从破坏形态上看，大试件(湿筛、非湿筛)在双轴拉压状态下，试件裂缝与拉应力方向基本垂直，属于典型的拉断型破坏。图7给出了不同试件在同一应力比0.2∶-1情况下典型的裂缝曲线，从中可以看出，裂缝的分布规律大体相似，且均只有一条主裂缝，主裂缝周围混凝土损伤较小。这与小试件的开裂行为是有显著差异的。

图7 全级配混凝土大试件破坏时裂缝展开

从以上各种实验可以看出，混凝土在多轴受力状态下的破坏特性和破坏形态要远远比在单轴受力状态下的破坏特性和破坏形态复杂的多，且各种不同的破坏形态和破坏特性往往取决于混凝土三向应力比的大小，对于一固定范围的应力比，其破坏形态大致相似。

3 拱坝开裂危险性之查图算法[12]

3.1 三轴压缩状态

根据大量混凝土实验数据 ，在三轴压状态下：

(1)混凝土的σ3/fc要比单轴压状态提高很多，如试件的压应力比为1∶0.1∶0.1时，其三轴抗压强度是单轴强度的2倍多，且随着应力比σ1/σ3的增大，三轴抗压强度σ3/fc成倍增加(见表1)。

表1 混凝土三轴抗压试验强度汇总

(2)第二主应力σ2对三轴抗压强度有一定的影响，影响的大小一方面由σ1/σ3决定，即σ1/σ3越大，影响越大；另一方面，也由σ2/σ3决定，一般而言，强度会随着中间主应力的提高呈现先提高后降低的现象，最大值一般出现在σ2/σ3=0.3～0.6之间，但中间主应力的影响不会超过25%。

(3)低标号混凝土的三轴抗压强度比高标号混凝土的三轴抗压强度增幅明显，且σ1/σ3越小，增加效应越显著。将各类混凝土实验数据绘制在σ3/fc～σ2/σ3图中，其规律如图8所示。

考虑到在三轴压状态下，中间主应力对强度影响不大，为了更加方便地利用混凝土试验结果，对图8作了充分的简化(见图9)。首先是忽略了中间主应力的影响；其次采用适当保守的原则，推荐设计强度按实验低值进行统计。注意该算法及公式只适用于σ1/σ3在0.0～0.35之间的情况，不可做任意的外延，外延部分目前尚没有可靠的试验数据支持。

(1)

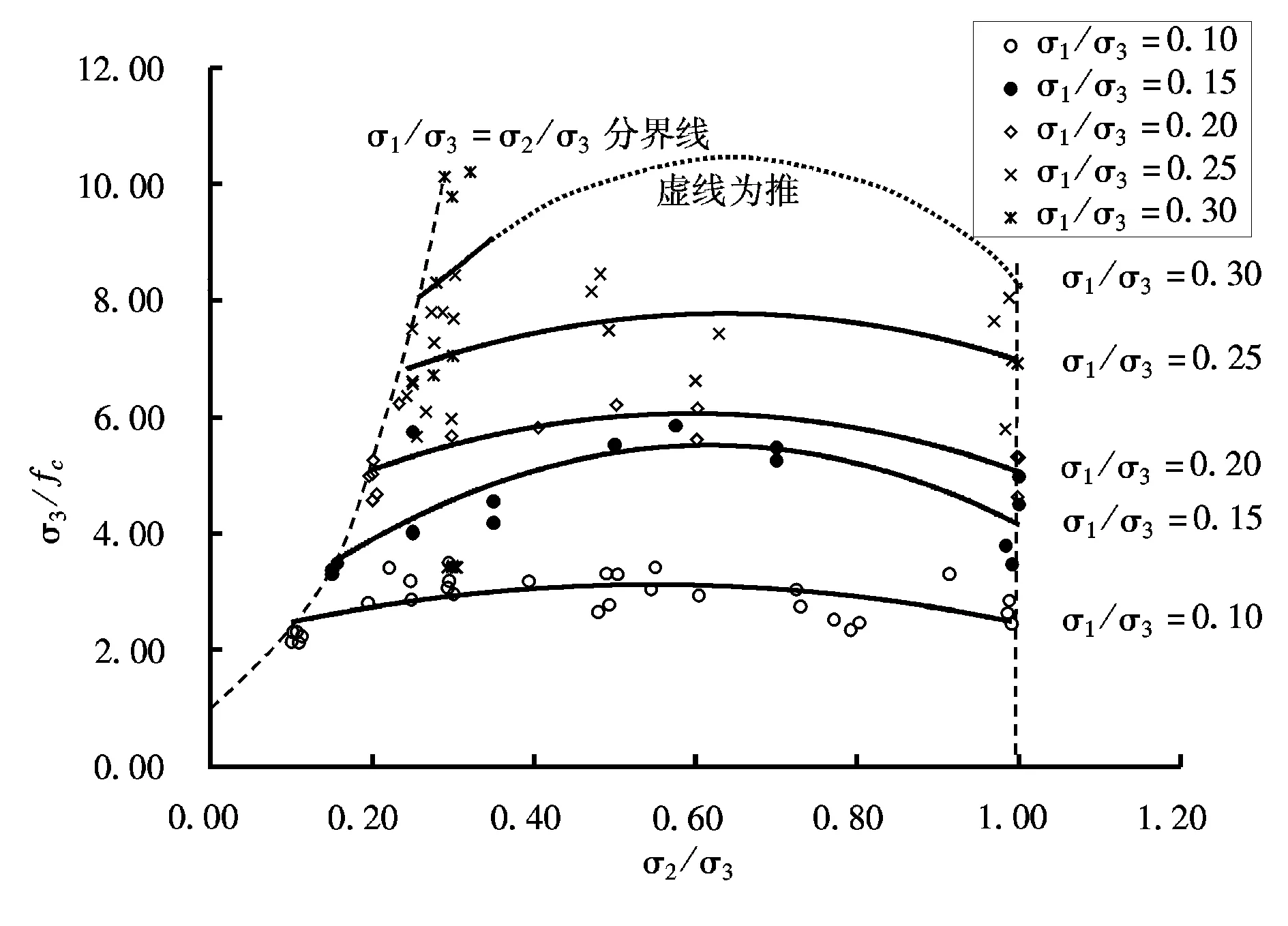
图8 三轴压缩情况下混凝土抗压强度曲线

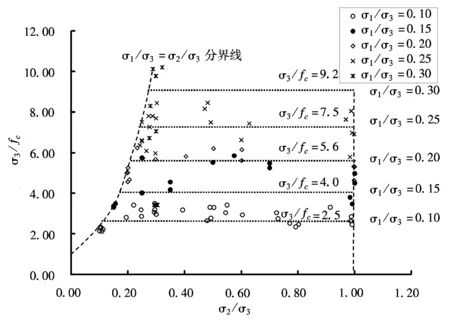
图9 三轴压缩情况下混凝土试验简化成果曲线

3.2 三轴拉压组合状态

在三轴拉压状态下，随着侧向小主拉应力σ1的加大(拉应力加大，σ1/σ3减小)，三轴混凝土抗压强度迅速降低，且均显著低于混凝土的单轴抗压强度，以应力比1∶0.5∶-0.1为例，在计算情况下，三轴混凝土抗压强度降低为单压的38%，抗拉强度也降低为单拉的36%。不管是拉压压状态还是拉拉压状态，随着侧向拉应力的增加，混凝土抗压强度降低的速度表现出了明显的前高后低现象。当σ1/σ3在-0.4～0.0之间时，混凝土强度迅速降低；当σ1/σ3<-0.4后，混凝土强度速度有所放缓。大体数据见表2。

表2 混凝土三轴拉压试验强度汇总

与三轴压缩试验相比，在三轴拉压试验中，第二主应力σ2对混凝土强度的影响要大于三轴压缩试验(见图10)。在同一个σ1/σ3情况下，随着σ2/σ3从0.0到1.0，混凝土的抗压强度先升高后降低，最大抗压强度一般出现在σ2/σ3=0.4～0.5之间，当σ2/σ3趋向于σ1/σ3，即趋向于压缩子午线，混凝土抗压强度降低比较明显，最大幅值达43%；当σ2/σ3从0.5左右趋向于1.0，即趋向于拉伸子午线时，混凝土的三轴强度亦有所降低，但降低幅度一般不大，最大幅值不超过同一σ1/σ3的最高强度的15%，个别试验点出现较大降幅，不排除是由于试验本身的原因。整体上看，当σ2/σ3从0.5左右趋向于1.0，混凝土的三轴强度降低属于微幅调整范围。

根据以上试验分析成果，为了更加方便地利用混凝土试验结果，并充分考虑侧向主拉应力对混凝土强度的影响以及第二主应力对混凝土强度的影响，对图10的成果做了充分的简化(见图11)。首先是以σ1/σ3作为主要分类指标，给出了不同σ1/σ3情况下混凝土强度比值，在数值的整理中采取了安全偏保守的原则，归纳值显著低于试验值；其次，以σ1/σ3=0.4为界限，当σ1/σ3>0.4时忽略中间主应力的影响，以水平直线对成果进行简化，当σ1/σ3<0.4时，针对不同σ1/σ3的情况，采用不同的斜率，以斜直线的形式对试验成果进行简化。最终的结果如图11所示。

三轴受拉状态比较复杂，国内外试验的结果离散性较大，规律性较差，同时在拱坝设计中一般不可能出现三轴受拉的应力组合状态，因此本文对这种应力状态不予阐述。

3.3 查图算法

根据拱坝拱梁分载法或线弹性有限元计算成果，可获得拱坝结构任意一点的应力状态及主应力比，分三轴受压状态或三轴拉压状态，根据图9或图11进行插值，即可得出相应部位混凝土的抗压强度比，进而获得该部位混凝土的真实强度。根据真实强度与拱坝实际应力的比值，即可获知任意点的真实点安全度，进而进行开裂危险性判断。各种算例的计算成果表明，拱坝的实际点安全度与规范推荐的名义安全度4.0之间存在巨大差异，尤其是拱坝下游侧靠近建基面区域，由于有可能处于拉压状态区，其真实点安全度下降明显，局部趋近于1.0。

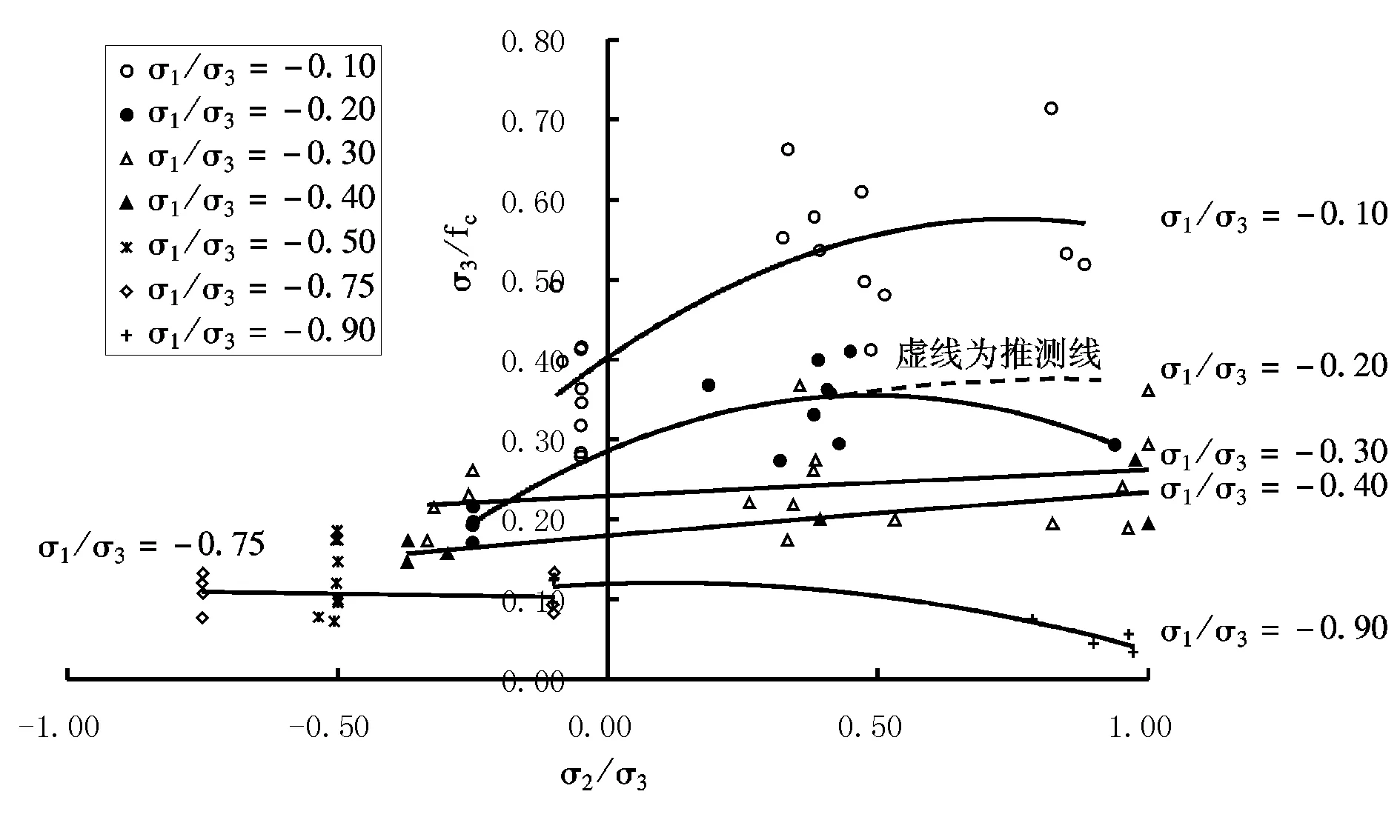
图10 三轴拉压状态下混凝土抗压强度曲线

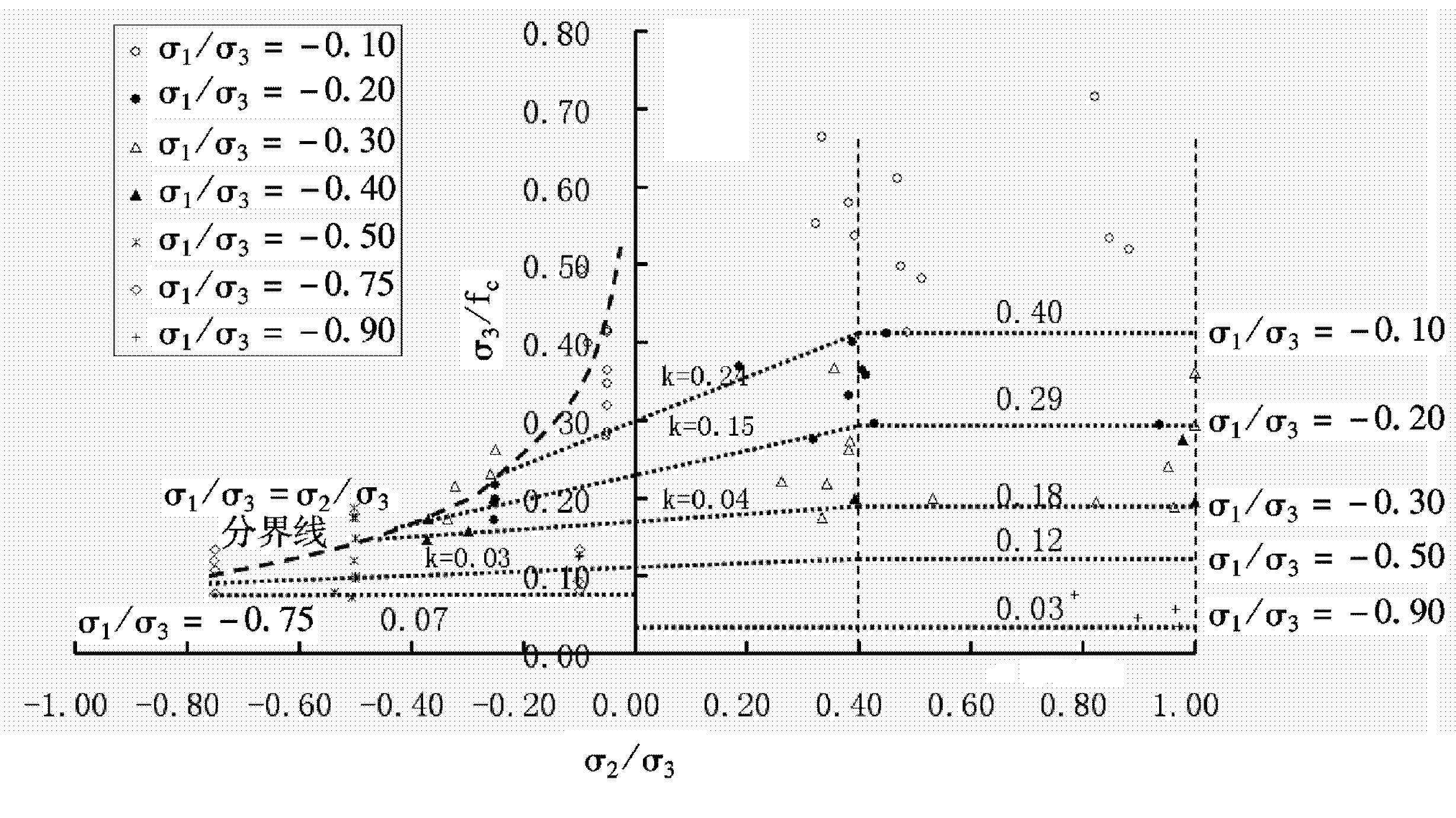
图11 三轴拉压状态下混凝土试验简化成果曲线

4 二滩拱坝开裂实例分析

二滩拱坝最大坝高240m，为抛物线型双曲拱坝，拱冠顶部宽度11.0m，底部宽度55.74m，拱端最大宽度58.51m，厚高比0.232，拱圈最大中心角91.5°，坝顶弧长744.69m。

自2000年12月份起，陆续在拱坝下游面发现多条裂缝，至2005年12月，共计发现细微裂缝127条，裂缝主要集中在拱坝右岸下游面，以发丝状裂缝为主，有两条较长，垂直于建基面起裂，延伸一定长度后逐渐转为水平裂缝。其右岸下游侧裂缝素描如图12所示[13]。

本文采用线弹性有限元对二滩拱坝结构受力进行了分析。为了突出拱坝强度的影响，分析中不考虑温度荷载以及右岸下卧的软弱条带的影响。此外，根据二滩混凝土试验成果，本文选用φ45cm×90cm圆柱体试件试验强度模拟大体积全级配混凝土的真实强度。根据试验总结和国内外大量资料，取用的混凝土尺寸效应换算关系如下：

Rφ45×90=0.69Rc20

(2)

线弹性有限元计算结果显示，在拱坝的下游面，最大主压应力出现在坝趾部位，最大值约为9～10MPa。下游面坝体中上部，从建基面往拱坝内侧延伸，存在一个宽条状拉应力带，但量值很低，基本接近于0，最大拉应力约0.2MPa。由于该区域拱坝压应力亦较小，所以拉压应力比较大，属于较为危险的区域。从中间主应力的分布来看，中间主应力基本为压应力，数值在2MPa以内，因此，整个下游坝面为明显的三轴压缩应力区和两压一拉应力区，无两拉一压应力区出现(见图13所示)。

图12 二滩拱坝右岸下游面坝面裂缝分布

由查图算法可知，要分析结构的真实安全度，必须知道任意一点的三轴主应力比值。本文计算了两类应力比：一类是最大、最小主应力应力比R1，该数值最大程度上影响了结构体的真实点安全度；另外一类是中间主应力/最小主应力所得的应力比R2，该值能客观反映中间主应力对拱坝安全度的影响。

图13 二滩拱坝下游面拉应力区

根据上节给出的主应力计算结果，分别作应力比R1和R2的等值线图(见图14、15)。由于本文限定以拉应力为正、以压应力为负，且σ1>σ2>σ3，因此在R1等值线图中，应力比一般在-1.0～1.0之间，其中在三轴压缩应力区，应力比恒为正，三轴拉压应力区恒为负。在应力比R2的等值线图中，在三轴压缩应力区，应力比恒为正，且小于1；但在三轴拉压状态，应力比有可能为正，也有可能为负，一般在一拉两压应力区应力比恒为正，在两拉一压应力区应力比恒为负值。

从应力比R1的等值线图可以看出，二滩拱坝下游坝面上部以及下部高程中间部位处于三轴压缩应力区，应力比R1为正值，但数值较小，绝大部分在0～0.2之间。两侧靠近建基面附近以及中部高程，应力比R1为负值，显示该部位处于三轴拉压状态，应力比较小，绝大部分在-0.1～0之间。根据应力比R2的等值线图，下游面应力比R2在左、右岸基本对称，且均为正值，这意味着整个下游面中主应力均为负值，即没有出现两拉一压应力区；R2值普遍较小，一般在0.0～0.3之间，最大值出现在中下部高程拱冠梁处，约为0.8左右，但大于0.4的区域范围很小。

图16是根据下游面应力比R1和R2的计算成果，考虑到大坝的取用混凝土强度，利用本文的查图算法绘制的下游面真实安全度等值线图。从图16可以看出，在拱坝下游面的中上部高程大部分区域虽然由于拉压应力状态的出现，一定程度上降低了安全系数，但这些区域应力量级较小，因此整体安全度依然较大。但是在拱坝中上部高程右侧靠近坝肩的部位，以及左岸相同部位，出现了较小范围的低安全系数区，局部安全系数最低接近于1.0。结合前文提到的拉应力区分布，进一步说明，在三轴拉压状态混凝土的安全系数比单轴应力计算的结果低，采用单轴强度准则设计方法在拉压应力区是偏于危险的。同样，在拱坝中下部靠近建基面附近，由于该部位压应力较大，少量的拉应力就极大削弱了结构的安全系数，从安全系数等值线看，该部位最小安全系数在2.0～3.0之间。由于本文有限元计算成果还没有反映温度应力的影响，没有反映地质结构的影响，如果考虑上述影响，很有可能导致安全系数的进一步降低，因此这意味着该区域存在较大的开裂危险性。这一计算结果，是与拱坝实际开裂部位相互吻合的。

图14 二滩拱坝下游面应力比R1等值线

图15 二滩拱坝下游面应力比R2等值线

图16 二滩拱坝下游面安全系数

5 结 论

本文提出了一套简单实用的评价混凝土多轴强度下结构体安全系数的算法，并对二滩拱坝下游面的坝面开裂进行了分析，得出以下一些基本结论：

(1)当混凝土处于多轴拉压状态，混凝土的强度低于单轴强度，这种情况下如采用混凝土单轴强度准则设计多轴拉压状态的混凝土结构将是偏于不安全的。而当混凝土处于多轴受压状态，混凝土的强度将高于单轴强度，此时如采用混凝土单轴强度设计，就会使整个结构的设计偏于保守，浪费材料。

(2)在混凝土的多轴强度中起关键作用的是最大、最小主应力比，中间主应力也影响结构的强度，但不起主要作用。统计表明，拉压组合状态下，当最大、最小主应力比为0.1时，混凝土的抗压强度将下降为单轴强度的38%～65%；当最大、最小主应力比为0.2时，混凝土的抗压强度将下降为单轴强度的10%～40%。抗拉强度亦有大致相同比例的降低。

(3)文中根据试验规律总结了一套简单实用的查图算法，可以根据结构应力计算成果较为方便地估计当前结构体的点安全系数。该法简单实用，可以为工程提供大致参考。当然方法本身依赖于应力计算的准确性。

(4)就拱坝点安全系数而言，在三轴压缩应力区，由于混凝土强度得到有效加强，绝大部分区域安全系数均可以达到5.0以上。但在三轴拉压应力组合区，由于拉压组合效应的存在，混凝土点安全系数显著降低，局部甚至接近于1.0。从分布来看，一般拱坝上游面离开建基面5m以上的区域安全系数均大于5.0。靠近上游拱坝建基面5m范围的窄条带内，由于应力集中，有可能出现安全系数急剧降低的现象。尤其在坝踵部位，由于竖向拉应力以及横河向较高压应力的存在，安全系数降低非常明显，局部接近于1.0。而对于下游面，靠近拱坝建基面20m范围的宽条带内，有可能出现拉压应力组合区，但这些部位应力量级不是很大，所以安全系数会削减但不很突出，一般在2.0～5.0之间。

(5)二滩拱坝的计算表明，在下游面中部高程区域靠近建基面附近，存在大片的低安全系数区，并有向中部高程内侧延伸的趋势，最低安全系数接近于1.0，尤其在拱坝下游面右岸，安全系数的削弱更加明显。由于本文没有考虑地质结构面和温度应力的影响，软弱夹层通过改变相应高程的变形模量实现，因此当考虑寒潮等不利温度条件以及考虑地质结构面时，有可能产生更低的安全系数，而这些区域与目前拱坝下游面开裂的部位大致相同。这说明拱坝自身结构在拉压组合状态下混凝土强度的降低有可能是引发二滩拱坝下游面裂纹的主要因素之一。

[1] 周元德．混凝土非线性断裂力学模型与高拱坝开裂分析研究[D].北京：清华大学水利水电工程系，2004.

[2] 宋玉普.多种混凝土材料的本构关系和破坏准则[M].北京：中国水利水电出版社，2002.

[3] 王敬忠.三轴拉压强度试验和混凝土破坏准则的研究[D].北京：清华大学，1989.

[4] 叶献国.三轴受压混凝土的强度与变形试验研究[D].北京：清华大学，1988.

[5] 揽生瑞.复杂应力史下混凝土本构关系的试验研究[D].北京：清华大学，1994.

[6] 曲俊义.二轴三轴应力下混凝土强度的试验研究[D].北京：清华大学，1985.

[7] 郭玉涛.二轴应力下高强混凝土强度和变形的试验研究[D].北京：清华大学，1995.

[8] 李伟政.二轴拉压应力全组合下混凝土的强度及变形试验研究[D].北京：清华大学，1989.

[9] 郑汝玫.二轴受压混凝土的强度和变形试验研究[D].北京：清华大学，1987.

[10] 过镇海.混凝土的强度和本构关系-原理与应用[M].北京：中国建筑工业出版社，2004.

[11] 电力部成都勘测设计研究院.高强度大体积混凝土材料特性研究，“八五”国家科技攻关，合同编号：85-208-01-03，1995.

[12] 张冲.多轴效应拱坝实用本构模型及二滩拱坝开裂分析研究[R].中国水电顾问集团成都勘测设计研究院，清华大学博士后研究报告，2009.

[13] 中国水电顾问集团成都勘测设计研究院，二滩水电开发有限责任公司.四川省雅砻江二滩水电站拱坝安全监测分析报告(1998-2005)[R].2007.