有限弱Y-稳定变换半群的最大幂等分离同余

冯正浩，杨秀良

（杭州师范大学理学院，浙江杭州 310036）

有限弱Y-稳定变换半群的最大幂等分离同余

冯正浩，杨秀良＊

（杭州师范大学理学院，浙江杭州 310036）

文章利用有限半群最大幂等分离同余的一般结论，首先研究有限弱Y-稳定变换半群W（Y）＝｛α∈T（X）∶Yα⊆Y｝上任意元的弱逆元，进而刻划出W（Y）上最大幂等分离同余的具体形式.

最大幂等分离同余；弱逆元；正则元

0 引 言

设T（X）为非空集合X上的全变换半群，对于X的任意非空子集Y，令

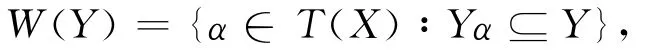
则W（Y）显然是T（X）的一个子半群，并称W（Y）为弱Y-稳定变换半群.特别地，当X为有限集时，W（Y）称为有限弱Y-稳定变换半群.1966年，Magill［1］首先对W（Y）进行了研究.随后Higgins和Umar刻划出了W（Y）上的Green关系和Green＊关系，证得W（Y）为富足半群，并且还刻划出了当X为有限集时W（Y）的核.最近，Nenthein等人［2］刻划出了W（Y）上的正则元以及等价条件，并计算出了当X为有限集时正则元的个数.此外，Nenthein和Kemprasit［3］还得到了W（Y）为BL-半群的必要条件.

令S为一个有限半群且a∈S.若S中的元x满足x＝xax，那么称x是a的一个弱逆元.记a的所有弱逆元组成的集合为WI（a）.在［4］中已经成功刻划出了S上的最大幂等分离同余，并且此种刻划是从弱逆元的角度出发的.

该文将根据此结论具体刻划出有限弱Y-稳定变换半群W（Y）的最大幂等分离同余.首先刻划W（Y）中任意元α的弱逆元，然后根据所得到的弱逆元具体形式刻划出W（Y）的最大幂等分离同余.值得注意的是W（Y）有两种特殊情况：1）当｜Y｜＝｜X｜时，有W（Y）＝T（X）；2）当1＝｜Y｜＜｜X｜时，有W（Y）≅PT（X＼Y），其中PT（X＼Y）是X＼Y上的部分变换半群.T（X）和PT（X）上的所有同余均已被构造［5］.因此下文假设W（Y）满足｜X｜＝n，｜Y｜＝k且1＜k＜n.

1 弱逆元

定理1 令α∈W（Y），则以下条件等价：

命题1 对于任意α∈W（Y），若α′为α的一个极大弱逆元，则

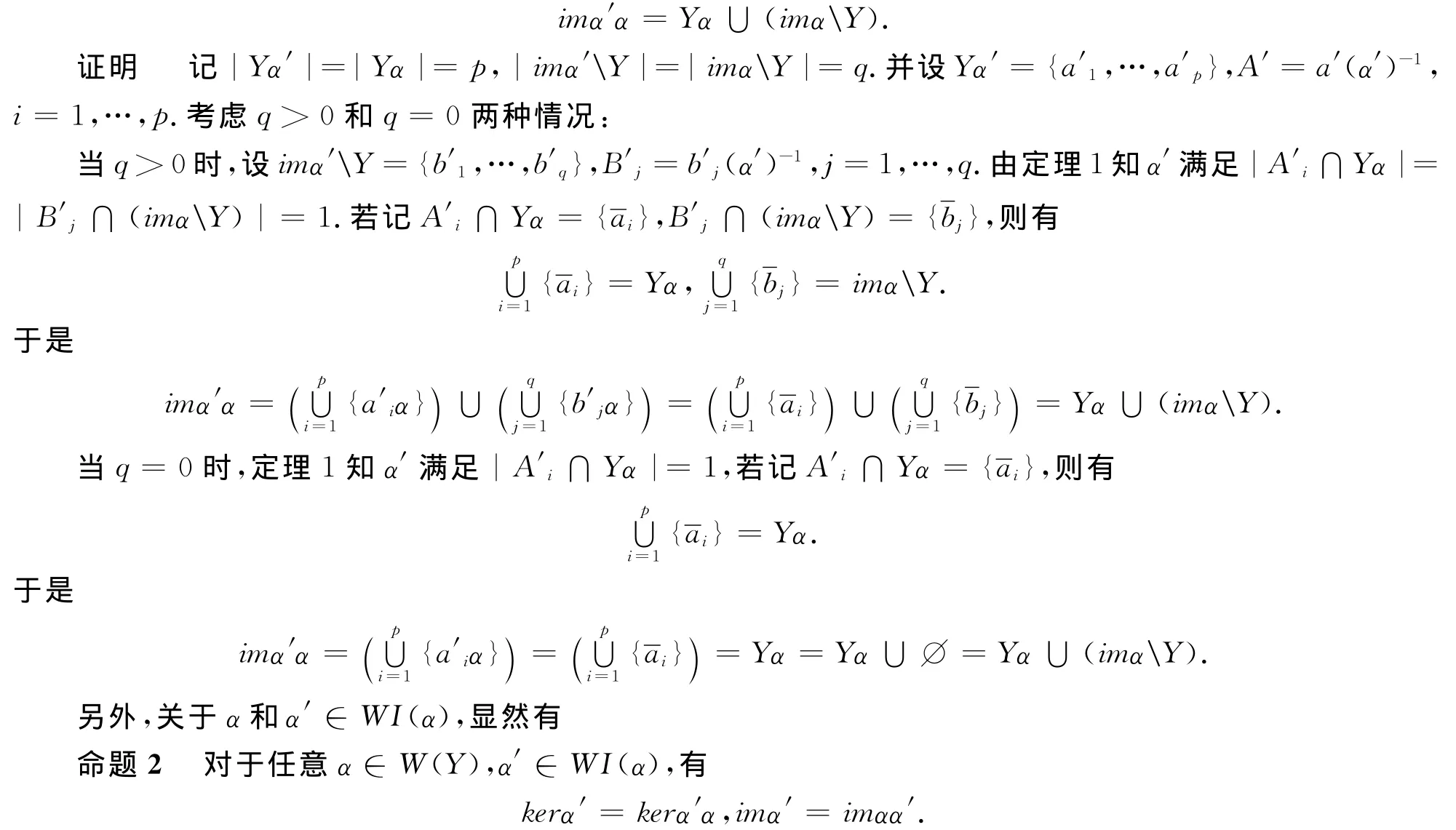
2 最大幂等分离同余

首先，由［4，定理2.6］可得：

引理1 在W（Y）上定义关系τ如下：

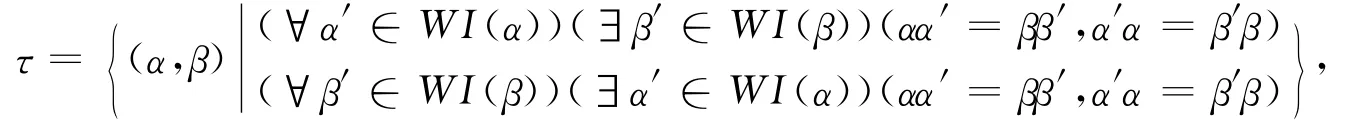
则τ是WY的最大幂等分离同余.

以下利用引理1的结论和上文得到的W（Y）中任意元α的弱逆元来尝试刻划W（Y）上最大幂等分离同余的具体形式.

引理2 若α，β∈W（Y）且ατβ，则

其中y是Y中的任意元.

定义1 在W（Y）上定义关系θ如下：

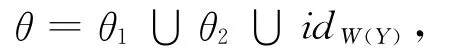
其中idW（Y）是W（Y）上的恒等关系.

定理2θ是W（Y）的最大幂等分离同余.

证明 先证τ⊆θ.

任取（α，β）∈τ，由引理2可知Yα＝Yβ，imα＼Y＝imβ＼Y.记｜Yα｜＝｜Yβ｜＝p，｜imα＼Y｜＝｜imβ＼Y｜＝q.下面对pq进行讨论：

情况1p＝1，q＝0.

此时显然有（α，β）∈θ1⊆θ.

情况2p＝1，q＞0.

运用情况2和情况3中的证明技巧，可得β＝α，于是有（α，β）∈idW（Y）⊆θ.

再证θ⊆τ.

任取（αβ∈θ.只需考虑（αβ∈θ1和（αβ∈θ2两种情况.

当（α，β）∈θ1时，有WI（α）＝WI（β）＝I1（I1为W（Y）中所有常值变换组成的集合）.则对于任意α′∈WI（α），只要取β′＝α′，显然有β′∈WI（β）且β′β＝α′α，ββ′＝αα′.而对于任意β′∈WI（β），只要取α′＝β′，显然有α′∈WI（α）且α′α＝β′β，αα′＝ββ′.故（α，β）∈τ.

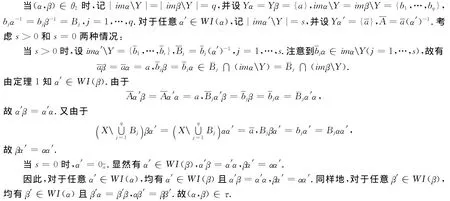
［1］Magill K D.Subsemigroups ofS（X）［J］.Math Japon，1966，11：109-115.

［2］Nenthein S，Youngkhong P，Kemprasit Y.Regular elements of some transformation semigroups［J］.PU M A，2005，16（3）：307-314.

［3］Nenthein S，Kemprasit Y.On transformation semigroups which are BL-semigroups［J］.International Journal of Mathematics and Mathematical Sciences，2006（1）：1-10.

［4］Luo Yanfeng，Li Xiaoling.The maximum idempotent-separating congruence on eventually regular semigroups［J］.Semigroup Forum，2007，74：306-318.

［5］Ganyushkin O，Mazorchuk V.Classical finite transformation semigroups：an induction［M］.New York：Springer-Verlag，2009：100-107.

The Maximum Idempotent-Separating Congruence in Finite Transformation Semigroups of WeakY-Stabilizer

FENG Zheng-hao，YANG Xiu-liang

（College of Science，Hangzhou Normal University，Hangzhou 310036，China）

Using the results of the maximum idempotent-separating congruence on finite semigroups，this paper investigated the weak inverse in finite transformation semigroups of weakY-stabilizer，which wasW（Y）＝｛α∈T（X）∶Yα⊆Y｝，and described the concrete forms of maximum idempotent-separating congruence inW（Y）.

maximum idempotent-separating congruence；weak inverse；regular element

O152.7 MSC2010：20M10

A

1674-232X（2011）03-0208-05

10.3969／j.issn.1674-232X.2011.03.004

2010-10-20

冯正浩（1985—），男，浙江湖州人，基础数学专业硕士研究生，主要从事半群代数理论研究.

＊通信作者：杨秀良（1963—），男，贵州黎平人，教授，主要从事半群代数理论研究.E-mail：yxl＠hznu.edu.cn