利普希茨空间到有界解析函数空间的加权微分复合算子*

张 亮

(天津大学 理学院，天津 300072）

利普希茨空间到有界解析函数空间的加权微分复合算子*

张 亮

(天津大学 理学院，天津 300072）

加权微分复合算子理论是算子领域的重要组成部分.不同空间的加权微分复合算子的有界性和紧致性被深入地研究并出现了许多成果.在此基础上给出了单位圆盘上从利普希茨空间到有界解析函数空间的加权微分复合算子有界和紧致的性质，并证明了算子有界和紧致的充要条件.

利普希茨空间;有界解析函数空间;加权微分复合算子

引言

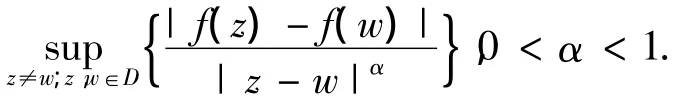
设φ∈H(D)，记Cφ为H(D)上的复合算子:Cφf(z)=f(φ(z))，z∈D ，f∈H(D).设D为H(D)上的微分算子:Df(z)=f'(z).H(D)上的加权微分复合算子uCφD定义为:uCφDf(z)=u(z)f'(φ(z)).

范数A与范数B等价，记:A≈B，如果存在常数C＞0，使得B/C≤A≤CB.

文献［1～5］已经深入研究了微分复合算子在不同空间的有界性和紧致性.借助文献［1～5］的一些方法，给出了从利普希茨空间到有界解析函数空间的加权微分复合算子的一些性质.

1主要引理

引理1［6］设X和Y是Λα或者H∞β空间，则算子uCφD:X→Y是紧算子，当且仅当uCφD:X→Y为有界算子且对任意有界序列{fk}⊂X，当k→∞ 时，若{fk}在单位圆盘的紧子集上一致收敛于0，则uCφDfk在Y上也一致收敛于0.

引理2［7］如果0 ＜ α ＜ 1，则B1－α(D)= Λα(D);且任意的f∈ Λα(D)有:

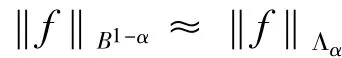
2 主要定理及其证明

定理1 假设0＜α＜1且φ是单位圆盘上的解析自映射，u∈H(D)，则uCφD∶Λα→H∞β是有界算子当且仅当

证明 微分复合算子有界的充分性证明如下:

假设条件(1)成立，则对任意的z∈D且f∈Λα，

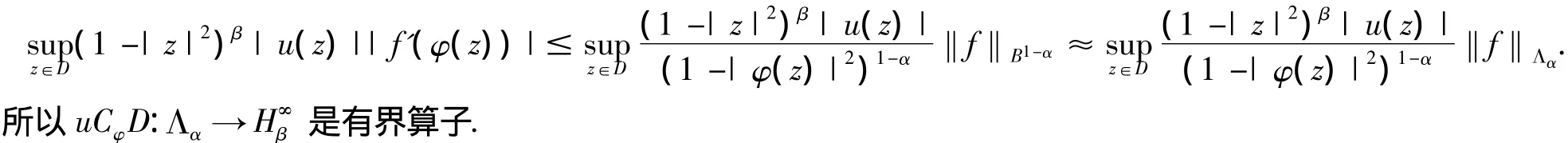
微分复合算子有界的必要性证明如下:

假设uCφD:Λα→H∞β是有界算子，则对所有f∈ Λα，存在常数C，使得 ‖uCφDf‖H∞β≤C‖f‖Λα.则令f(z)=z，有:

证明 微分复合算子是紧算子的充分性证明如下:

假设uCφD:Λα→H∞β有界且式(8)成立，设{fk}k∈N是Λα上的序列满足sku∈p∈N‖fk‖Λα＜ ∞，且当k→∞ 时，fk在D的紧子集上一致收敛于0.由假设，对任意的ε＞0，存在δ∈(0，1)，使得下式成立，即:

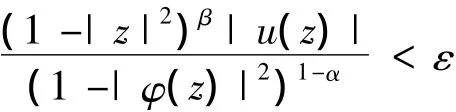
设K={z∈D:|φ(z)|≤δ}，结合引理2，则有:

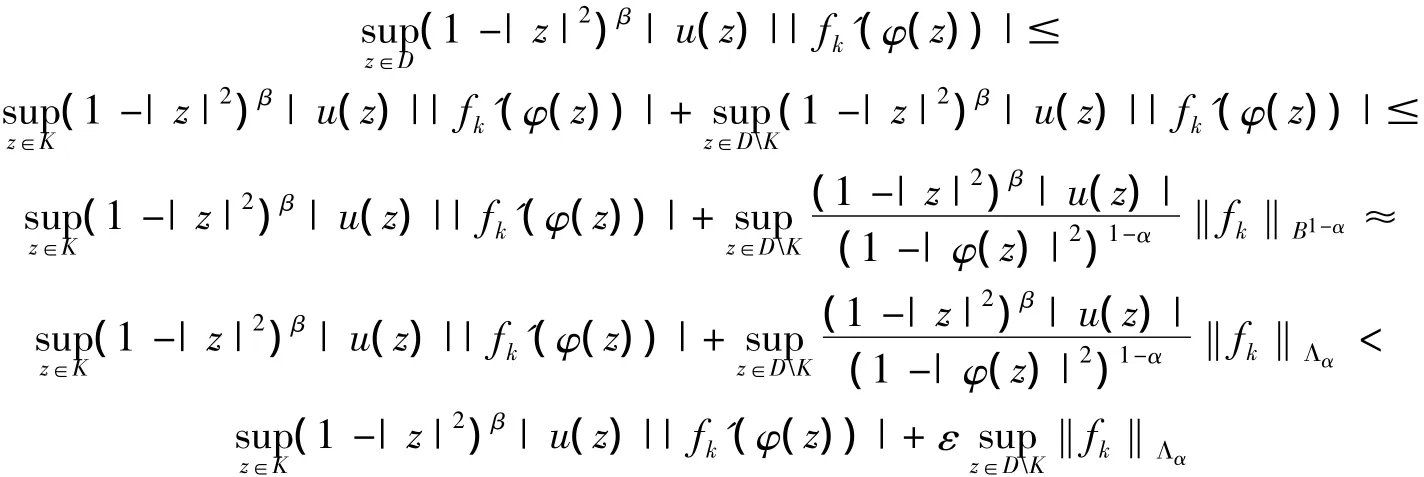
微分复合算子是紧算子的必要性证明如下:

假设uCφD是紧算子，则uCφD是有界的.设{zk}k∈N是D上的序列且当k→∞ 时，|φ(zk)|→1.设:

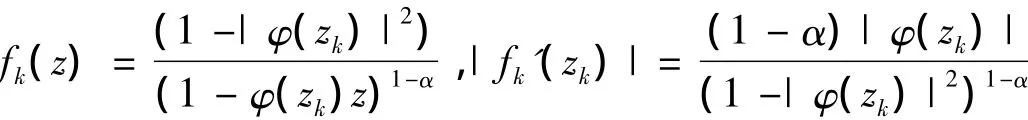
易证fk∈Λα，sku∈pN‖ fk‖Λα＜∞，且当k→∞ 时，fk在D的紧子集上一致收敛于0.

因为uCφD是紧的，由引理1，klim→∞‖uCφDfk‖H∞β=0.所以:

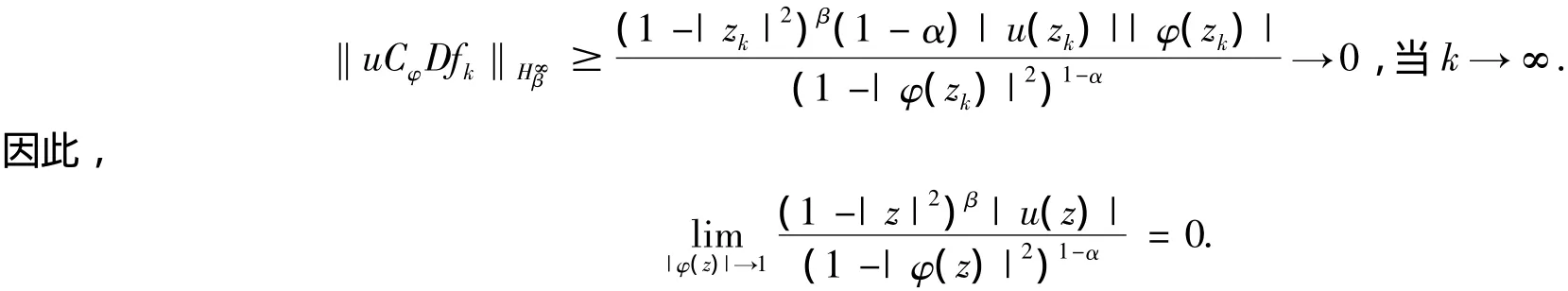
［1］Stevi'c S.Norm of weighted composition operators from Bloch space to on the unit ball［J］.Ars Combinatoria，2008，88:125–127.

［2］Stevi'c S.On a new operator fromto the Bloch －type space on the unit ball［J］.Utilitas Mathematica，2008，77:257 －263.

［3］Wulan H ，Zhou J.Type spaces of analytic functions［J］.Journal of Function Spaces and Applications，2006，4(1):73 －84.

［4］Zhou Z H，Shi J H.Compactness of composition operators on the Bloch space in classical bounded symmetric domains［J］.Michigan Math，2002，50:381－405.

［5］Hu Z，Wang S.Composition operators on Bloch－type spaces［J］.Proceedings of the Royal Society of EdinburghA，2005，135(6):1229－1239.

［6］Cowen C C，MacCluer B D.Composition operators on spaces of analytic functions［M］.CRC Press，Boca Raton，FL，1995.

［7］Zhu K H.Spaces of holomorphic functions in the unit ball［M］.New York:Springer，2005.

Abstrac:Theories of weighted differentiation composition operators are important component parts in operator fields.Boundedness and compactness of the weighted differentiation composition operators between different spaces have been widely studied and a number of results have been given.On this basis，the necessary and sufficient conditions of the boundedness and compactness of the weighted differentiation composition operator from the Lipschitz spaces to bounded analytic function spaces in the unit disk are presented and proved.

Weighted Differentiation Composition Operators from Lipschitz Space to Bounded Analytic Function Space

ZHANG Liang

(Institute of Sciences，Tianjin University，Tianjin 300072，China)

Lipschitz spaces;bounded analytic function spaces;weighted differentiation composition operators

O 174.5

A

1673－2103(2011)05－0025－03

2011－06－08

国家自然科学基金资助项目(10971153);国家自然科学基金资助项目(10671141)

张亮(1983－)，男，山东德州人，在读硕士研究生，研究方向:多复变函数和算子理论及其应用.