参保职工年龄结构变动测算模型构建及应用

马 伟，王立剑

(西安交通大学 a.公共政策与管理学院;b.人文社会科学学院，陕西 西安 710049)

●实务·方法

参保职工年龄结构变动测算模型构建及应用

马 伟a，b，王立剑b

(西安交通大学 a.公共政策与管理学院;b.人文社会科学学院，陕西 西安 710049)

参保职工年龄结构变动直接影响社会保险基金的收支，文章采取“反馈式”人口年龄结构测算思路，对人口发展方程进行改进，进而构建参保职工年龄结构变动测算模型;以苏州工业园区公积金会员年龄结构变动为例的实证研究表明，公积金会员年龄结构呈跳跃式发展，60岁以上会员占总人数的比例到2050年达到最高值47．3%，抚养比由636∶1下降到2050年的1.13∶1，进而证明了模型的有效性。

参保职工;年龄结构;测算模型

一、引 言

21世纪上半叶，我国人口结构将发生老龄化、高龄化等变动，直接影响社会保障需求与供给［1］。社会保险参保职工是总人口的一部分，其年龄结构随着总人口年龄结构的老龄化过程而趋于老化，但两者老龄化进程和特征又因参保职工的人口学特殊性而不同。参保职工年龄结构对社会保险基金收支及其缺口的影响更为直接:在职参保职工的缴费是社会保险基金收入的主要来源;退休或遭遇社会风险的参保职工是社会保险基金支出的主要对象，二者数量和比例的变化直接影响到社会保险基金的收入和支出。在我国社会保险制度面临巨大财务可持续性危机的背景下，准确测算参保职工年龄结构的未来变动趋势，对于精算社会保险基金的收入、支出、缺口以及财政补贴规模，进而未雨绸缪，保证社会保险事业的可持续发展具有重要的基础理论意义。

人口年龄结构是指一定时点、一定地区各年龄组人口在全体人口中的比重［2］。相应的，参保职工年龄结构是指一定时点、一定地区各年龄组参保职工人数在全体参保职工总数中所占的比重。关于人口年龄结构变动的测算方法、模型研究已经较为成熟，但是，很少有学者将研究的视野确定为参保职工年龄结构。年龄移算模型、凯菲茨矩阵方程模型、莱斯利矩阵预测模型、宋健人口发展方程、王广州系统仿真结构功能模型［3］、系统工程［4］、BP 神经网络技术［5］、非线性年龄结构种群最优控制动力学模型［6］、特征曲线法、有限差数法［7］等模型和方法都曾被应用于人口年龄结构变动测算领域。John W.Peabody［8］等系统地阐述了COPD模型在分年龄组人口预测方面的应用;Laurence S.Seidman［9］运用时间序列方法对社会保障体系中的退休人员数量进行预测，这种预测方法在国内应用较为普遍;李永胜［10］介绍了进行人口年龄结构预测模型选择和参数设定的方法和原则;门可佩［11］建立灰色动态预测模型对中国未来50年的人口进行预测。在关于人口年龄结构对养老保险基金收支影响的研究中，刘贵平［12］以全国范围内的人口出生率和死亡率为基础，研究劳动年龄人口的变动对养老保险的影响。但是，他的研究是基于全国人口数据资料，而不是制度覆盖范围内的人口数据资料，缺乏针对性。

本文采取“反馈式”人口年龄结构变动测算思路，对人口发展方程进行改进，进而构建参保职工年龄结构变动测算模型;以苏州工业园区公积金会员年龄结构测算为例，对模型进行应用性研究，证明模型的可操作性。

二、模型构建

(一)前提假设

本文以l岁作为年龄组距，分别计算各年龄组的参保职工人口数，以表明参保职工年龄结构状况。由于参保职工一般是超过17岁的有稳定收入的人群，且在这一群体中的“出生率”、“死亡率”等变量具有一定的特殊性，因此，在构建模型之前，本文作出如下假设:

(1)参保人统称为参保职工。根据《社会保险费征缴暂行条例》，参加社会保险的人员包括国有企业、城镇集体企业、外商投资企业、城镇私营企业和其他城镇企业及其职工，事业单位及其职工，城镇个体工商户、纳入社会团体及其专职人员、民办非企业单位及其职工以及有雇工的城镇个体工商户及其雇工。我国当前社会保险制度的参保人已经突破企业职工的界限，已有郑州、重庆等地推行了居民社会保险制度，本文建设参保职工是参保人的统称。

(2)新增参保职工人数是实际新参保人数与退保人数的差值。由于在社会保险制度框架下，参保职工除因死亡原因退出参保范围外，还将受到迁移、自愿断保等现象，导致参保职工人数减少，为了计算方便，本文在新增参保职工人数中划出与除死亡原因为退保人数相等的一部分，不作为新增参保职工。

(二)构建思路

以特定时点的参保职工年龄结构数据为基础，本文首先对目标区间内的参保职工总人数进行预测，进而以年龄推移方法和新增人口、退出人口的经验规律为基础改进人口发展方程，用参保职工总人口数反馈影响人口发展的计算过程，得出参保职工年龄结构变动结果。具体而言，模型构建的思路是:

(1)预测未来参保职工的总人数。根据某区域发展的人口承载力和经济承载力规划，设定该区域总人口数的上限值;运用Logistic回归模型，对往年的参保职工数进行参数估计，得出参保职工总人数的预测模型，并进行预测。

(2)计算现有参保职工的人口发展情况。根据现有参保职工年龄结构数据，运用西安交通大学人口与发展研究所根据2000年第五次全国人口普查数据推算的分性别人口生命表，计算今后各年参保职工的死亡人数和存活人数。

(3)计算参保职工净增加总数。参保职工净增加总数是预测的参保职工总数与参保职工留存数的差值，这部分人口实际上是进入制度人口与退出制度人口的差值。

(4)计算下一年的参保职工年龄结构。根据社会调查数据和历史经验数据得出新增参保职工在每一岁男性和女性的人数占原男性和女性参保职工总数的比例，进而得到新增参保职工在性别和年龄两个纬度的分配矩阵，此矩阵与留存矩阵相加得到下一年的参保职工年龄结构。

(三)模型推导

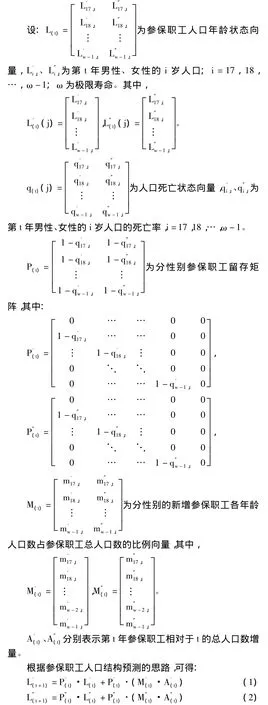
M(t)(j)可根据新增参保职工的性别比例、新增参保职工的年龄构成计算得到。公式 (1)和公式 (2)就是“反馈式”参保职工年龄结构预测模型。

三、参数设定

本研究以苏州工业园区公积金会员年龄结构为例进行实证研究。选择苏州工业园区公积金会员年龄结构为例的理由是:(1)“反馈式”参保职工年龄结构预测模型的应用对经验数据要求较高。其中，新增参保职工和退保参保职工的年龄结构需要通过实地调查采集样本数据获得，且鉴于苏州工业园区社会保障信息化程度较高，本文选取作者所在课题组进行过问卷调查的苏州工业园区为例。(2)苏州工业园区公积金会员年龄结构具有较强的代表性。苏州工业园区公积金制度分为A、B、C三类，且三类之间可以相互转化，这一运作机制与社会保险分为五大险种、参保职工不一定全部参加五大险种类似，且更加直观明了。(3)苏州工业园区公积金会员年龄结构预测更具有现实意义。苏州工业园区公积金会员年龄结构呈年轻型，它何时向老年型过渡对于苏州工业园区公积金制度发展具有决定性作用，且学术界对苏州工业园区公积金会员年龄结构尚未进行科学的预测，因此，以此为例更具有现实意义。由于苏州工业园区公积金制度分为A、B、C三类保障计划，因此，本文在公式 (1)和公式 (2)中加入表示参保类型的变量j，即

(一)测算区间

本研究预测的区间为2009—2050年，共42年。主要是因为在这一区间内，现有的公积金会员都能够达到退休年龄，即现在17岁的会员正好达到退休年龄，进入退休的行列;此外，为了保证预测的精度，不宜预测时间过长。

(二)参数预设

(1)公积金会员年龄状态向量L(t)(j)。在公积金会员年龄结构预测中，为了提高预测的精度，所使用的基础数据应该是2008年12月31日的数据，即以2008年底的会员年龄结构作为预测的基础数据。

(2)积金会员死亡率状态向量q(t)(j)。西安交通大学人口与发展研究所根据2000年第五次全国人口普查数据测算了分性别从业人口的生命表，本研究借用这一生命表，作为公积金会员死亡状态向量。

(3)2008—2050年公积金会员总数预测。Logistic人口增长模型的基本形式是:

其中，L(t)表示t年的总人数;Lmax表示人口总数的上限;t表示时间。

根据苏州工业园区经济规划及园区环境承载力得到园区从业人员的上限是120万人，即公积金会员总数的上限值是120万人。

令1997年时，t=1;1998年时，t=2;依此类推，运用1994—2008年的苏州工业园区历年公积金会员人数对公式(5)中的参数进行估计，可得:

R2=98.5%，模型具有较好的拟合优度。根据公式 (6)可以计算2009—2050年苏州工业园区公积金会员总人口数。

(4)新增公积金会员分性别、分账户、分年龄分布M(t)(j)。新增公积金会员包括两部分:一是次年的公积金会员总数与基年公积金会员总数的差值;二是基年公积金会员的死亡人数。两个值相加即为新增加的公积金会员数量。

假设新增的公积金会员按照2004—2008年各账户公积金会员数占总会员数比例的平均值于A、B、C三类账户中分配，即A类公积金会员新增人数占新增会员总人数的62.5%;B类公积金会员新增人数占新增会员总人数的24.28%;C类公积金会员新增人数占新增会员总人数的13.47%。

同样，对于新增公积金会员的性别比例也是按照经验数据获得，即A类公积金会员新增人数中，男性占53.25%，女性占46.75%;B类公积金会员新增人数中，男性占51.21%，女性占48.79%;C类公积金会员新增人数中，男性占43.79%，女性占56.21%。

为了得到新增公积金会员的年龄结构数据，对974名公积金会员进行了问卷调查，选择其中参加公积金制度1年以内的公积金会员年龄作为分析对象，进行频数分析可以看出，新增的公积金会员年龄集中在40岁以下，40岁以上人口所占比例较小，且不规则，新增公积金会员分布于40岁以上属于小概率事件，本研究将这些发生可能性较小的事件忽略。假设2009—2050年新增公积金会员的年龄结构遵循2004—2008年的分布，那么，结合分账户、分性别、分年龄的比例分配情况，可得新增公积金会员分配比例。

其统计数据见表1。

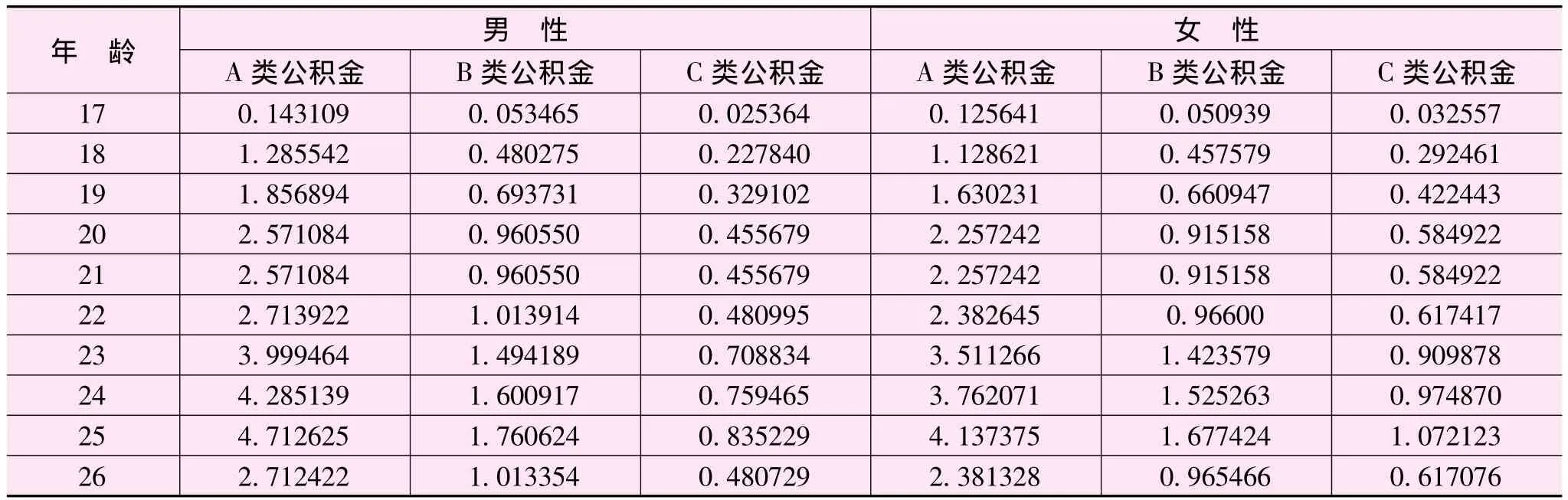
表1 新增公积金会员分配百分比统计表 (%)

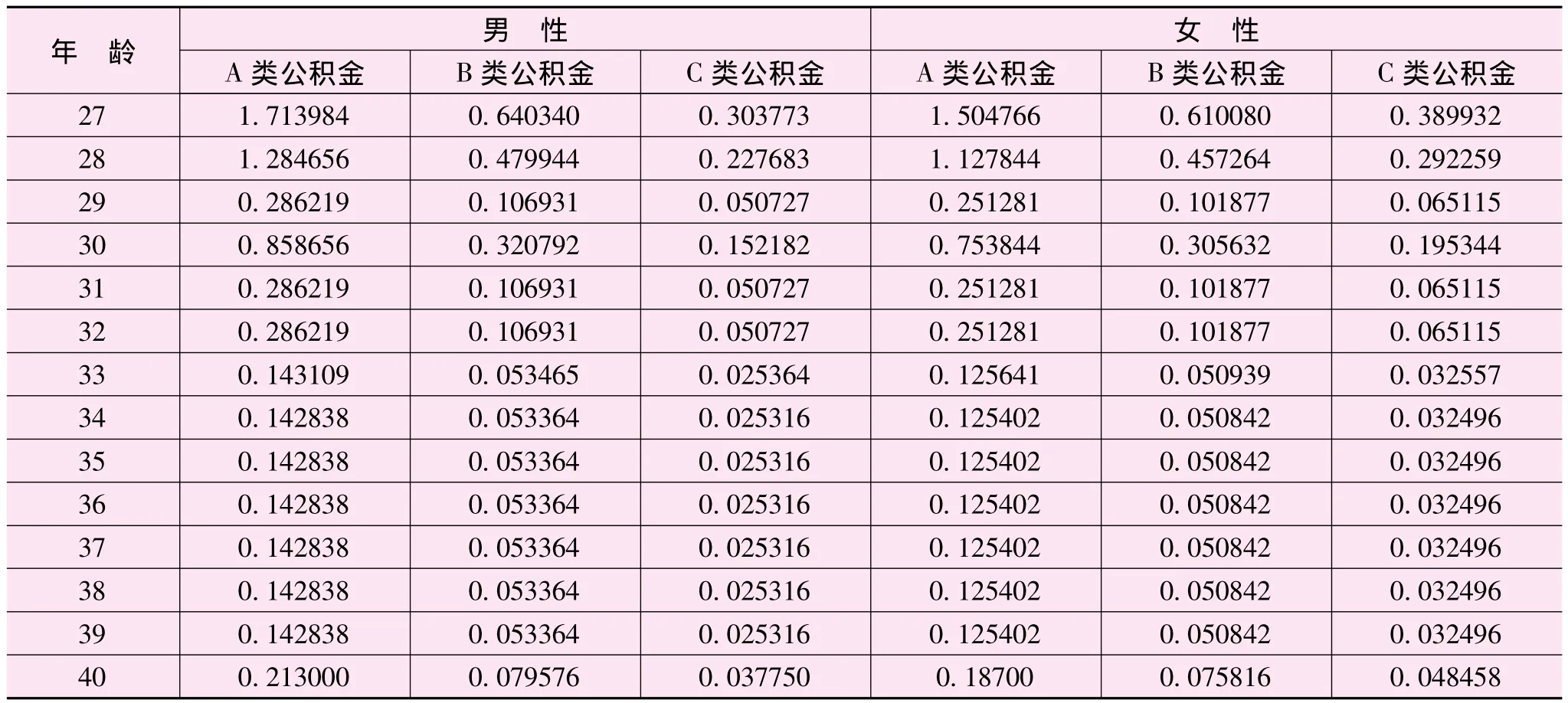
续表1

四、结果分析

根据公式 (3)和公式 (4)，以及参数设定的结果，运用Matlab6.5进行了运算计算得到2009—2050年苏州工业园区公积金会员的年龄结构。由于涉及数据较多，本文只列出2009、2022、2036、2050年四个年份的公积金会员年龄结构数据，见表2。

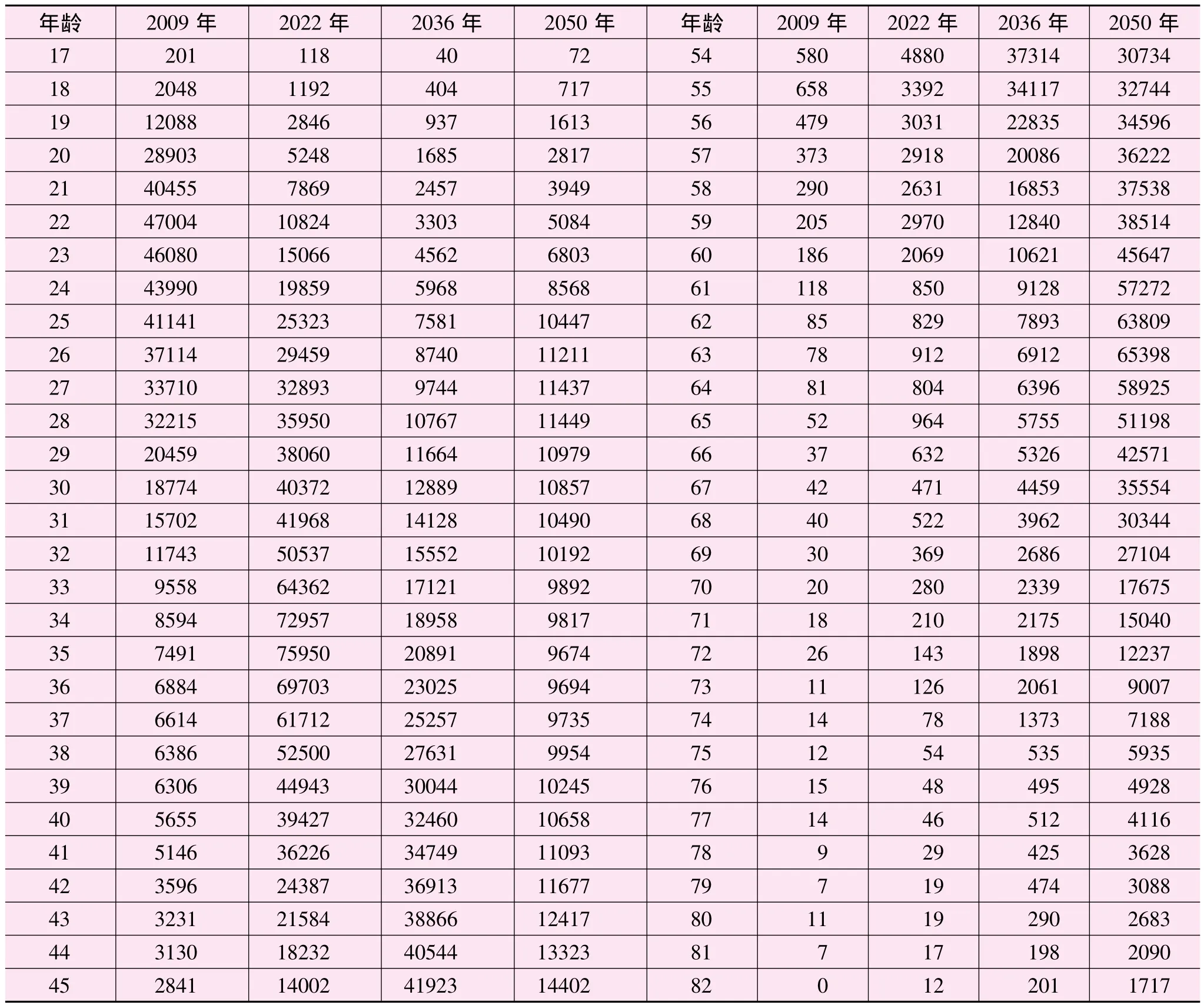
表2 公积金会员年龄结构统计表 (人)

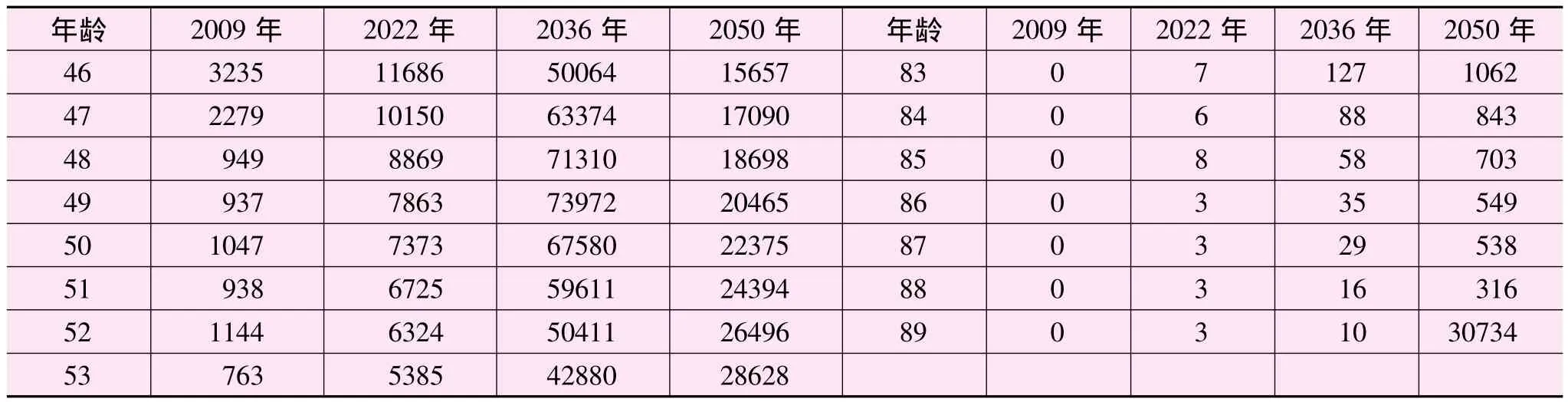
续表2

2009、2022、2036、2050年的公积金会员年龄结构的对比可以由图1直观的表示。

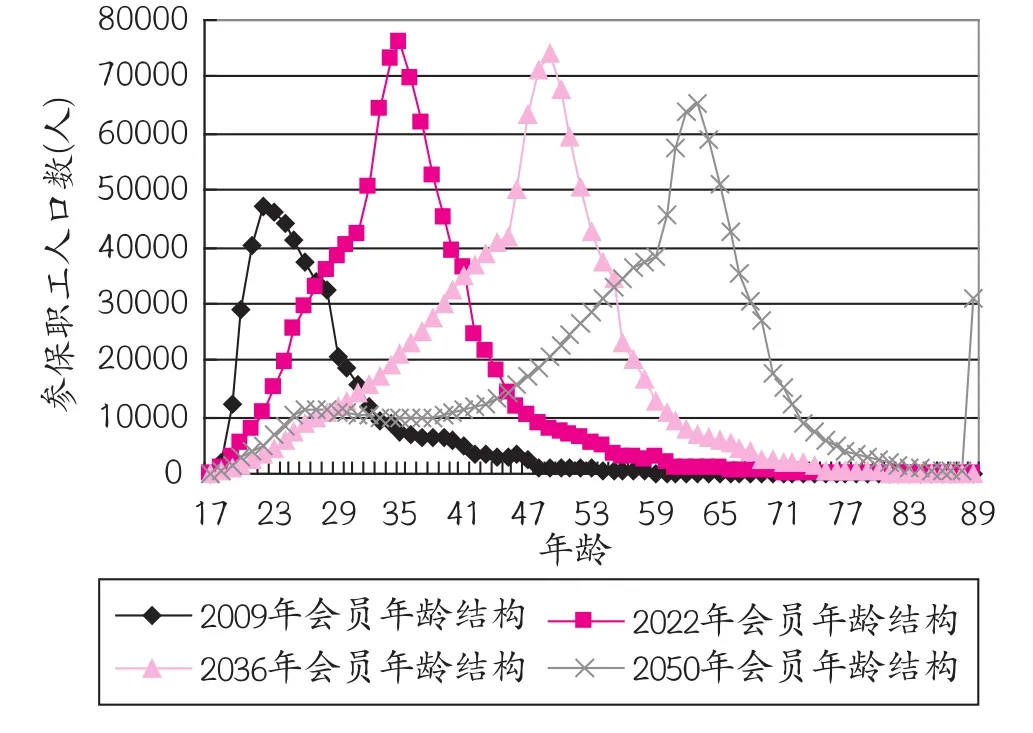
图1 公积金会员人口年龄结构示意图

由表2和图1可知，苏州工业园区的公积金会员年龄结构呈跳跃式发展。这可以由两个指标来体现:一是60岁以上人口占总人数的比例;二是抚养比，即17—59岁人口总数与60岁及以上人口数的比值。

60岁以上人口占总人数的比例说明苏州工业园区公积金会员老龄化的速度是逐渐加快的。到2037年60岁及以上人口所占比例达到9.8%，从2038年开始正式进入到老龄化社会，到2050年达到最高值47.3%。工业园区公积金会员人口老龄化的高峰并不在常规的2030—2034年，这是由于源源不断的年轻人口的流入，使得人口老龄化没有过早爆发，而一旦爆发将是一个极具爆发的过程，从2037年开始，园区老龄化经历了一个跳跃式的发展过程，从9.8%急剧增长到47.3%，这主要是因为现在的公积金会员集中在19—38岁，这部分人在2037年将集体达到或接近60岁，引起了老龄人口比例的急剧增长。

抚养比反映了苏州工业园区公积金基金的未来压力。当前，苏州工业园区公积金会员的抚养比为636∶1，随着时间的推移，越来越多的会员进入到老年人口行列，使得抚养比急剧下降。2008—2033年的抚养比下降最快，从636∶1下降到21∶1，之后下降的速度有所减缓，到2044年为3∶1，到2050年降低到1.13∶1。抚养比的降低说明公积金基金供给与需求的逐渐失衡，尤其是到2040年以后，公积金需求急剧增大，势必带来基金缺口的迅猛增长。

五、结 论

参保职工是总人口的组成部分，但它的年龄结构变动规律与总人口年龄结构变动规律有所差异，本文采取反馈式的人口结构测算思路，构建参保职工年龄结构测算模型，并以苏州工业园区公积金会员年龄结构为例进行了实证研究，证明了模型的有效性。本文采用的“反馈式”测算思路对于解决开放式的人口预测问题具有一定的借鉴意义，但这一测算方法对经验数据要求较高，尤其是需要新增和退出人口的年龄别人口数，这也对现行社会保险信息化建设提出了新的要求。

［1］王立剑，刘佳．统筹城乡的人口预测模型构建与应用［J］．西北人口，2009，30(3):24－28．

［2］佟新著．人口社会学 ［M］．北京:北京大学出版社，2003:77．

［3］李永胜．人口预测中的模型选择与参数认定 ［J］．财经科学，2004，(2):32－34．

［4］李树茁，刘晓兵．系统工程在人口研究中的应用 ［J］．西安交通大学学报 (社会科学版)，2006， (5):41－47．

［5］尹春华，陈雷．基于BP神经网络人口预测模型的研究与应用 ［J］．人口学刊，2005，(2):32－38．

［6］ Brander J A，Dowrick S．The Role of Fertility and Population in Economic Growth－Empirical Results from Aggregate Cross－National Data［J］．Journal of Population Economics，1994，(7):1 －14．

［7］ Bloom DE＆D Canning．Demographic Change and Economic Growth in Asia［J］．Population and Development Review，2000，(8):58．

［8］ John W．Peabody，COPD:A prevalence estimation model［J］．The Economic Journal，2006，2:134 －138．

［9］ Laurence S Seidman，Forecasting the Number of Social Security Retirees:Improving Forecasts for Better Policy Making［M］．Blackwell Publishing Ltd，2003:15－19．

［10］李永胜．人口预测中的模型选择与参数认定 ［J］．财经科学，2004，(2):68－72．

［11］门可佩．中国未来50年人口发展预测研究 ［J］．数量经济技术经济研究，2004，(3):24－30．

［12］刘贵平．人口变化与我国城镇职工养老保险 ［J］．人口学刊，2000，(4):31－33．

Actuarial Models of Age Structure Changes of Workers Participating in Pension Insurance System and Its Application

MA Weia，b，WANG Li-jianb
(a.School of Public Policy and Administration;b．School of Humanities ＆ Social Science Xi'an Jiaotong University，Xi＇an 710049，China)

Age structure changes of workers participating in pension insurance system have a direct influence on the revenue and expenditure of social insurance fund．Adopting a feedback way of measuring population age structure to improve the population growth equation and based on the improved equation，this study builds a measuring model of age structure of workers participating in pension insurance．Then the paper makes an empirical study on the age structure of CPF(central provident fund)members in Suzhou industrial park．The outcome shows that age structure of CPF members develops leap－forward，the percentage of members over 60 years old will reach its peak to 47．3%in 2050，and the dependency ratio will decrease from 636∶1 to 1．13∶1 in 2050．

workers participating in pension insurance system;age structure;actuarial models

F840.61

A

1007—5097(2011)07—0150—05

10.3969/j.issn.1007－5097.2011.07.036

2010—01—05

国家社会科学基金项目“中国人口结构变动与社会保障需求研究”(07BRK004)

马 伟(1968—)，男，陕西西安人，讲师，博士研究生，研究方向:失业保险;

王立剑(1983—)，男，河北邯郸人，博士研究生，研究方向:社会保障统计与精算。

［责任编辑:余志虎］