基于主成分分析和贝叶斯正则化BP神经网络的GDP预测*
2011-12-19喻胜华
喻胜华,邓 娟
(1.湖南大学 经济与贸易学院,湖南 长沙 410079; 2.中南大学 数学科学与计算技术学院,湖南 长沙 410075)
基于主成分分析和贝叶斯正则化BP神经网络的GDP预测*
喻胜华1,邓 娟2
(1.湖南大学 经济与贸易学院,湖南 长沙 410079; 2.中南大学 数学科学与计算技术学院,湖南 长沙 410075)
选用财政收入、财政支出、消费品零售总额、实际利用外资、进出口总额以及全社会固定资产投资等对GDP有显著影响的6个因子,用1985~2008年中国的宏观经济数据建立了一个基于主成分分析和贝叶斯正则化BP神经网络的预测模型,并把它应用于我国GDP的预测。实证结果表明:通过主成分分析法和贝叶斯正则化方法对BP神经网络进行改进,可简化网络结构,增强泛化能力。与其它常用的预测方法相比,该方法数据输入简便,收敛速度快,拟合曲线光滑,且在预测精度上有明显的优势。
主成分分析;贝叶斯正则化;BP神经网络;预测
一 引 言
GDP(国内生产总值)是衡量国民经济发展情况最重要的一个指标,也是经济运行状况的综合反映。自1985年以来,GDP的核算已经成为我国经济管理部门了解经济运行状况的主要手段和制定经济发展战略、规划、年度计划以及各种宏观经济政策的主要依据。因此,如何采用科学的方法来预测GDP,已成为经济学界研究的主要课题。目前,预测GDP的方法很多,主要有回归预测法[1]、时间序列预测法[2-4]、灰色预测 法[5][6]、马 尔 可 夫 预 测 法[7]以 及 人 工 神 经 网 络 预 测法[8-12]等。前面四种方法属于传统的预测方法,它们大都是对变量之间的因果关系进行分析,实际应用中存在多重共线性和序列相关等问题,而且不可避免的丢失了信息,模拟效果不佳,预测精度难以令人满意。而人工神经网络是用来模拟人脑结构及智能特点的一个前沿研究领域,它可以通过网络学习达到其输出与期望输出相符的结果,具有很强的自适应、自学习和纠错能力。人工神经网络有多种模型,其中BP神经网络模型最成熟,其应用也最为广泛。但BP算法在本质上是属于一种非线性的优化方法,存在学习时收敛时间较长,易陷入局部极小点等缺点[10]。近年来,有学者把几种预测方法综合起来使用,得到了比单一预测更好的预测结果[13-15]。本文用主成分分析方法简化BP神经网络的输入单元数,用贝叶斯正则化算法提高网络的泛化能力,建立了主成分 贝叶斯正则化BP神经网络预测模型,并在此基础上对我国的GDP进行了为期三年的预测和分析。与此同时,还与几种常用的预测方法进行了比较研究,实证结果表明:本文建立的模型有较强的仿真与预测能力。
二 主成分—— 贝叶斯正则化BP神经网络
(一)主成分分析法

主成分分析法是从所研究的多个指标中,求出几个新指标,这些指标可以综合原有指标的信息,且彼此间不相关的统计分析方法。其原理为:设有p个指标X1,X2,…,Xp,作指标的线性组合
Z2,…,Zm的累计贡献率。累计贡献率越大,损失的数据信息就越少,通常取m使累计贡献率达到70%~80%以上。
(二)贝叶斯正则化BP神经网络
BP网络是一种采用误差反向传播算法的前馈网络,通常由输入层、隐含层和输出层构成,层与层之间的神经元采用全互连的连接方法,通过相应的网络权系数相连,每层内的神经元没有连接。权值不断调整的过程,就是网络的学习过程,此过程一直进行到网络的输出误差减少到可以接受的程度,或进行到预先设定的学习次数为止。
尽管BP网络具有很强的非线性映射能力,网络中间层各层的处理单元数及网络学习系数可根据具体情况任意设定并获得不同的性能,但BP算法是一种梯度下降法,算法性能依赖于初始条件,学习过程易陷于局部极小,且它的学习速度、精度和网络推广能力等都较差,不能满足应用的需要。所以,我们采用贝叶斯正则化的BP网络算法,一般算法以均方误差函数为目标函数,权值问题不能得到优化,而贝叶斯正则化在目标函数中增加权值这一项,并用贝叶斯方法自动调节参数,优化网络结构,从而提高网络的泛化能力。
贝叶斯正则化的BP网络算法的基本思想是[16][17]:
给定 一 组 训 练 样 本S= {(p1,t1),(p2,t2),…,(pm,tm)},神经网络学习的目的是寻找能有效逼近该组样本的函数f,使误差函数最小化,一般情况下,神经网络的训练误差函数采用均方误差函数:

为了提高泛化能力,可以在目标函数里加上网络权值平方的算术平均值,即目标函数变为:
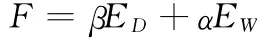
三 实证研究
在参考已有文献的基础上选取对GDP有显著影响的6个因子:财政收入(FR),财政支出(FE),消费品零售总额(TRG),实际利用外资(AUC),进出口总额(TIE),全社会固定资产投资(FA)(数据来源于1985—2008年《中国统计年鉴》)。不难看出:上述指标之间的相关性较大,信息重叠较多,不宜直接用BP网络建模,先采用主成分分析法消除指标间的重叠信息,获得主要的综合指标。
(一)主成分的提取
由原始数据可得到主成分的特征值及方差贡献率(如表1),主成分的贡献率表示该主成分反映原指标的信息量,累积贡献率表示相应几个主成分累积反映原指标的信息量。由表1可知,前两个主成分的贡献率分别为94.483%、5.199%,累积贡献率达到了99.683%,表明前两个主成分涵盖着所有指标99.683%的信息量,于是选取前两个主成分来进行分析。
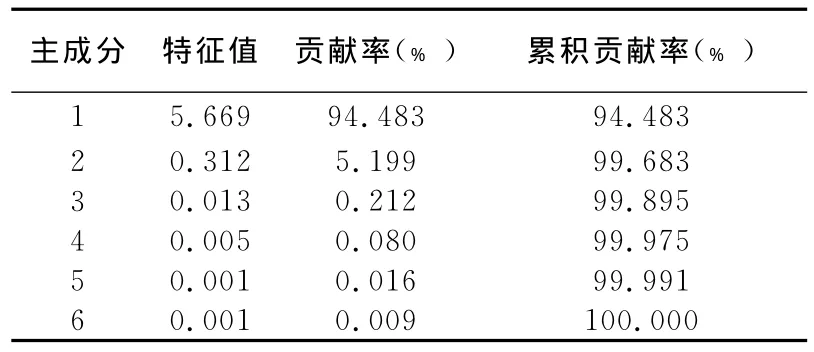
表1 各主成分的特征值及方差贡献率
(二)BP神经网络模型的确定
BP神经网络模型主要由输入层、隐含层、输出层以及各层之间的传输函数等组成。在设计网络结构时,一般先考虑一个隐层,当一个隐层的节点数很多仍不能改善网络性能时,才考虑再增加一个隐层。由于本文的样本容量少,所以只选取一个隐含层;输入层为2,即为主成分的个数;输出层为1,即为历年的GDP;隐含层和输出层的转移函数分别采用S型正切函数tansig和线性函数purelin。
隐含层的神经元数目选择是个十分复杂的问题,往往需要根据设计者的经验和多次实验来确定,因而不存在一个理想的解析式来表示。隐含层单元的数目与问题的要求、输入输出单元的数目都有着直接关系。若数目太少,则网络所能获取的用以解决问题的信息太少;若数目太多,不仅增加训练时间,而且误差不一定最小,也会导致容错性差、不能识别以前没有训练过的样本以及出现过度拟合等问题,因此,合理选择隐含层单元数非常重要。利用边界层确定隐含层单元数的方法可以得到本文数据网络隐含层单元数的范围是(6,11),采用1985年到2005年共21组数据进行BP网络训练,2006年到2008年共3组数据进行测试。发现当隐含层节点数为8时,各项预测误差最小,说明对这组数据而言,当输入节点为2,输出节点为1,隐含层节点为8时,网络具有较好的预测能力。
(三)贝叶斯正则化BP神经网络的训练、仿真与预测
选定BP神经网络的结构后,利用神经网络工具箱可得到如下的训练过程图:
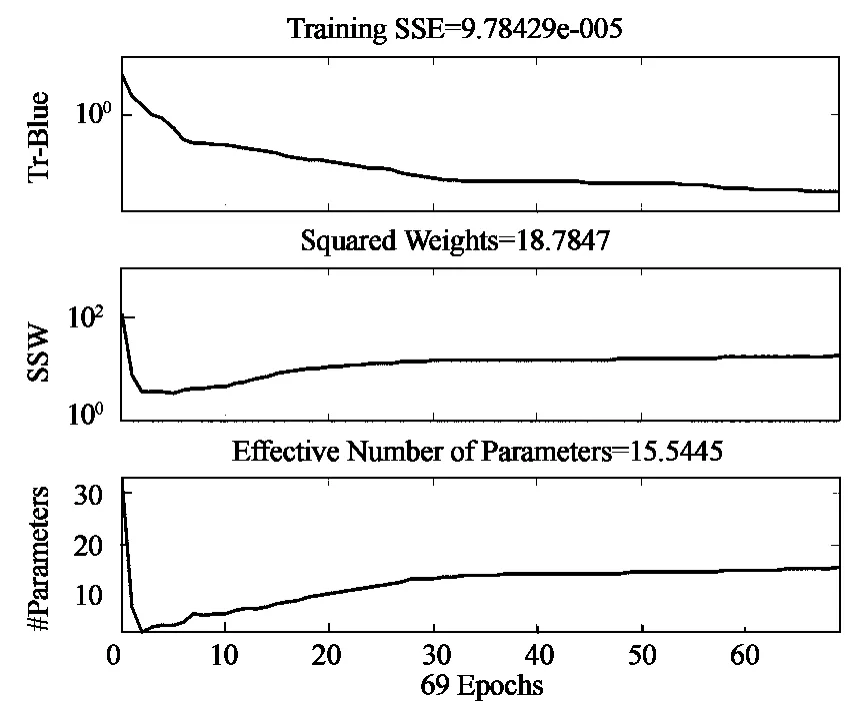
图1 神经网络训练过程图
从训练结果可以看出,网络经过69次就达到拟合精度9.78429e-005,有效参数个数为15.5,达到理想状态,从网络的误差图也可以看出,网络的收敛速度快,学习效率高。
下表是经过训练后的网络对于样本的仿真值,由表2可以看出:21组训练样本的最大相对误差为-1.88%,说明训练后的网络对于训练样本而言性能是优良的,这是BP网络共有的优点。通过适当调整参数,训练后的网络能对训练样本无限地接近。
用训练后的网络对测试数据进行预测(见表3):
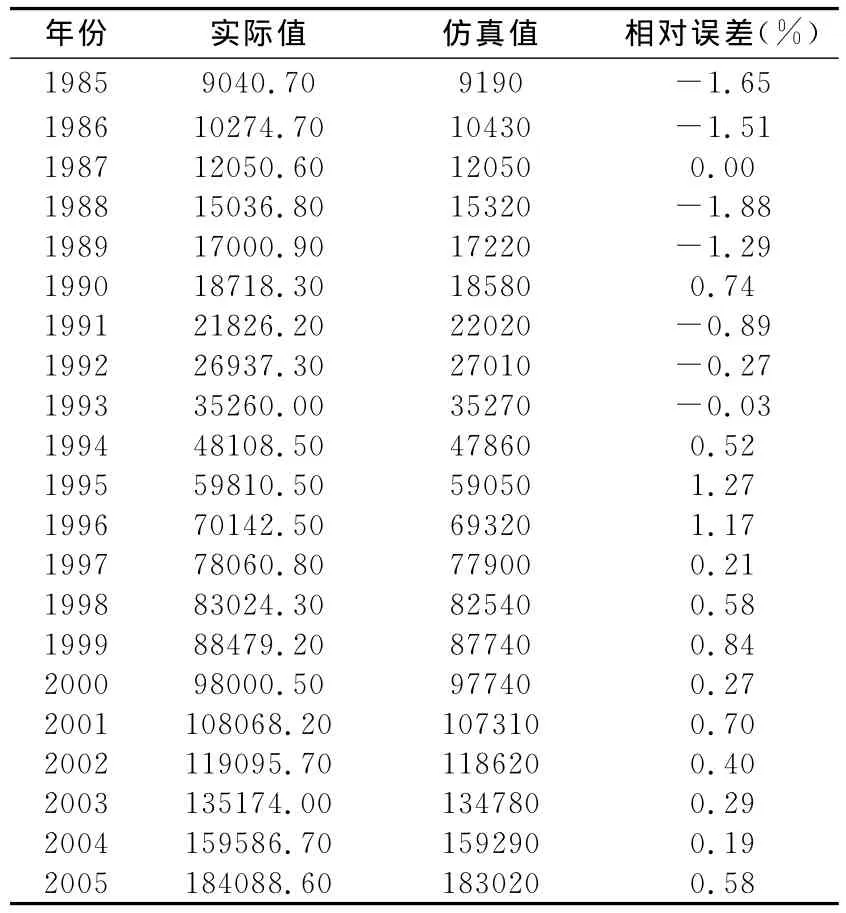
表2 模型训练后的仿真值与相对误差
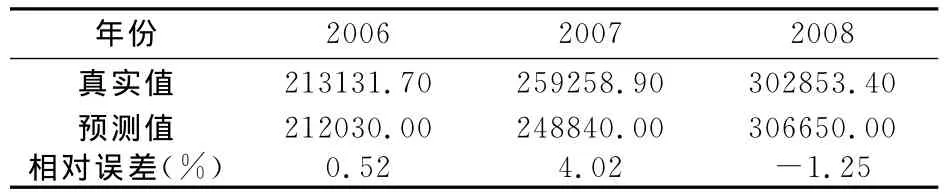
表3 模型预测值
由表2和表3可以看出:对前21组样本拟合的最大相对误差为-1.88%,对后3组样本预测的最大相对误差为4.02%,而最小相对误差仅为0.52%。一般来说,若误差在5%左右,则表明拟合效果与预测效果良好。
四 与其它预测方法的对比分析
为了进一步说明本文所用方法的预测效果,现将它与如下几种预测方法作对比分析。为简便起见,我们把本文所用的预测方法称为方法一。
方法二:不先提取主成分,而是直接使用原始数据作为网络输入。网络参数的设置同方法一,即精度为1e-4,最大迭代次数为10000,隐含层节点数选为8;
方法三:不用贝叶斯正则化算法,而改用一般的梯度下降法;
方法四:不用贝叶斯正则化算法,而改用LM算法;
方法五:ARIMA法;
方法六:多元回归法;
方法七:指数平滑法。
上述七种预测方法的预测结果及相对误差如下表:
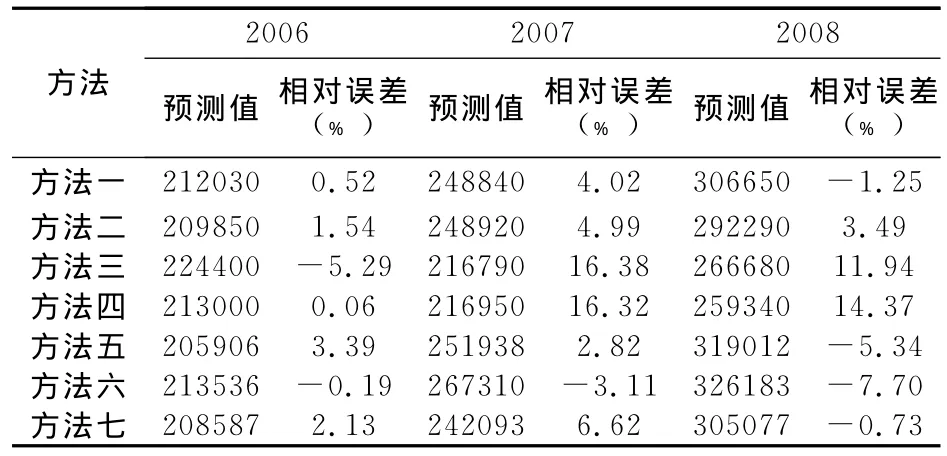
表4 与其它预测方法的比较分析
从表4可以看出,方法二的最大相对误差为4.99%,而最小相对误差也有1.54%,大于方法一的相对误差,可见预测效果要差一些,表明精简输入后的网络对样本信息有更好的概括,对测试数据有更好的预测能力。
通过训练样本发现:一般的梯度下降法,收敛缓慢,经过10000次训练,样本误差仍然不能达到期望的1e-4,在同等训练条件下,一般的梯度下降法训练精度不够,拟合曲线不光滑,对2007年我国GDP的预测,相对误差为16.38%,三年平均相对误差为11.2%,预测效果较差。
改进后的LM算法,收敛速度快,经过8次训练,就使网络误差达到了4.86824e-005,但LM算法的拟合曲线极不光滑,虽然对2006年的预测,相对误差仅为0.06%,但对于2007年,相对误差便上升到16.32%,三年平均相对误差也达到了10.25%,出现了过度拟合。存在过度拟合的网络虽然训练残差较小,但结构臃肿,并未得到足够的信息,这会导致对于许多未知数据的预测不起作用,泛化能力差,实际应用性差。
而使用贝叶斯正则化的BP网络,收敛速度快,仅经过69次训练就使网络误差达到了期望值,预测值中最大相对误差仅为4.02%,且拟合曲线光滑,贝叶斯正则化算法的预测效果明显优于一般的梯度下降法和LM算法。
标准BP算法收敛速度慢是限制其广泛应用的主要原因,LM算法收敛速度快,但容易导致过度拟合,预测效果不佳。
从表4也可以看出,ARIMA法、多元回归法以及指数平滑法的预测效果不及方法一。实际上,ARIMA预测方法应用的前提是假定事物的过去会同样延续到未来,但影响经济增长的因素非常复杂,它不仅受国家宏观经济政策的影响,而且也会受众多偶然的外部冲击和自然因素的影响。因此,依靠其历史数据建立起来的时间序列预测模型的预测精度必然受到影响。多元回归模型则对以往的数据要求比较高,模型的建立需要大样本且要求样本有较好的分布规律,预测的结果是由每一个影响因素决定的。因此,一旦影响经济增长的某一个因素发生了结构性的变化,依靠历史数据建立起来的回归预测模型的精度也必然受到影响。指数平滑模型是一种特殊的 ARIMA的模型,即IMA(1,1),因为ARIMA模型的拟合综合考虑了序列的趋势变化、周期变化及随机干扰,并借助模型参数的调整最终使拟合残差不再包含可供提取的非随机信息成分,成为白噪声或近似白噪声,所以,多数情况下,ARIMA方法的预测效果要优于传统的指数平滑法。
五、结 论
本文利用主成分分析和贝叶斯正则化BP神经网络方法对我国宏观经济数据进行了研究,BP网络的“黑箱”特性使得人们难以理解网络的学习和决策过程,不能明确获得内部权值所反映的学习信息,这对我们准确地把握经济现象的本质是个阻碍,本文使用了6个对经济增长影响较大的变量,通过主成分分析后简化为两个主成分,这两个主成分解释了所有变量99.683%的信息,再通过BP网络建立映射关系,得到相应年份的仿真与预测值,但无法知道是哪个或哪些变量对经济增长起怎样的作用,我们主要是利用这一模型对历史数据进行模拟,将目前并不清晰的信息体现在模型中,积累这些未知的知识,从而做出更为准确的预测。通过与几种常用的预测方法的对比分析发现:本文所用的方法数据输入简便,收敛速度快,拟合曲线光滑,泛化能力强,且在预测精度上有明显的优势。
[1] 胡艳国,武友新,江恭和.支持向量机在GDP回归预测中的应用研究[J].微计算机信息,2007,23(11):17-19.
[2] 华鹏,赵学民.ARIMA模型在广东省GDP预测中的应用[J].统计与决策,2010,(12):166-167.
[3] 许阳干.广西GDP的时间序列分析与预测模型[J].沿海企业与科技,2010,(7):54-57.
[4] 王春峰,宋袆.混沌时间序列分析法在生产总值预测中的应用分析[J].天津大学学报(社会科学版),2007,9(2):137-139.
[5] 穆昭光.灰色预测模型在江苏省GDP预测中的应用分析[J].现代商贸工业,2009,22:32-33.
[6] 户孝俊,马德山,贾田田.灰色GM(1,1)预测模型及其在甘肃省GDP预测中的应用[J].甘肃农业,2010,(5):25-26.
[7] 吴隽,陈长彬.东南亚各国人均GDP的马尔可夫法预测[J].番禺职业技术学院学报,2007,6(4):26-31.
[8] 张兴会,杜升之,陈增强,袁著祉,莫荣.主成分分析法在神经网络经济预测中的应用[J].数量经济技术经济研究,2002,(4):122-125.
[9] 欧邦才.基于BP神经网络的经济预测方法[J].南京工程学院学报(自然科学版),2004,2(2):11-14.
[10]陈志高.遗传算法和BP神经网络在GDP预测中的应用[J].计算机与数字工程,2009,37(9):172-175.
[11]赵秀恒,李明,李昆山.BP神经网络在GDP预测中的应用研究[J].河北经贸大学学报(综合版),2006,6(3):90-93.
[12]柯年前,张吉刚.基于主成分分析和BP网络的我国GDP预测。科技创业月刊,2008,(8):107-108.
[13]雍红月,包桂兰.组合时间序列ARMA模型在经济预测中的应用——内蒙古十一五期间GDP预测[J].数学的实践与认识,2008,38(21):19-23.
[14]王莎莎,陈安,苏静,李硕.组合预测模型在中国GDP预测中的应用[J].山东大学学报(理学版),2009,44(2):56-59.
[15]梁文光.广东省GDP时间序列预测——基于神经网络与ARIMA模型[J].技术和市场,2010,17(6):7-9.
[16]武妍,张立明.神经网络泛化能力与结构优化算法研究[J].计算机应用研究,2002,(6):21-25.
[17]王飞.基于贝叶斯向量自回归的区域经济预测模型:以青海为例[J].经济数学,2011,28(2):95-100.
GDP Prediction Based on Principal Component Analysis and Bayesian Regularization BP Neural Network
YU Sheng-hua1,DENG Juan2
(1.School of Economics and Trade,Hunan University,Changsha 410079,China;2.School of Mathematical Sciences and Computing Technology,Central South University,Changsha 410075,China)
We choose financial income,financial expenditure,total retail sales of consumer goods,actually used foreign investment,total import and export volume and social fixed assets investment,such as six factors,which have a significant effect on GDP.A forecasting model based on principal component analysis and Bayesian regularization BP neural network was established by using the Chinese macro-economic data in 1985~2008,and was applied to predict the GDP of China.The empirical results show that the principal component analysis and Bayesian regularization are utilized modify BP neural network,which can simplify network structure and strengthen generalization.Compared with other commonly used methods of forecasting,this method has simple data input,fast convergence rate,smooth fitting curve,and there is significant advantage in the prediction accuracy.
principal component analysis;Bayesian regularization;BP neural network;prediction.
P338.9
A
1008—1763(2011)06—0042—04
2010-11-16
喻胜华(1966—),男,湖南宁乡人,湖南大学经济与贸易学院教授,博士.研究方向:数量经济学.
