气流干燥过程的数学模拟及研究进展

郑晓冬

（滨州学院化学与化工系）

气流干燥过程的数学模拟及研究进展

郑晓冬*

（滨州学院化学与化工系）

气流干燥器是化工生产中广泛应用的干燥装置。由于气流干燥过程的复杂性，影响过程模拟的因素较多。介绍了气流干燥模拟的基本计算过程与方法，并展望了未来的研究方向及发展。

气流干燥器 数学模拟 干燥 动量 热量 质量

0 前言

气流干燥也称 “瞬间干燥”，是固体流态化的稀相输送技术在干燥方面的应用。该法是使加热介质 （空气、惰性气体、燃气或其他热气体）和待干燥固体颗粒直接接触，并使待干燥固体颗粒悬浮于流体中，因而两相接触面积大，强化了传热传质过程，广泛应用于散状物料的干燥单元操作[1]。

气流干燥过程是高能耗操作，包含多种物理化学现象，是热量、质量和动量交互影响的复杂传递过程，工业上实施常以经验为主，具有相当的盲目性。为了更好地掌握和分析这一复杂过程，在其开发、设计与控制等方面取得新进展，气流干燥过程的数学模型与模拟已受到广泛重视。

1 干燥过程模型化的一般方法

气流干燥过程模拟建立在表征干燥过程数学模型的基础上，通过计算机预测一定操作条件下的物料行为，并完成实物实验难以进行的考察，从而确定最适宜的操作模式与条件。Reay[2]将干燥过程模型分为三种：以经验为基础的放大因子模型，以实验模拟为基础的输入/产出模型和以理论分析为基础的基本模型。后者比前两者更可靠，其适用范围不受以往经验的限制，可以外推。建立基本模型必须具有物料和干燥器的基础资料，即要建立物料模型和设备模型，它们有如下关系，由图1表示。

干燥过程基本模型是以干燥物料表面与干燥介质间同时发生的动量、热量和质量传递及干燥物料内部的传递为研究对象，具体模型化内容可用图2表示[3]。

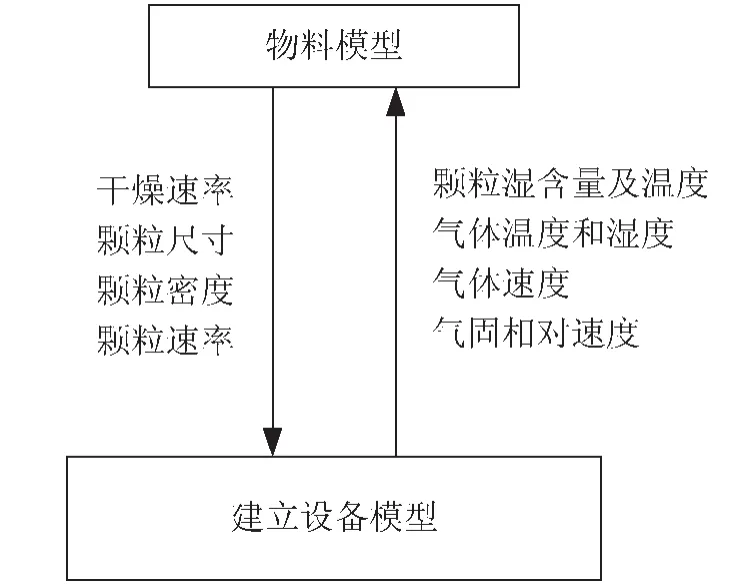
图1 干燥过程基本模型

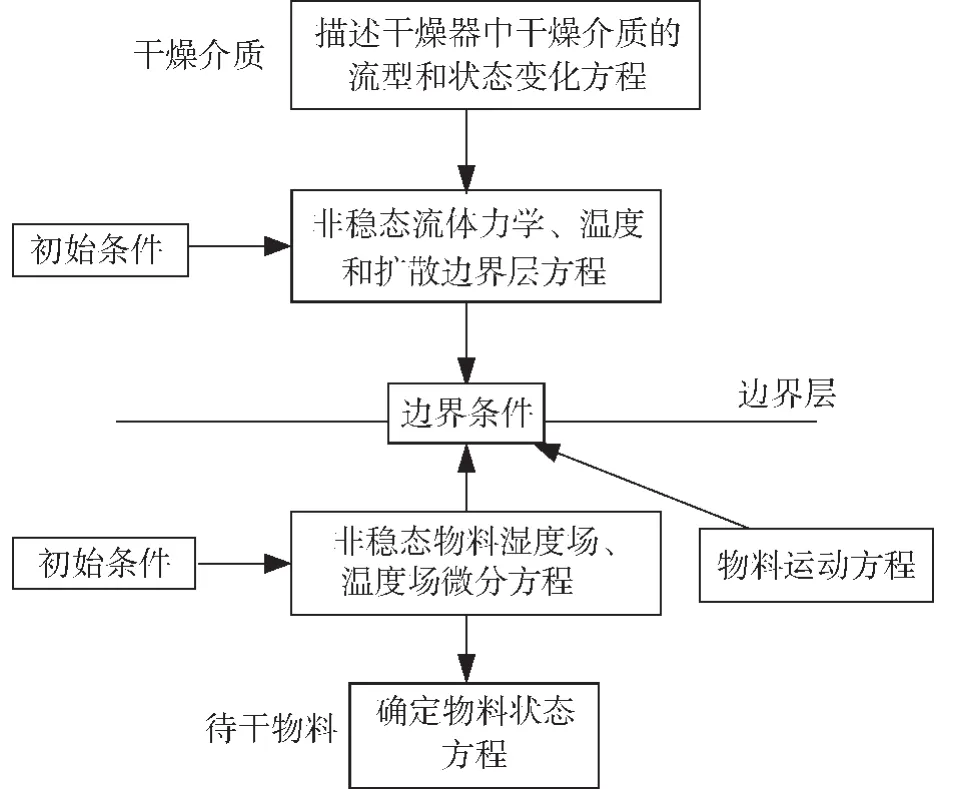
图2 传递通用模型

由于实际过程的复杂性，建模时须根据过程的实质作必要的简化与假设，以便于模型求解。简化与假定的有效性需由实验验证。如对易干燥的多孔物料可忽略内部扩散等。

1.1 物料模型

干燥过程的物料模型就是用数学表达式描述物料的干燥特性。物料模型的主要功用除计算任意颗粒湿含量、温度及任意气体温度、湿度及气固相对速率下的干燥速率外，还可提供颗粒大小、密度和比热随湿含量与温度变化的关系。

完整的物料模型应该包括下列内容：一定温度、湿度和气速条件下，少量物料的多个间歇干燥曲线；根据以上数据，预测任意操作条件下的干燥速率；预测一定温度和湿度下，吸湿性物料的平衡湿含量数据；计算颗粒尺寸、密度和比热随湿含量降低产生的变化。

1.2 设备模型

设备模型就是用数学表达式描述干燥器的流体力学、传热传质、压头损失、能量消耗等性能，它要求物料模型提供有关干燥速率和颗粒特性的基础数据。若建立设备模型所需的参数无法用理论计算得到，通常可由中间实验、现场测定或数据外推获得。

设备模型应包括下列几项内容：流体流动特性，如气体速度分布与压降；颗粒运动规律；热量质量传递规律及与设备设计变量有关的诸多关系式，如物料在干燥器中的停留时间、曳力系数、摩擦系数、质热传递系数等。这些内容彼此关联而不可分，建立设备模型时，必须综合考虑这些交互影响的作用。

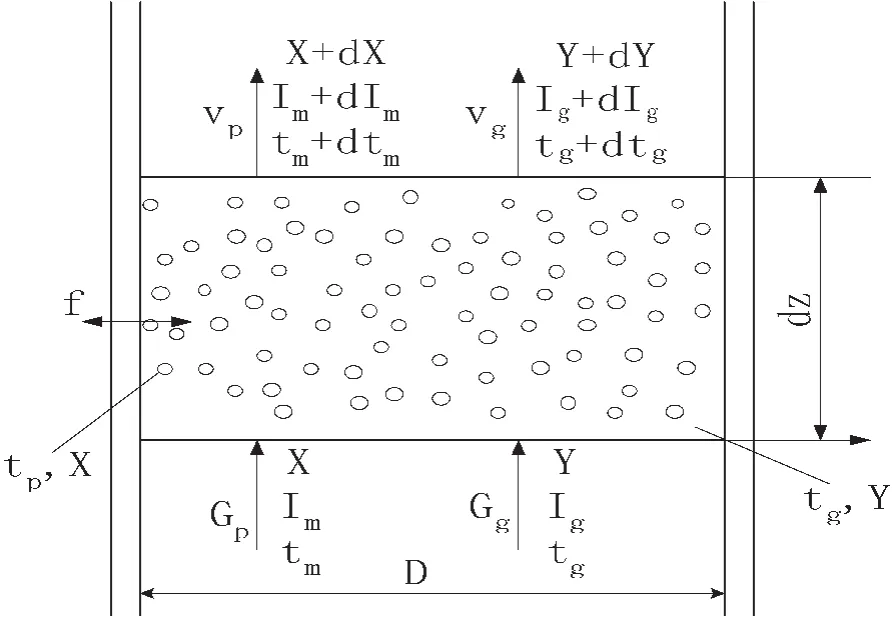
图3 干燥管的体积元

2 气流干燥模拟的基本计算过程及方法

2.1 模型基本假设

物料颗粒是圆球形，干燥中由于失去湿分而引起的粒径、密度变化可忽略不计；物料颗粒均匀分散悬浮于气流干燥管中， 颗粒浓度对其运动轨迹的影响可忽略，对任意体积元有如下结构示意图[4]（见图3）。图中，vg为气体速度，vp为湿物料颗粒的速度；X为物料的湿含量，Y为空气的绝对湿度，Im为含1 kg绝干物料的湿料中的焓值，Ig为含1 kg绝干气的湿料中的焓值；tm为物料温度，tg为气体温度；Gp为绝干物料的质量流率，Gg为绝干空气的质量流率。

2.2 模型中的基本方程

对于气流干燥模拟数学模型而言，主要数学方程应包括以下几个方面[5]：

（1）物料、热衡算模型；

（2）传递过程及气－固间传热量模型；

（3）气－固粒一维运动模型；

（4）针对不同类型干燥管的其它有关模型；

（5）相关优化目标函数模型。

2.3 模型的基本计算方法

气流干燥模拟的基本计算方法是将干燥管分段，根据入口条件，利用气流干燥模型逐段进行计算，并以每段的出口条件作为下一段的入口条件，再重复进行计算，直到计算完整个管长。主要采用以下两种方法。

（1）半湿含量降低法[6]

20世纪70年代学者Nonhebel得出了一种气流干燥模拟方法，他的基本出发点是按照降水幅度划分单元，即在每个单元内，物料含水率降低至所需降水幅度的一半。其主要步骤为：

a）将干燥管按降水幅度分段，每一段中假设物料水分降低一半；

b）入口处物料和介质的参数是已知的；

c）假设第一段出口处的物料温度；

d）利用热平衡和质平衡原理，求解第一段出口的风温和热风湿含量；

e）计算平均温差；

f）按传热原理计算干燥时间θh；

g）按传质原理计算干燥时间θm；

h）比较θh和θm，看其是否相等。如果不等，则利用逐步逼近的方法修正参数，直至 θh=θm为止；

i）以第一单元输出参数作为第二单元的输入参数，重复计算，并依此类推，一直到物料含湿量达到了要求的终水分为止；

j）将各段的时间相加即可得到总的干燥时间，干燥时间乘以物料平均速度即为干燥管的总长。

（2）长度单元法

长度单元法是目前气流干燥模拟中常用的一种方法。它是沿干燥管长划分小单元，在小单元内，根据热质平衡原理建立各状态参数随管长变化的微分方程组，并用数值解法对其求解，得出每个单元出口处的各个状态参数，重复计算第二个单元、第三个单元……，直到计算完整个管长为止。

3 气流干燥过程模拟的发展

气流干燥是一个比较复杂的传热传质过程，是动量、热量、质量相互影响、相互耦合的结果。在以往设计计算中， 通常采用传热速率法及试算法。前者将有关设计参数及干燥介质物性在整个干燥器中平均化[7]，这样得到的结果与实际情况偏差很大；后者以逐点试算和数值积分进行计算， 虽然能比较清楚地反映气流干燥过程基本原理[8-9]， 但计算过于繁复。绝大多数模型都是假设颗粒的性质均匀并且不随干燥过程的进展而发生粒径的收缩，只考虑在稳定条件下的一维流动干燥过程。这一类模型有Thorpe、Wint和Coggan在1973年建立的模型，Matsumoto和Pei以及Martin和Saleh在 1984年建立的模型，Saastamoinen在1992年建立的模型等[10]。

从近年来的文献可以看出，气流干燥的数学模型正处于迅速发展之中，目前模型的确定仍然是气流干燥研究中的一个热点。

Adewumi（1990）[11]针对垂直的气流干燥装置，提出了一个二维流动的数学模型，并讨论了轴向速度的影响。

Fyhr和Rasmuson[12]利用过热蒸汽作为加热介质，分别对不同粒径分布的物料进行实验研究，并给出了一个较为复杂的气流干燥半理论模型。

Levy和Borde[13]以湿PVC颗粒为研究对象，利用传热传质基本原理，建立了完整的流动数学模型，在模型中考虑了颗粒在干燥时发生收缩的情况。

Pelegrina和Grapiste[14]在前人的基础上，对谷物的气流干燥作了进一步探讨，并在以下几方面取得了进展。

（1）在颗粒相动量方程中，考虑了管壁和颗粒间的摩擦力，摩擦因子f的形式为Yang[15]给出的计算公式：

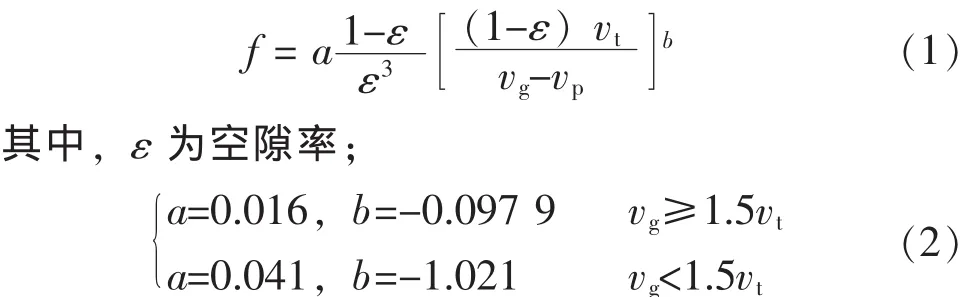
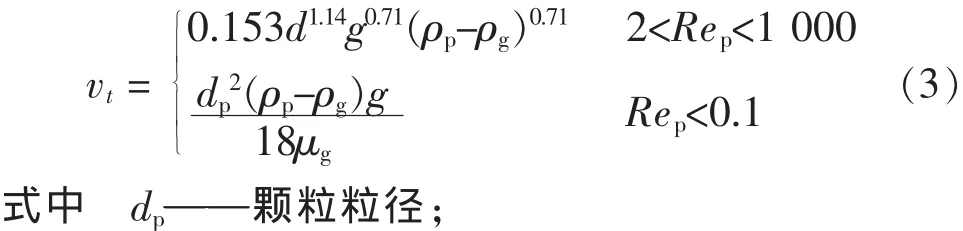
g——重力加速度；

ρg——湿空气的密度；

ρp——湿物料的真密度；

μg——湿气体的黏度。

（2）在模型中加入了两个形状因子，并考虑了不同颗粒形状采用不同传质、传热系数。

（3）给出了气体速度的微分方程式。

在国内也有不少人作过这方面的工作，郑国生[16]等根据两相流的基本理论，对球形颗粒物料建立了直管式气流干燥数学模型。在颗粒动量方程中，气固相阻力采用的是Arostoopour和Gidaspow[17]提出的针对球形颗粒群的表达式：

在模型中还考虑了颗粒空隙率的影响，并系统地建立了空气、水、水蒸气特性参数方程。整个模型没有较难确定的参数，计算简单，易于求解。经实验验证，其计算结果与实验数据吻合。

4 结论

气流干燥器虽然结构简单，但其中进行的干燥过程却很复杂。干燥过程同被干燥物质的特性有非常密切的关系。用于不同物料的、不同类型的干燥器其数学模型也不同。不同数学方程、相关参数的选取，以及假设的不同，对模拟结果也会有较大的差别。因此数学模型在应用之前必须要经过试验数据的验证。

由于影响因素的复杂性，目前模型主要建立在一维流动的数学模拟的基础上。二维流动数学模型应是今后研究的主要发展方向。

[1] 化学工程编辑委员会.化学工程手册[M].北京：化学工业出版社，1989.

[2] Reay D.Modelling continuous convection dryers for particulate solids-progress and problems [J].Drying，1985，85：67-74.

[3] Houska K.Computer-aided design of dryers[J].Advance in Drying，1987（4）.

[4] 曾伍兰.脉冲式气流干燥过程的实验与模拟研究[D].青岛：青岛科技大学，2004.

[5] 张言文.气流干燥器数学模型及分段设计计算方法[J].计算机与应用化学，2006，23（4）：381-384.

[6] Matsumoto S.A mathematical analysis of pneumatic drying of grains[J].Journal of Heat and Mass Transfer，1984（6）：851-855.

[7]Keey R B，Suzuki M.Theoretical foundations of drying technology[J].Advance in the Drying，1980（11）：1-22.

[8] Kemp I C，Bahu R E.A new algorithm for dryer selection[J].Drying Technology，1995，13：1 563-1 578.

[9]Fortes M， Okos M R.Drying theories：Their bases and limitations as applied to food and grain [J].Advances in drying，1980（12）：119-154.

[10]Pelegrina A H，Crapiste G H.Modelling the pneumatic drying of food particles [J].Journal of Food Engineering，2001，48：301-310.

[11]Adewumi M A，Arastoopour H.Pseudo-two-dimensional steady-state two-phase flow model for gas-solids vertical pneumatic conveying systems [J].International Journal of Engineering Fluid Mechanics，1990，3（11）：53-70.

[12]Fyhr C，Tasmuson A.Mathematical model of a pneumatic conveying dryer[J].AIChE Journal，1997，43 （1）：2 889-2 902.

[13]Levy A，Borde I.Steady state one-dimensional flow model for a pneumatic dryer[J].Chemical Engineering and Processing，2001，38：121-130.

[14]Pelegrina A S，Crapiste G H.Modelling the pneumatic drying of food particles [J].Journal of Food Engineering，2001，48：301-310.

[15]Yang W C.A correlation for solid friction factor in vertical pneumatic conveying lines[J].AIChE Journal，2004，50（3）：548-551.

[16]郑国生，曹崇文.颗粒物料气流干燥的数学模型[J].北京农业工程大学学报，1994，14（2）：35-32.

[17]李长友.小麦干燥机理研究 [J].农业工程学报，1993，9（1）：83-91.

Mathematics Simulation and Research Progress on Pneumatic Drying Process

Zheng Xiaodong

The pneumatic dryer is the extensive applying apparatus in chemical production.Because of the complexity in drying process，many factors contribute to the process simulation.This paper introduced the primary calculating process and methods of pneumatic drying simulation，and predicted the research direction and development in the future.

Pneumatic dryer； Mathematics simulation； Drying； Momentum； Heat； Quality

TQ 028

*郑晓冬，男，1980年生，硕士，助教。滨州市，256600。

2011-05-01）