蛛形图的全图和中心图的均匀染色＊

赵金丽， 卜月华

(浙江师范大学数理与信息工程学院，浙江金华 321004)

用V(G)和E(G)分别表示图G的顶点集和边集．称映射φ:V(G)→{1，2，…，k}为图G的一个正常k-染色，如果φ使得V(G)中任何2个相邻的顶点u，v，φ(u)≠φ(v);称χ(G)为最小的颜色数k，使得图G 有正常 k-染色［1］．如果 G 的顶点集合可以剖分成 k 个独立集 V1，V2，…，Vk，使得||Vi|-|Vj||≤1(i≠j)成立，则称图G是k-均匀可染的，(V1，V2，…，Vk)称为一个均匀独立集剖分．使得图G均匀k-可染的最小的整数 k 为图 G 的均匀色数，记为 χEq(G)［2］．显然，χEq(G)≥χ(G)．

给定一个图G=(V，E)，对图G每一条边分割1次，即在每条边上插入一个顶点，连接所有在G中不相邻的顶点．对图G进行这样的操作后所得到的图称为G的中心图，记为C(G)．

给定一个图G，定义图G的全图T(G)如下:T(G)的顶点集合为V(G)∪E(G)，T(G)中满足下面条件之一的2个顶点x，y相邻:

1)x，y∈V(G)以及 x，y在 G 中相邻;

2)x，y∈E(G)以及 x，y在 G 中相邻;

3)x∈V(G)，y∈E(G)，x，y在 G 中关联．

一个图G称为是一个蛛形图［3］，若G是一棵树且至多存在一个度数大于2的顶点v，顶点v称为头点．蛛形图有时也称为广义星图．

对于一些特殊图的全图和中心图的均匀染色，Ali Akbar等［4］撰文进行了讨论，得到了如下结果:

定理1［4］路Pn的全图的均匀色数 χEq［T(Pn)］=3．

定理 2［4］对于圈 Cn，若 n≡0(mod 3)，则 χEq［T(Cn)］=3．

而当n不能被3整除时，其均匀色数的情况仍不清楚．

定理 3［4］星图 K1，n的中心图的均匀色数 χEq［C(K1，n)］=n．

定理 4［4］等完全二部图 Kn，n(n≥3)的中心图的均匀色数 χEq［C(Kn，n)］=n．

定理5［4］完全图Kn(n≥4)的中心图的均匀色数 χEq［C(Kn)］=3．

有关均匀染色的其他结果可参考文献［5］．

本文讨论了蛛形图的全图和中心图的均匀染色问题，得到了蛛形图的全图的均匀色数(定理6)和蛛形图的中心图的均匀色数(定理7)．

定理6 设G是一个蛛形图，删去头点后共有n(n≥3)条路，该n条路记为Pi(1≤i≤n)，且|Pi|=n-1，则 χEq［T(G)］=n+1．

证明 设蛛形图G的头点为v，删去v后，把该n条路分别记为Pi=vi1vi2…vin(1≤i≤n)，eij表示Pi中连接 vi(j-1)和 vij(1≤i≤n，2≤j≤n)的边，连接 v 与 vi1的边记为 ei1(1≤i≤n)．NT(G)(vij)表示点 vij在T(G)中的邻域．

根据全图的定义，有:

因 T(G)是包含由 v，e11，e21，…，en1的 n+1 个顶点所构成的完全子图，故 χEq［T(G)］≥χ［T(G)］≥n+1．另一方面，若能够证明顶点集合V［T(G)］可以划分成n+1个独立集，且任意2个独立集之间的元素个数至多相差1，则有 χEq(［T(G)］)≤n+1．

为了证明方便，分n≤6和n≥7两种情况来证明．当n≤6时，具体给出每个独立集的元素，从而证明 χEq(［T(G)］)=n+1．

1)n≤6．

①n=3．令:T1={e11，v21，v23，v31，v33};T2={e21，v13，e12，e32，v22};T3={v11，e13，e22，v32，e31};T4={v，v12，e23，e33}．Ti(i=1，2，3，4)是元素个数分别为 5，5，5，4 的独立集，此独立集剖分满足条件“任意独立集之间的元素个数至多相差1”．

②n=4．令:T1={v13，e11，v21，v31，e33，v41};T2={v23，e21，e14，e34，v42，e44};T3={v33，e31，e12，v24，e22，v44，e42};T4={v11，e13，v22，e24，e32，v43，e41};T5={v，v12，e23，v32，e43，v14，v34}．Ti(i=1，2，3，4，5)是元素个数分别为6，6，7，7，7的独立集，此独立集剖分满足条件“任意独立集之间的元素个数至多相差1”．

③n=5．令:T1={e11，v21，v31，e33，v41，v51，e53，v44};T2={v24，e21，e14，e34，v42，e44，v52，e54};T3={e31，v13，e15，v23，v43，v53，e55，v11};T4={e41，v15，e12，v25，e22，v35，e32，v55，e52};T5={v54，e51，e13，v22，e24，v33，e35，v45，e42};T6={v，v14，e23，e43，v12，v32，v34，e25，e45}．Ti(i=1，2，3，4，5，6)是元素个数分别为 8，8，8，9，9，9 的独立集，此独立集剖分满足条件“任意独立集之间的元素个数至多相差1”．

④n=6．同理成立(略)．

2)n≥7．令:Vij={vij，ei(j+2)}，1≤j≤n-2;Vi(n-1)={vi(n-1)，ei1};Vin={vin，ei2}．其中 1≤i≤n．每个Vij(1≤i，j≤n)的元素个数都为2，共有n2个集合，每个集合在T(G)中都是独立集，现在用这些集合继续构造n个独立集．令:

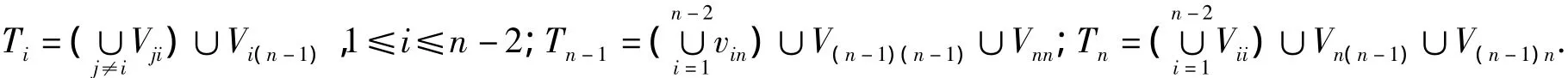
至此，上述n2个集合Vij(1≤i，j≤n)合并为n个独立集，每个独立集的元素个数均为2n，则还剩下头点v没包括进去，从T1到Tn-1中分别选取2个不与头点v相邻的、且彼此也都不相邻的顶点，共同构成Tn+1．此时分2种情况:

①n为奇数．在每个Ti(1≤i≤n-2)中选取2个顶点，取法如下:

当i是奇数时，在Ti中选取顶点e2(i+2)，e(n-1)(i+2);当i是偶数时，在 Ti中选取顶点v1i，v(n-2)i．然后再在Tn-1中选取顶点v1n，v(n-2)n．所选取的2(n-1)个顶点互不相邻．令:

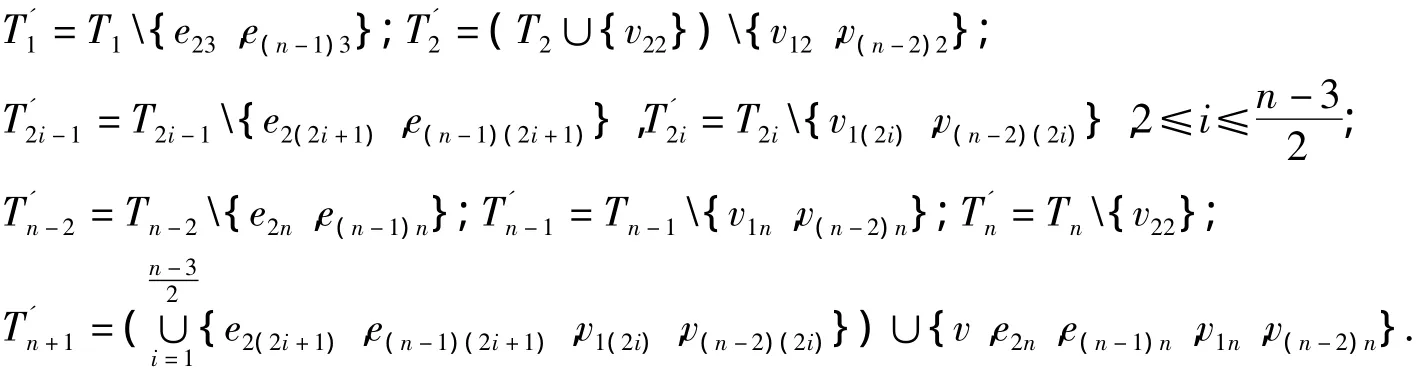
②n为偶数．在每个Ti(1≤i≤n-2)中选取2个顶点，取法如下:

当i是奇数时，在Ti中选取顶点e2(i+2)，e(n-1)(i+2);当i是偶数时，在Ti中选取顶点v1i，v(n-2)i．然后再在Tn-1中选取顶点e32，e42．所选取的2(n-1)个顶点互不相邻．令:

定理7 设G是一个蛛形图，删去头点后共有n(n≥3)条路，该n条路记为Pi(1≤i≤n)，且|Pi|=

证明 记v为蛛形图G的头点，删去v后，把该n条路分别记为Pi=vi1vi2… vin，1≤i≤n，在C(G)中，vi(j-1)与 vij之间插入的顶点记为 uij(1≤i≤n，1≤j≤n)．其中:vi0=v;NC(G)(vij)表示点 vij在 C(G)中的邻域．根据中心图的定义，有:

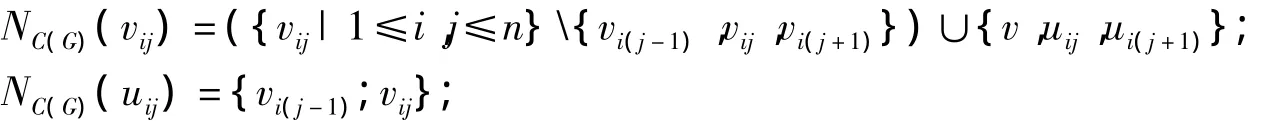
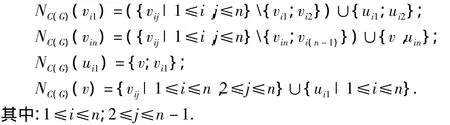
因为原图中不相邻的顶点在中心图C(G)中相邻，所以C(G)中的每个独立集至多含V(G)中的2个顶点，且只能是在G中相邻的2个顶点．下面根据n的不同情况进行讨论．

此时，有|Vi1|=3(2≤i≤n)，|Vi((n+1)/2)|=3(1≤i≤n)，|V11|=4，|Vij|=4(1≤i≤n，2≤j≤(n-1)/2)满足均匀染色的条件，所以当n=2k+1时，χEq［C(G)］=(k+1)n=(k+1)×(2k+1)=2k2+3k+1．定理7证毕．

关于确定图的全图和中心图的均匀色数的文献还非常少，可以继续研究的问题依然很多，如:

问题1 在定理6和定理7中的蛛形图删去头点后路长为l(l≠n-1)的情况下，其全图和中心图的均匀色数为多少?

问题2 其他结构稍复杂的图类，如二叉树等，其全图和中心图的均匀色数为多少?

［1］卜月华．图论及其应用［M］．南京:东南大学出版社，2000:198-199．

［2］Zhu Junlei，Bu Yuehua．Equitable list coloring of planar graphs without short cycles［J］．Theoretical Comput Sci，2008，407(1/2/3):21-28．

［3］Marek Kubale．Graph Colorings［M］．Rhode Island:American Mathematical Society，2004:139-144．

［4］Ali Akbara M M，Kaliraja K，Vernold Vivinb J．On Equitable Coloring of Central Graphs and Total Graphs［J］．Electronic Notes in Discrete Mathematics，2009，33(1):1-6．

［5］朱俊蕾，卜月华．图 Pn∨Km，n的均匀全色数［J］．浙江师范大学学报:自然科学版，2007，30(1):58-64．