黄冈职院“十二·五”时期招生规模灰色预测

周振祥，刘喜咏

(黄冈职业技术学院，湖北，黄冈，438002)

黄冈职院“十二·五”时期招生规模灰色预测

周振祥，刘喜咏

(黄冈职业技术学院，湖北，黄冈，438002)

以黄冈职业技术学院为个案，以历年招生人数为原始资料，采用灰色系统GM(1，1)模型，通过建立不同维数数列模型和等维不同时期数列模型，选择最佳预测方案，对“十二·五”时期招生规模进行了可靠预测。

招生规模;灰色预测;发展趋势

黄冈职业技术学院于1999年7月，经教育部批准，在原三所中专学校的基础上组建成立。1999年——2003年，是学校组建之后建设发展初期，也是全国、全省高职教育快速发展的大好时机，1999年当年招收高职专科生800人，2003年招生3，925人，年均增长30%;2004年——2005年，高职教育招生规模进一步扩大，全省2003年高职招生7.46万人，2004年、2005年分别达到8.87万人和10.4万人，较2003年，年均增长29%，其中，黄冈职业技术学院同期招生年均增长45.5%。2006年，湖北省印发了《省人民政府关于大力发展职业技术教育的决定》，明确了“十一·五”期间湖北省职业技术教育发展目标和任务，高职教育不再是扩大规模，而是突出高职教育内涵建设。教育部、财政部开始共同组织实施国家示范性高等职业院校建设计划，标志着全国高职教育由规模扩张向突出内涵建设转变。黄冈职业技术学院2006年——2010年招生规模呈良性发展态势，这一时期招生规模年均增长13%，这对提高黄冈职业技术学院办学效益，促进学院内涵建设，确保招生规模稳步增长，取到了重要的调控作用。

据多项研究提示，“十二·五”时期，各级基础教育学校生源呈显著下降趋势，高职教育生源将会受到直接影响。“十二·五”时期及其以后，高职教育招生规模到底将如何估计?这将是各高职院校、各级地方政府关注的焦点问题。本文以黄冈职业技术学院为例，采用灰色系统GM(1，1)模型 对“十二.五”时期招生规模进行了科学预测。

1 灰色预测模型概述

一般来说，基于灰色GM(1，1)模型的预测，都称为灰色预测，也即对一灰色系统的预测。灰色系统也称信息不完全系统，其中一部分信息是已知的，另一部分信息是未知的，系统内各因素间具有不确定关系。如历年招生规模数，就是各时期影响招生规模的已知信息、未知信息、系统内各因素间综合作用的结果，各因素间的作用关系一般是不能白化的，所以说它是一个灰色系统。招生规模作为一灰色系统，其行为总是要受到许多确定和不确定因素的影响，每个因素本身又有子因素，子因素又含有子因素……。任何一个灰色系统，因为影响行为的因素太多，不可能给出实用的预测模型。但系统的每一个行为数据，都是影响系统行为的所有因素作用的总结果，即任一时刻的行为数据(白化值)，都是系统所有因素的总映射值。如果按系统行为数据 X(k)，k=1，2，…n 构造 GM(1，1)模型进行预测，则预测模型形式上是非因素的，而实质上却是全因素的，不过这种全因素是在灰色意义下才成立，这就是灰色预测的立论基础，即白化值都是系统全部因素影响的总结果。

因此在灰色系统建模中，视系统的原始数据列(白化值)都是一定时期诸多因素综合作用的结果，其中存在诸多确定和不确定的灰色作用量。不同时期灰色作用量是有差异的，它将影响到模型的预测精度。因此本例在建立预测模型过程中，分别不同维数(年度数)建立模型，分析其不同维数的预测精度，结合定性分析，指定较合适的模型作为预测模型。

本例在确定其最佳维数模型的基础上，考虑到不同时期数据列灰色作用量的差异，又采用等维依次递变的方式，建立GM(1，1)模型，分析不同时期模型的预测精度，结合定性分析，指定最佳的预测模型用于实际预测。

2 灰色系统GM(1，1)建模 (2)

设招生规模原始数据列为X(0)

设X(0)= ［x(0)(1)，x(0)(2)，…，x(0)(n)］，作一次累加生成，得到

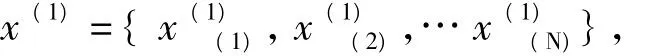
构造累加矩阵B与常数项向量YN，即

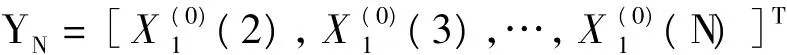
GM(1，1)预测模型的灰色微分动态模型

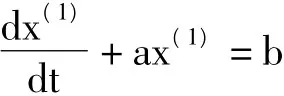
其中a，b分别称之为发展系数和灰色作用量，a的有效区间是(-2，2)。应用最小二乘法求解灰参数

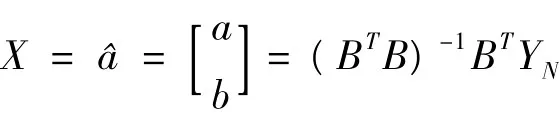
将灰参数代入时间响应函数：

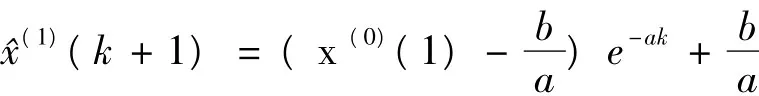
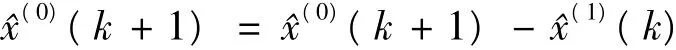
3 预测模型精度检验

为保证所建灰色预测模型有较高的精度应用于预测实践，需要对预测结果进行精度检验。

3.1 误差检验：

求出x(0)(k)与^x(0)(k)之残差e(k)、相对误差△k和平均相对误差

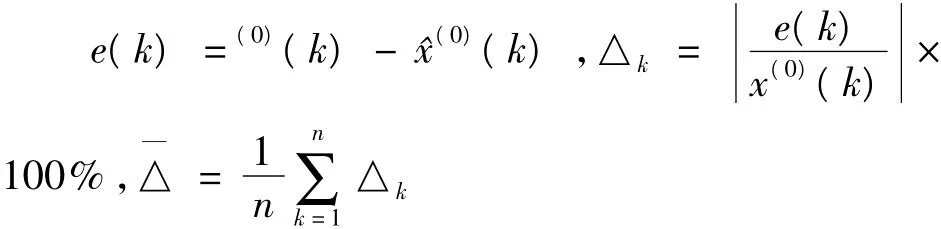
3.2 后验差检验(2)：

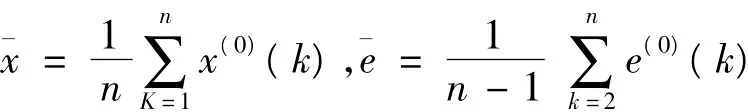
求出原始数据方差s12：

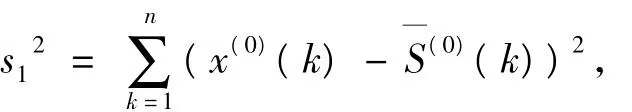
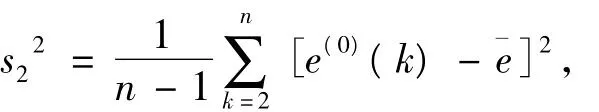
再计算后验比C和小误差概率P：

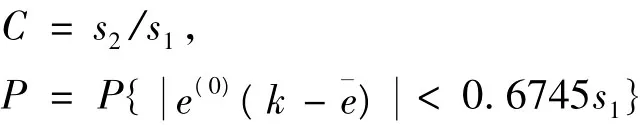
通常e(k)、△k、C值越小，P值越大，则模型精度越好。若C ＜0.35，P ＞ 0.95，则模型精度为一级。

4 “十二·五”招生规模预测与验证分析

4.1 建立原始数据列

取黄冈职业技术学院历年高职招生人数原始数据资料(3)，建立x(0)(k)原始数列(如表1)。

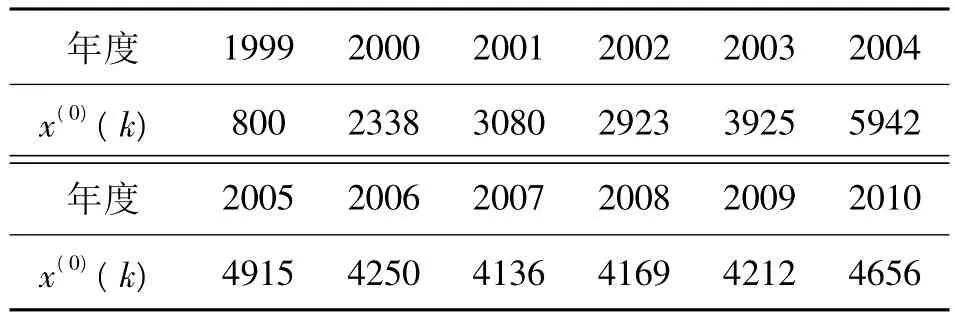
表1 黄冈职业技术学院历年高职招生人数原始数据序列

4.2 灰色模型检验性预测

4.2.1 不同维数模型检验性预测。取 1999——2008年原始数列依次递减建立10维、9维、8维、7维、6维、5维、4维模型，2009、2010年原始数据作为模型精度检验值，用以计算模型误差检验。结果如表2。

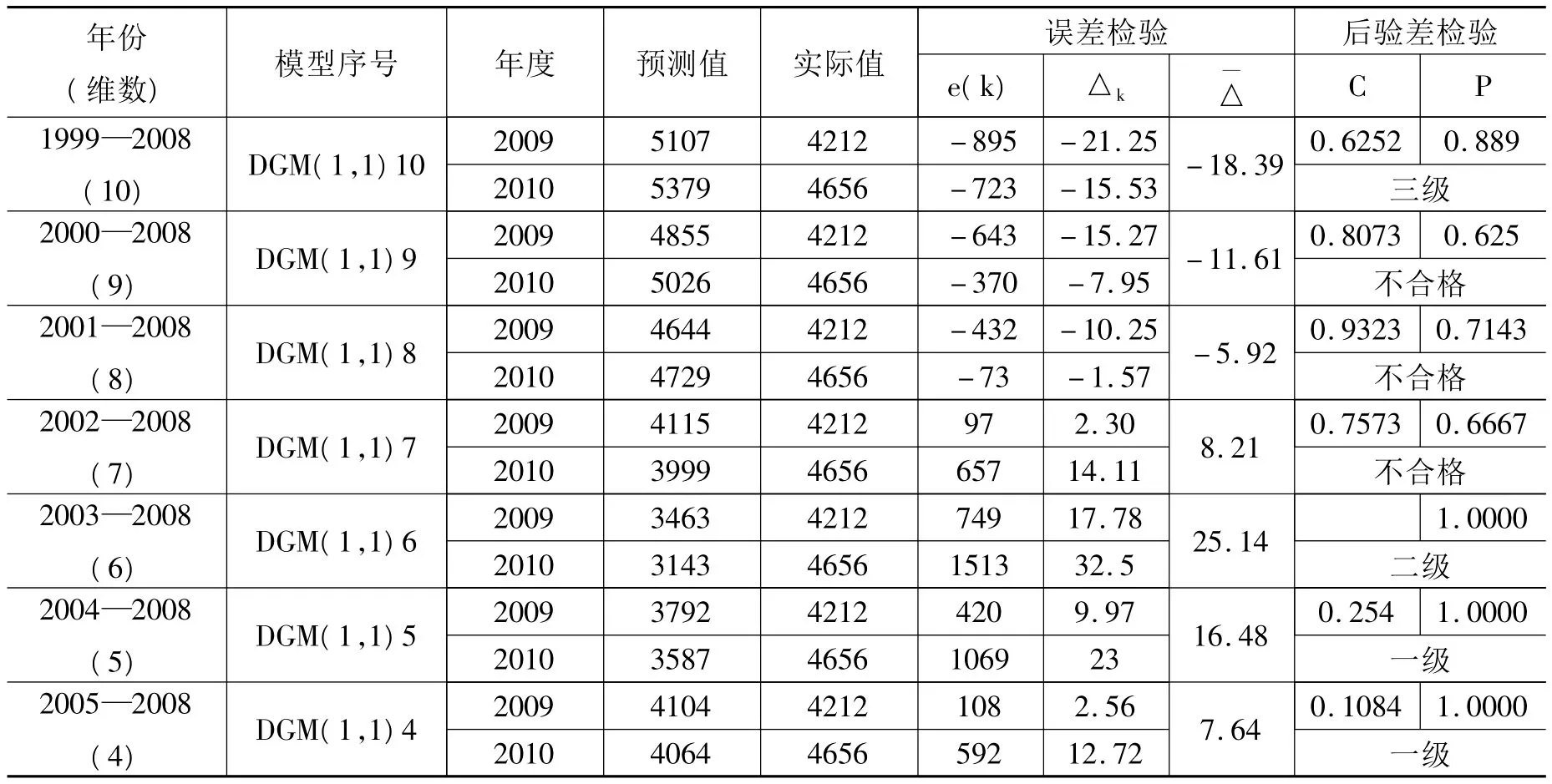
表2 不同维数模型精度检验

据表2分析，不同维数预测，呈现维数越高，相对误差越大的趋势。越是远离现在时刻，相对误差也越大。灰色预测模型要求不仅相对误差要小，且后验差检验要达到一级精度，预测结果才可信可靠。综合比较，2005—2008年，4维预测模型平均相对误差小，后验差检验，模型精度最高，故本例指定DGM(1，1)4为预测模型。

4.2.2 不同时期模型检验性预测

取2000—2010年原始数据列，采用等维依次递变的方式建立不同时期等维数列模型。以模型预测值^x(0)(k+1)、^x(0)(k+2)与相对应年份实际值x(0)(k)作为误差检验的参照值。结果如表3。

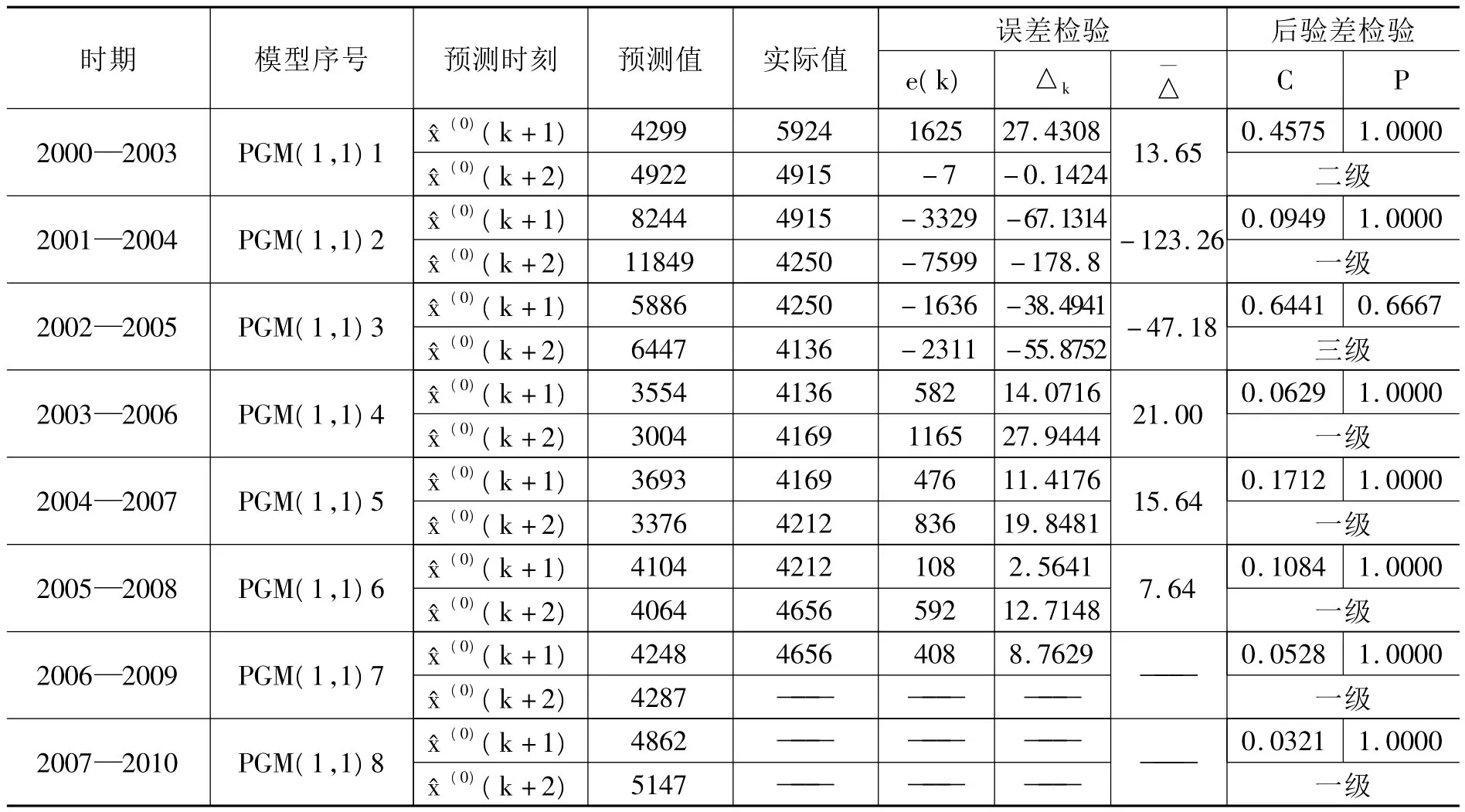
表3 不同时期等维模型精度检验

据表3分析，同是4维数列模型，但不同时期数列，灰色作用量的差异，导致误差也是不同的。并有越是远离现在时刻的原始数列，相对误差越大，平均相对误差由远至近，有依次递减趋势。说明不同时期数据列及远离现在时刻的数据列存在的灰色不确定因素对预测有干扰。本例采用4维数列模型，原始数据列包含的年份长度较短，有效的降低了时间数列中的灰色不确定因素的影响，从而4维GM(1，1)模型，后验差检验大部分模型精度都比较高。据此分析，本例PGM(1，1)8模型后验差检验精度最高，误差检验呈持续走低趋势，反映该模型运行机制是稳定的，持续有益的。故本例指定PGM(1，1)8模型为实际预测模型。

4.2.3 黄冈职业技术学院“十二·五”招生规模预测

经以上分析，本文选取PGM(1，1)8模型为实际预测模型，预测结果如表4。

表4 黄冈职业技术学院“十二·五”招生规模数灰色预测

2011年预测值为5262人，其中含新增高职医药类专业招生数。作为预测，都只是对未来发展趋势的一种估计，不可能十分的准确。但研究者又都希望预测值更能逼近真实，能对实际工作取到更准确的参考作用，故本例对预测值采用95%的置信区间进行估计，即黄冈职业技术学院2011年全日制高职专科生招生人数应在4999—5539之间。2012—2015年的预测值，可以看作是当年招生规模的中值，为提高其预测值的可信程度，需要采用等维递补预测，对各年度预测模型及时进行修正，到“十二·五”末，年招生规模有望突破6000人。

5 黄冈职院“十二·五”招生规模发展趋势分析

5.1 “十二·五”期间总体呈现平稳递增趋势

本研究结果，表明了未来五年内招生规模呈平稳递增趋势，这与湖北省教育事业发展主要指标［见《湖北省中长期教育改革与发展规划纲要(2011——2020)》］中提出的2015年，高等职业教育在校生68万(2009年58.39万)2020年达到73万，是相一致的。即今后五年内，生源基数会减少，但高职类总体招生规模不会减少。

5.2 “十二·五”期间，黄冈职院招生规模将会呈现稳中有升的发展态势

“十二·五”期间，我省必将继续突出、深化高职教育内涵建设，总体招生规模是稳中有升，但各高职院校能否保有现有的招生规模，依靠的不是招生计划，而是各具鲜明的办学特色。作为国家骨干示范院校建设单位的黄冈职业技术学院，重点是要抓住国家骨干示范校建设的契机，突出国家骨干示范院校建设内涵，巩固已有的办学成果，在“十二·五”期间，招生规模将仍然会呈现出稳中有升的发展趋势。

［1］邓聚龙.灰色系统基本方法［M］.华中理工大学出版社，1987(11).

［2］唐启义.DPS数据处理系统［M］.科学出版社，2010(2).

［3］黄冈职业技术学院辉煌60年.黄冈职业技术学院校庆文献.2010.

Grey Forecast of Enrollment Scale During“Twelve·Five-Year”Period of Huanggang Polytechnic College

ZHOU Zhen-xiang，LIU Xi-yong
(Huanggang Polytechnic College，Huanggang 438002 Hubei)

Taking Huanggang Polytechnical College as a case，with the enrollment number over the years as the original data，using the grey system GM(1，1)model，through the establishment of different dimensions and other dimension seriesmodel at different times，the author chose the best scenario，made a reliable prediction to the enrollment scale in“12.5”period.

Enrollment scale;Grey forecast;Developing trends

O141.4

A

1672-1047(2011)04-0092-04

10.3969/j.issn.1672-1047.2011.04.23

2011-07-05

周振祥，男，湖北武穴人，副教授。研究方向：高职教育。

［责任编辑：张克新］