超图圈偶边着色

朱俊杰

(昌吉学院数学系 新疆 昌吉 831100)

超图圈偶边着色

朱俊杰

(昌吉学院数学系 新疆 昌吉 831100)

本文根据N.Alon给出的一定范围内的圈偶边着色定义及色数定义，将其向超图上推广，得到了超图的最大偶边着色数。

圈偶边着色;超图

1 基本概念

1983年B.Devadas Acharya在［1］中首先提出了图圈偶边着色的概念，这一概念来源于对平衡标号图的研究，B.Devadas Acharya同时给出了图最大圈偶边着色的色数，一年后N.Alon给出了一定范围内最小圈偶边着色的等价定义及色数，本部分将图圈偶边着色的的概念推广到超图中，并得出了超图最大圈偶边着色的若干性质。

定义1［2］令X=(x1，x2，…，xn)是一个有限集，关于X上的一个超图H=(E1，E2，…，En)是X上一个有限子集簇，使得①Ei≠φ(i=1，2，…，m);②∪mi=1Ei=X。一个超图H=(E1，E2，…，En)若还满足③Ei=Ej⇒i=j则称H为简单超图。

定义2［3］超图的圈偶边着色，设H=(V，E)是一个顶点数为n分支数为k的有限无环的无向超图，设P={Ei}是E(H)的一个划分，使其满足:对于H中的每一个圈Z，至少存在一个Ei∈P使得

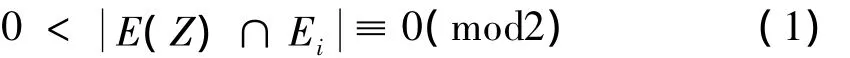
定义3［2］设v是超图H中一个顶点，v被称为H的一个割点如果H－v的连通分支数增加。H的所有部分超图中，不存在割点的部分超图称为H的块。

由定义可知，H中圈的集合是它中块的圈集合之并。于是有下列性质:

性质1 H是超图，εmin(H)=maxB∈ΒHεmin(B)，其中ΒH是H中块的集合。

性质2 H是超图，εmax(H)，其中ΒH是H中块的集合。

2 主要结果及证明

首先，我们给出France Dacar在1998年证明的结论。然后应用该结论分别推导出连通简单超图及多个连通分支简单超图最大圈偶边着色数的上界为和。最后在此基础上得到一致连通无圈和单圈超图最大圈偶着色的色数为别为和。

引理1［4］设H是n个顶点p个连通分支的超图，边集为{E1，E2，…，Em}，则H不包含圈当且仅当

由定理1可得如下两个推论。

推论1如果H是n个顶点k个连通分支的简单r－一致超图，那么

在图中有结论:任何n个顶点k个连通分支的图G，εmax(H)=n－k。那么我们自然猜想在r－一致超图H上是否有εmax(H)

定理2 H是n个顶点k个连通分支边集为(E1，E2，…，Em)的r－一致超图。若H不包含圈，则

证:若H不包含圈，则显然有εmax(H)=m。又因为H是r－一致超图，由引理m(r－1)=n－k，所以

定理3 H是n个顶点r－一致的连通超图。若H只包含一个圈，则

证:H包含一个圈不妨设为(x1，E1，x2，E2···，xp，Ep)，现去掉圈上的一条边E1，形成超图H'，即H'是(Ej|j∈{2，3，4，···，p})对H诱导的部分超图。H'仍是r－一致超图且不包含圈。设H'的顶点数是n'，连通分支数是t，则n'=n－s(s是E1中一度点的个数)。由定理2因为E1中除x1，x2以外的非一度点最多包含在H'的一个连通分支中，且E1中的x1，x2一定包含在H'的一个连通分支中，所以t≤r－s－1。又因为E1中除x1，x2的任一非一度点x必包含在H'的一个连通分支中且这个连通分支不包含E1中的其他点，否则假设一个连通分支P∈H'还包含E1的另一个点，则在P中存在一条x到的链(x，E1'，···，Eq')，这条链与E1在H中形成一个圈，与H只包含一个圈矛盾!所以t=r－s－1即t+s=r－1。因此。由于H'不包含圈，则显然有εmax(H')=m(H')(这里用m(H')表示H'的边数)，那么－1=m(H')，而m(H)=m(H')+1=

3.结束语

本文最终得到了一致的连通无圈和单圈超图最大圈偶着色的准确色数，应用同样方法也能对最小圈偶着色的色数进行估计，这样做使超图的圈结构更加清楚，同时也提供了研究超图圈的一种方法。当然，以上结论并没有得到一般超图圈偶着色的准确色数，这将有待进一步研究。

［1］B.Devadas Acharya.Even Edge Colorings of a Graph［J］.Journal of Combi－natorial Theory，series B 35(1983)78－79.

［2］C.Berge.Hypergraphs:Combinatorics of Finite Sets［M］.North Holland:Amst－erdam，1973.

［3］N.Alon.Even Edge Colorings of a Graph［J］.Journal of Combinatorial Theory，series B 38(1985)93－94.

［4］France Dacar.The cyclicity of a hypergraph［J］.Discrete Mathematics，182(1998)，53－67.

［5］Sundar Vishwanathan.On 2－coloring k－uniform hypergraphs［J］.Journal of Combinatorial Theory，series A 101 (2003)168－172.

O186

A

1671－6469(2011)05－0094－03

2011－09－12

昌吉学院研究生科研启动基金(2010SSQD022)

朱俊杰(1982－)，男，新疆阿克苏人，昌吉学院数学系，讲师，研究方向:离散数学。

(责任编辑:马海燕)