基于SPSS的煤质发热量相关因素分析及其回归模型研究＊

梅晓仁 陈 鹏 高永胜

(1.湛江师范学院商学院,广东省湛江市,524048;2.辽宁工程技术大学资源与环境工程学院,辽宁省阜新市,123000;3.神华集团有限责任公司安全监察局,北京市东城区,100011)

基于SPSS的煤质发热量相关因素分析及其回归模型研究＊

梅晓仁1陈 鹏2高永胜3

(1.湛江师范学院商学院,广东省湛江市,524048;2.辽宁工程技术大学资源与环境工程学院,辽宁省阜新市,123000;3.神华集团有限责任公司安全监察局,北京市东城区,100011)

使用SPSS统计软件的探索分析和相关分析功能,对某露天煤矿7#煤层的煤质数据进行了统计分析,得出该煤层中干基灰分和可应用基低位发热量两个煤质指标具有很强的负线性相关关系,并使用SPSS统计软件的线性回归功能建立了这两个指标的回归模型。结果表明,该回归模型可以对7#煤层的应用基低位发热量进行预测。

煤发热量 相关分析 回归模型 SPSS统计软件

煤的发热量不仅是评价煤炭质量的一项重要指标,而且是评价动力用煤的一项重要经济参数。动力用煤以发热量计价能较准确地反映煤炭的使用价值。但是,由于对测定发热量的环境条件和操作人员的专业水平要求较高,测试仪器的维护难度也较大,因此,发热量的测定一般都由专人负责。同时,测定发热量需要的时间较长,测定结果滞后,制约了煤炭企业在生产过程中对发热量的监控,给煤炭企业带来了不必要的损失。

由于形成煤的原始物质和沉积环境不同,因而煤的性质和成分也各不相同。由于发热量与水分、灰分等指标存在相关关系,因此,本文探究用回归模型计算发热量指标,并使用SPSS统计分析软件对发热量的相关因素进行相关分析和回归模型研究,以求提供一种简便、实用的测定方法。

1 SPSS软件及使用的统计方法简介

1.1 SPSS软件特点及功能

SPSS是Statistical Product and Service Solu-tions的缩写,即统计产品与服务解决方案,是世界著名的统计分析软件之一。它广泛用于经济学、生物学、心理学、教育学、医疗卫生、体育、农业、林业、商业和金融等各个领域。

1.2 相关性分析方法

在实际问题中,变量之间往往有着密切的关系,但又不能由一个或几个变量的值确定另一个变量的值,即当自变量x取某一值时,因变量y的值可能会有多个。这种变量之间的非一一对应的、不确定性的关系,称之为相关关系。SPSS通过绘制散点图和计算相关系数,来有效揭示事物之间相关关系的强弱程度。

在散点图上,如果两个变量之间的关系近似地表现为一条直线,则称为线性相关。如果一个变量x变化,导致另一个变量y明显变化,称之为强相关。如果两个变量之间的关系近似地表现为一条曲线,则称之为非线性相关。如果两个变量的数据点分布很分散,无任何规律,则称两个变量之间不相关。

相关系数以数值的方式精确地反映了变量之间线性关系的强弱程度。一般地,相关系数的取值在-1～+1之间。R>0,表示两变量之间存在正线性相关关系;R<0,表示两变量之间存在负线性相关关系;R=1,表示两变量是完全正相关关系;R=-1,表示两变量是完全负相关关系;R=0,两变量不存在线性相关关系;|R|>0.8,表示两变量之间具有较强的线性相关关系;|R|<0.3,表示两变量之间线性相关关系较弱。

1.3 回归分析方法

回归分析是研究一个或者几个变量的变动对另一个变量的变动的影响程度的方法,根据已知的资料或数据,找出它们之间的关系表达式,用已知的自变量的值去推测因变量的值或范围。线性回归的统计学原理如下:

假定对一组变量x1,x2,…,xp,y作了n次观测,得到观测值为:

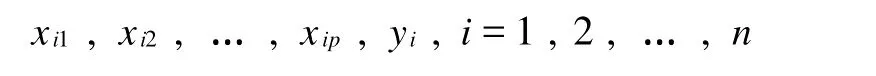
线性回归的一般数学模型是:

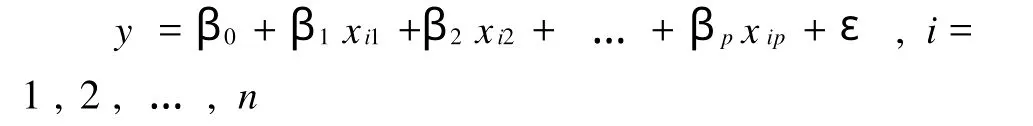
当已知一组自变量和因变量的值后,使用SPSS提供的线性回归分析方法就可以计算回归方程的回归系数和方差分析表中的参数等。

2 使用SPSS软件对煤质各指标进行相关性研究

2.1 数据的准备

选取山西省某大型露天煤矿的7#煤层的煤质数据作为研究对象。选取的指标包括钻孔号、煤样厚度、分析基水分、干基灰分、可燃基挥发分、干基全硫、氢含量、可燃基高位发热量和应用基低位发热量等9个指标,共94条数据。“-1.00”代表缺失值,如表1所示。

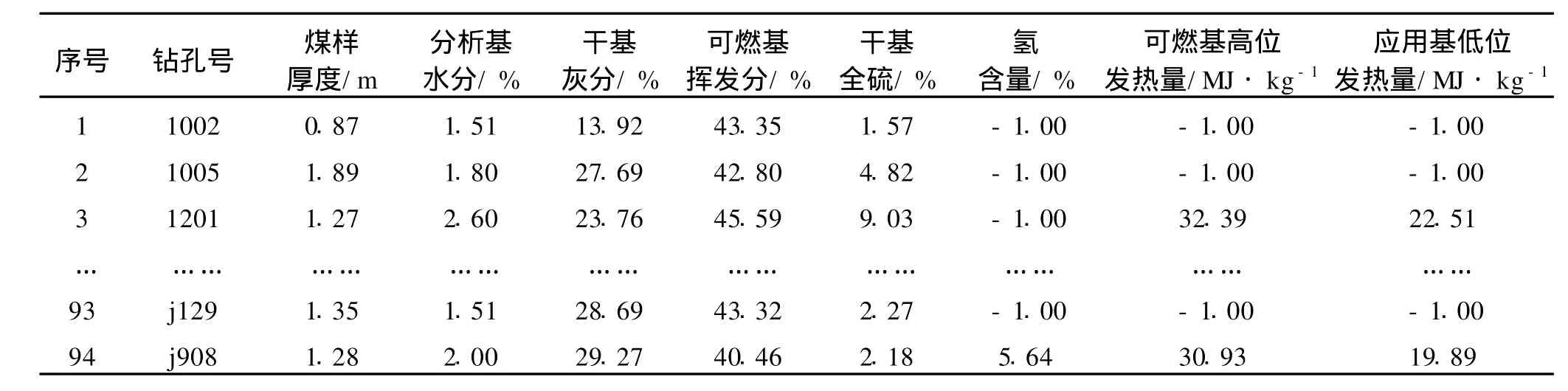
表1 7#煤层的煤质数据统计表

2.2 在SPSS中录入数据

启动SPSS后,单击SPSS左下方的“Variable View”标签,进入变量定义视图。定义的变量如图1所示。在“M issing”列中输入“-1.00”表示缺失值,分析统计时,SPSS自动忽略该值。

单击“Data View”标签,便可在数据编辑视图中输入数据。可以将单个的数据一一录入到SPSS中,也可以使用SPSS提供的导入功能,将已有的数据文件导入SPSS中,如果是Excel文件,则可以直接将Excel中的数据拷贝到SPSS中。

2.3 数据的探索分析

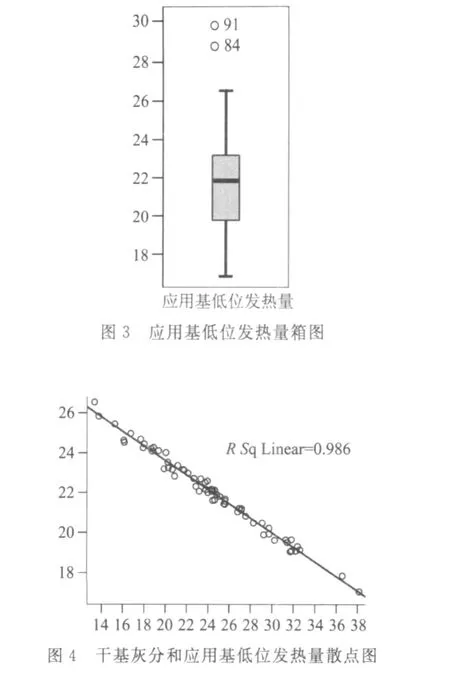
使用SPSS提供的探索分析,能够检查数据中的奇异值和极端值。SPSS提供了茎叶图(Stem-and-Leaf Plots)、箱图(Boxp lots)、正态分布检验Q-Q概率图、分层图(Sp read vs level p lot)等方法对数据进行探索分析。本文使用“箱图(Boxp lots)”对应用基低位发热量指标进行分析,其它指标分析的方法和过程与此相似。

依次单击菜单“Analyze”→“Descriptive Statistics”→“Exp lore”,打开“Explore(探索分析)”对话框,将应用基低位发热量选择到“Dependent List”,其它选项使用默认值,如图2所示。单击“OK”按钮,计算结果见图3。从图3中可以看出,应用基低位发热量有2个奇异值(图中用“○”表示):第84组和第91组数据,必须将其剔除,如果箱图中出现“★”,则表示该记录是极端值,也必须剔除。同样,对其它各项指标也进行探索分析。这个过程可能要重复几次。最后得到80组数据进行相关性分析和回归分析。

2.4 对煤质各指标进行相关性分析

2.4.1 绘制散点图

本文仅给出绘制干基灰分和应用基低位发热量两个指标散点图的方法和过程。依次单击菜单“Graphs”→“Scatter/Dot”,打开“Scatter/Dot”对话框,选择简单散点图(Simp le Scatter),点击“Define”按钮,打开“Simp le Scatterp lot”对话框,将应用基低位发热量选择到Y A xis(Y轴),将干基灰分选择到X Axis(X轴),其它选项使用默认值,单击“OK”按钮,绘制的散点图如图4所示。可以看出,干基灰分和应用基低位发热量具有很强的负线性相关关系,相关系数的平方值为0.986。

2.4.2 使用“二元相关分析”分析煤质各指标的相关性

依次单击菜单“Analyze”→“Correlate”→“Bivariate”,打开“Bivariate Correlations”对话框,限于篇幅,本文仅选取分析基水分、干基灰分、应用基低位发热量3个指标来计算相关系数,将这些指标选择到“Variables”中,其它选项使用默认值。单击“OK”按钮,计算这些指标之间的相关系数,计算结果见表2。由表2可以看出,在显著性水平0.01下,应用基低位发热量与其它指标显著相关(表中用＊＊标示)。其中,应用基低位发热量与干基灰分具有很强的负相关关系,相关系数为-0.993。因此,可以建立应用基低位发热量与其它指标之间的回归模型。

3 使用SPSS软件对煤质各指标回归模型进行研究

依次单击菜单“Analyze”→“Regression”→“Linear...”,打开“Linear Regression”对话框,将应用基低位发热量选择到“Dependent(因变量)”中,将分析基水分、干基灰分选择到“Independent(s)(自变量)”中,在“Method”中选择向前筛选策略“Forward”,其它选项使用默认值。单击“OK”按钮,得到模型综述结果、方差分析表(见表3)和模型系数表(见表4)。模型综述结果显示,回归过程只选择了与因变量具有最高线性相关系数的干基灰分作为自变量,而自变量分析基水分没有通过回归方程的检验,不能进入回归方程,因此,本例只得到了一个回归模型,即回归模型1,其相关系数R=0.995,说明因变量应用基低位发热量与自变量干基灰分相关性很强;拟合优度¯R2=0.989,说明自变量可以解释因变量98.9%的变异性;从表3中可以看出,F统计量的显著性概率Sig..=0.000,小于置信度0.05,说明因变量和自变量的线性关系是显著的,可建立线性回归方程;从表4中可以看出,回归模型的常数项为30.536,自变量的回归系数为-0.352,t统计量的显著性概率Sig.=0.000,小于置信度0.05,同样说明因变量和自变量的线性关系是显著的。因此,得到回归模型:

应用基低位发热量=30.536-0.352×干基灰分。

因此,使用该回归模型可以对应用基低位发热量进行预测。

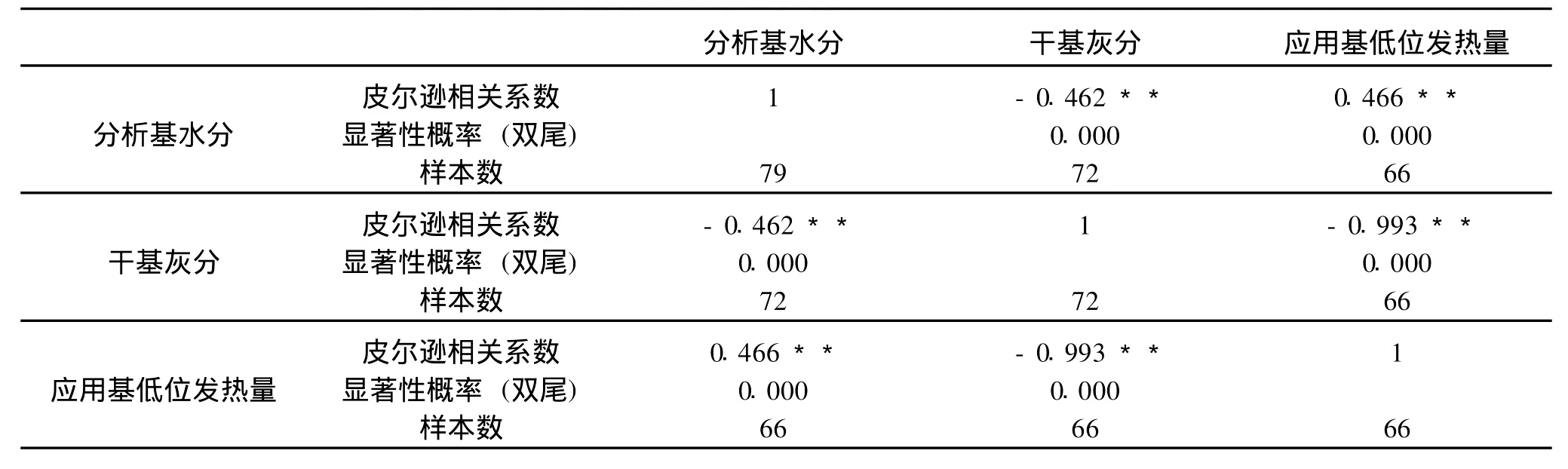
表2 煤质各指标的相关系数表

表3 方差分析表

表4 模型系数表

4 结语

本文以某露天煤矿的7#煤层的煤质数据作为研究对象,详细介绍了SPSS软件在煤质指标数据处理、相关性分析和回归分析中的使用方法和过程,为广大矿山地质工作者处理大量复杂数据提供一种简便易行的方法。

[1] 唐云杰.浅析煤的发热量与灰分的对应关系[J].中国煤炭,2004(11)

[2] 刘治青.煤中灰分与发热量相关性和回归方程[J].山西焦煤科技,2006(4)

[3] 陈洪博,白向飞,罗陨飞.煤的发热量与水分、灰分的关系研究[J].煤质技术,2010(4)

[4] 冯桂东.用回归方法研究煤的灰分、水分与发热量的关系[J].江苏煤炭,2001(1)

[5] 谭荣波,梅晓仁.SPSS统计分析实用教程[M].北京:科学出版社,2007

[6] 薛薇.SPSS统计分析方法及应用[M].北京:电子工业出版社,2004

[7] 高祥宝,董寒青.数据分析与SPSS应用[M].北京:清华大学出版社,2007

Correlative factors analysis and regression model research on coal calorific value using SPSS software

Mei Xiaoren1,Chen Peng2,Gao Yongsheng3
(1.Business School,Zhanjiang Normal University,Zhanjiang,Guangdong 524048,China;2.College of Resource and Environment Engineering,Liaoning Technical University,Fuxin,Liaoning 123000,China;3.Safety Supervision Bureau,Shenhua Group Corporation Limited,Dongcheng,Beijing 100011,China)

The coal quality data of No.7 coal mine of one open pit mine were analyzed using the Exp lore and Correlation Analysis functions of SPSS.It was concluded that the coal quality data of the dry ash and the low calorific value have strong negative linear correlation.The linear model of the two indexes w as built using the Linear Regression function of SPSS.The results show that the regression model can be used to forecast low calorific value of the coal seam.

calorific value,correlation analysis,regression model,SPSS

TQ533

A

广东省自然科学基金项目(10452404801006352);湛江师范学院博士专项研究项目(ZW 5611)

梅晓仁(1973-),男,博士后,讲师,现在湛江师范学院商学院从事企业管理、管理信息系统、矿业系统优化研究。

(责任编辑 张毅玲)