深水钻井隔水管纵横弯曲变形解析

李 妍,吴艳新,高德利

(中国石油大学石油工程教育部重点实验室,北京102249) *

深水钻井隔水管纵横弯曲变形解析

李 妍,吴艳新,高德利

(中国石油大学石油工程教育部重点实验室,北京102249)*

为了准确获得深水钻井隔水管的静力学响应,给出了任意连续横向载荷作用下隔水管静力学位移响应的解析解。首先将隔水管纵向离散成若干梁单元,建立单元任意连续横向载荷作用下隔水管静态控制方程;然后通过对控制方程进行降阶变换求得其特解,并由节点的连续条件及边界条件提出了此方程隔水管位移响应的解析解表达式;最后以矩形流作用下隔水管位移响应问题为例,定量计算了隔水管的最大横向变形及其位置,结果达到要求。

深水钻井;隔水管;解析解;位移响应

深水钻井隔水管受到波浪、流等复杂载荷的作用,因此隔水管响应分析及强度设计成为海洋石油钻采设备中亟需解决的重要课题之一。许多学者[1-3]建立了隔水管系统力学控制方程及隔水管响应计算方法,Mathelin[4]研究了隔水管涡激振动的位移响应计算方法,Simmonds[5]利用有限差分法给出了隔水管的响应,文献[6-7]运用有限元法及ANSYS软件对波流极值载荷作用下的深水钻井隔水管进行了非线性分析,这些研究方法均采用数值方法求解隔水管静力学控制方程。文献[8]给出了一部分外载荷形式作用下管柱静力学控制方程的解析解;Chaples[9]给出了隔水管静力学控制方程的解析解表达式,此解为级数形式,所以对于某些外载荷,其解可能会发散而不能给出正确的位移响应。本文的目的是提出任意连续横向载荷作用下隔水管静力学控制方程的解析解。首先建立了任意连续横向载荷作用下的隔水管静力控制方程,此方程的解包括齐次方程的通解和非齐次方程的特解,对隔水管进行纵向离散化,通过对梁单元静力控制方程进行降阶变换,求出任意外载荷下的特解形式;然后由节点的连续条件及边界条件提出此方程的隔水管位移响应的解析解表达式;最后通过矩形流作用下隔水管位移响应这一算例验证解析解的正确性。

1 任意连续横向载荷下隔水管位移响应

将受到顶部张紧力隔水管的数学模型简化为垂直平面内的梁在任意连续横向载荷作用下变形进行分析,如图1。

其静力学控制方程为[10]

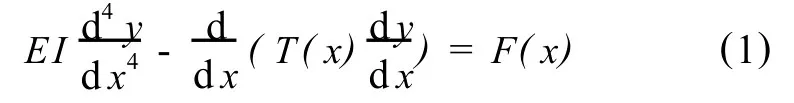
式中,EI为隔水管抗弯刚度,N·m2;F(x)为隔水管单位长度上所受任意连续横向载荷,没有固定载荷形式的限制,具有较为广泛的适用性;T(x)为隔水管任一点的有效轴向张紧力。

由于隔水管的轴向张紧力沿水深是变化的,所以任一点的有效轴向张紧力为

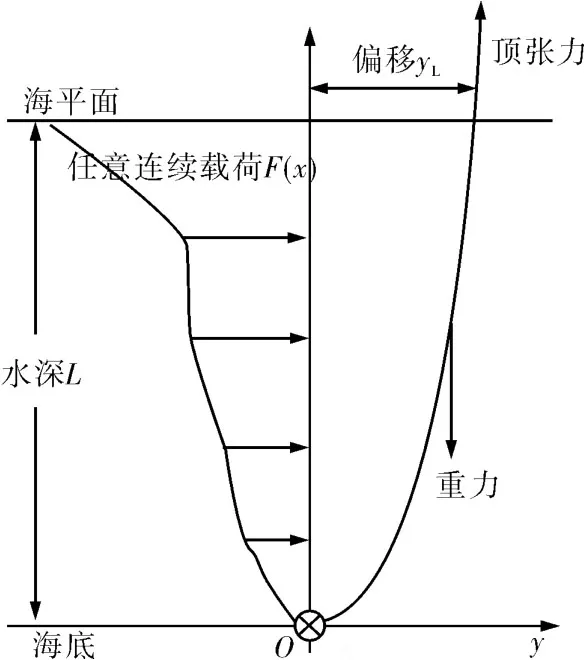
图1 深水钻井隔水管受力分析

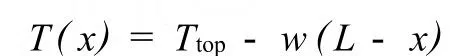
式中,Ttop为隔水管顶张力,N;w为隔水管单位长度的表观重力,N/m;L为水深,m。

令T*=,则式(1)变为

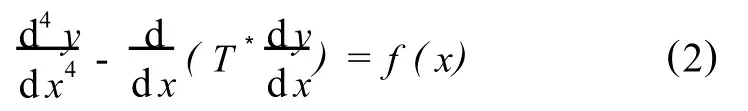
将隔水管纵向离散n等分,得到1,2,…,n个梁单元,同时得到n+1个节点,若单元总数 n选择的较大,则对于单元i可以假设 Ti+1=Ti,即离散单元受到纵向恒定拉力的作用,即

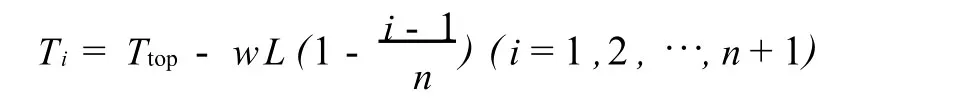
所以单元梁i的挠曲方程为

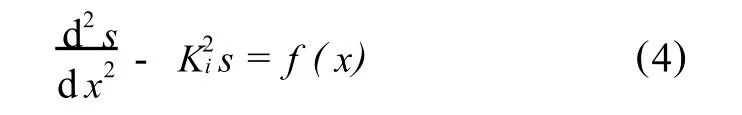
式(4)的解s由对应的齐次方程的通解s0和非齐次方程的特解s*组成,即s=s0+s*。显然,s0=

对式(4)进行降阶处理求特解s*。

令z=s′-Kis,则式(4)等效为

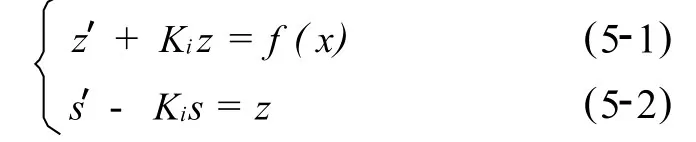
对式(5-1)求一特解为

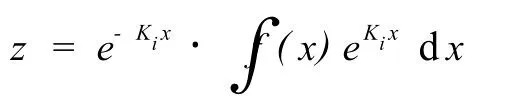
代入式(5-2),求出式(4)的特解为

采用分部积分法进一步整理得

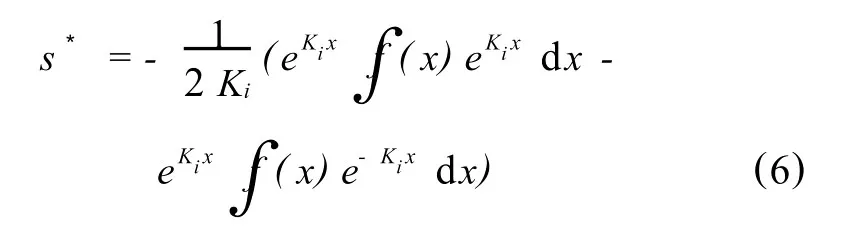
所以式(4)的解为

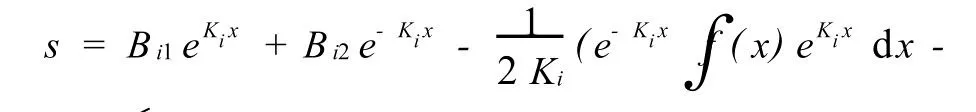
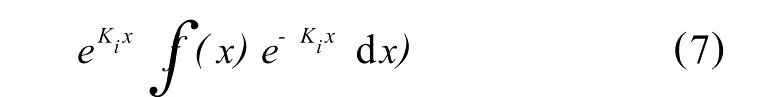
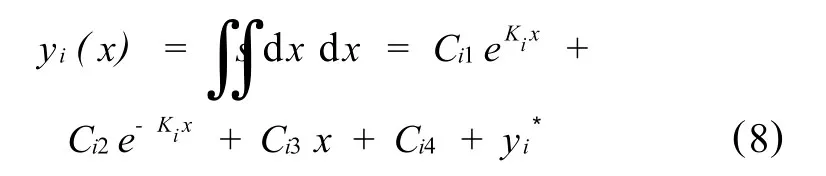
各单元的连续方程(以i节点为例)为

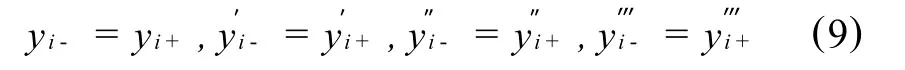
由连续条件,以i单元为例,运算后可得到各单元解析系数 Cij(i=2,…,n;j=1,2,3,4)之间的关系为

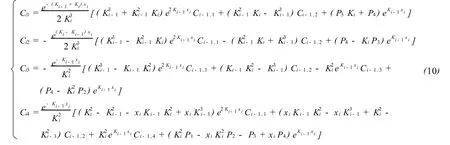
本文方法不限制某一特定边界条件。以建立隔水管模型为简支梁两端铰接这一边界条件为例,其边界条件为

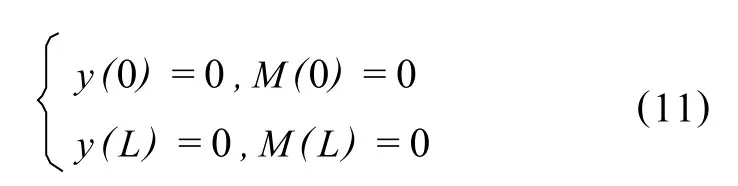
式中,y为隔水管的横向位移,m;M为隔水管的弯矩,N·m。

以i=2为例,用式(11)求解第1节点,有下面的关系,即

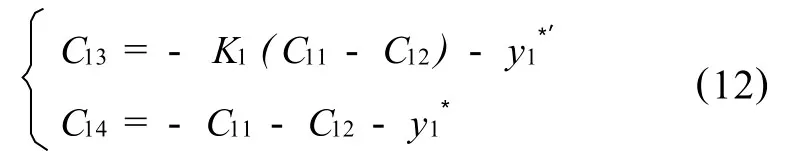
代入式(10)有

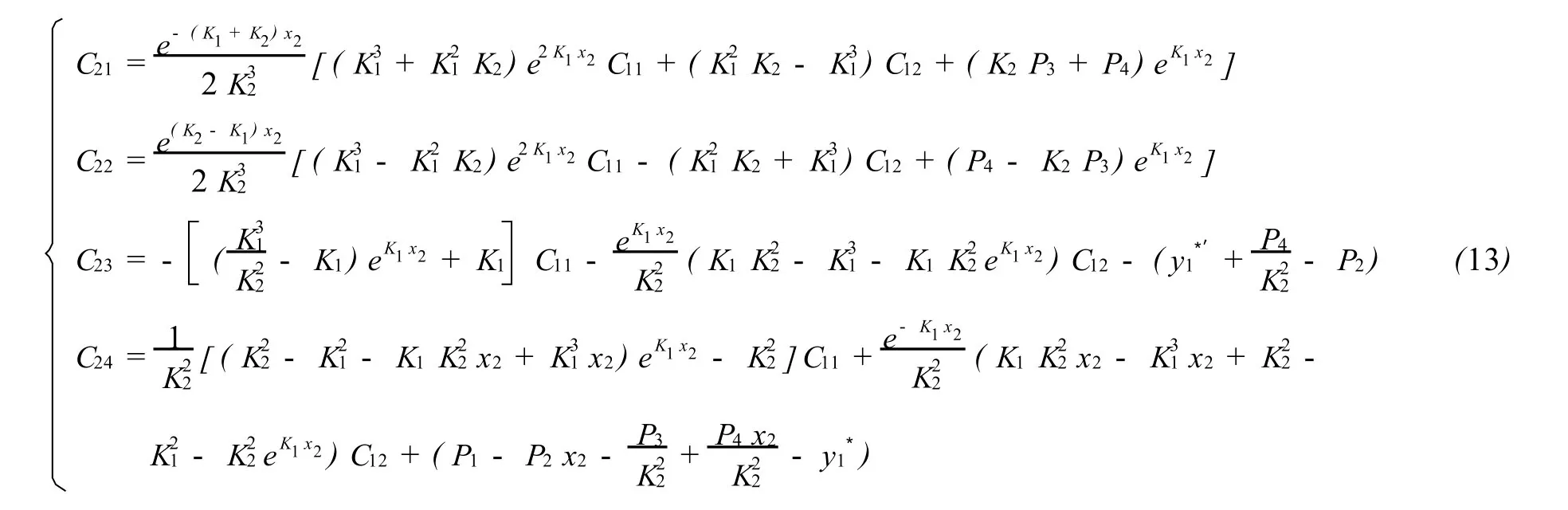
该结果表明,单元2的变形系数可用第1单元的待定系数C11、C12来表示,根据单元i与i-1的解析系数之间的关系式(10),依次类推可以得到单元i(1,2,…,n)的解析系数 Cij(j=1,2,3,4)由单元1的2个待定系数C11和 C12,即

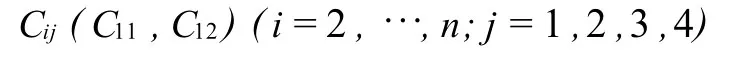
对于单元n变形的解析系数Cnj(j=1,2,3,4)应满足式(11)节点n+1处的约束,即

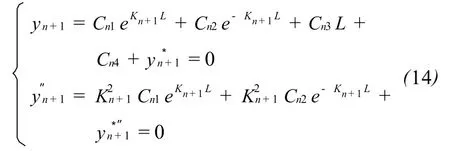
由式(10)、式(12)和式(14)联立,可得隔水管每一单元的变形系数,然后把每一单元的变形系数代入式(8),可得隔水管每一段的位移响应,整合后可得到隔水管整体位移响应。

2 算例分析

以矩形流剖面为例,隔水管长度为100 m,外径«0.508 m,壁厚0.025 4 m,不考虑隔水管的初始偏移,张力比为1.3,海水密度1 021 kg/m3,钢密度7 850 kg/m3,钻井液密度1 200 kg/m3,弹性模量206.8 GPa,拖曳力系数1.2,海平面流速为1.4 m/s。根据莫里森公式求得 F(x),并令 f(x)===B,由式(8)、式(10)、式(12)和式(14)编制MATLAB程序,得到矩形流剖面隔水管水平位移响应,如图2。

图2 隔水管横向变形

由图2可知,在矩形流外载荷作用下,用解析法求得隔水管的最大横向变形发生在距海底49 m处,最大横向位移为1.718 8 m;用有限差分法得出的隔水管最大横向变形发生在距海底48 m处,最大横向位移为1.719 8m。由此可见,2种方法得出的计算结果很相近,而解析解更便于推广应用。

3 结论

1) 通过将隔水管纵向离散化,对其梁单元静态控制方程进行降阶变换求出其特解,并进一步给出梁单元方程的解析解表达式,整合后得到了隔水管在任意横向载荷下的水平位移响应解析表达式。

2) 以矩形流外载荷的隔水管为例,计算出隔水管的横向位移响应,其最大横向变形及位置的计算结果与有限差分法很接近,而本文的解析解更便于推广应用。

[1] 李华桂.海洋钻井隔水管的动力分析[J].石油学报, 1994:16(1):84-88.

[2] Burke B G.An analysis of marine risers for deep water [J].petroleum technology,1974,26(4):455-465.

[3] Ertas A,Kozik T J.Philosophy and principle of riser modeling and numerical approaches[C].Offshore operations symposium,1986.

[4] Mathelin L,de Langre E.Vortex-induced vibrations and waves under shear flow with a wake oscillator model[J].Mechanics B/Fluids,2005(24):478-490.

[5] Simmonds D G.Dynamic analysis of the marine riser [G].SPE 9735-MS,1980.

[6] 石晓兵,陈 平.三维载荷对海洋深水钻井立管强度的影响分析[J].天然气工业,2004(12):86-88.

[7] 王海峡,赵广慧.波流极值载荷作用下隔水管的非线性分析[J].石油矿场机械,2008,37(11):6-10.

[8] 高德利.油气井管柱力学与工程[M].北京:中国石油大学出版社,2006.

[9] Chaples P.Sparks.Fundamentals of marine riser mechanics:Basic principles and simplified analyses[M]. Penn Well Corporation,2007:281-283.

[10] 畅元江,陈国明,孙友义,等.深水钻井隔水管的准静态非线性分析[J].中国石油大学学报:自然科学版, 2008,32(3):114-118.

Analytic Solution of Flexural Deformation of Deep-water Drilling Riser

LI Yan,WU Yan-xin,GAO De-li
(MOE Key L ab ofPetroleum Engineering,China University ofPetroleum,Beijing102249,China)

The analytic solution of static displacement response of riser under arbitrary continuous transverse loads is given in order to accurately obtain the static response.First,the riser is divided into a number of discrete beam elements.The governing equation of the unit riser under arbitrary continuous transverse loads is established.Then the order for governing equation is reduced in order to obtain its special solution.The expression of analytic solution of displacement response is presented by the continuity condition and boundary conditions of the nodes.Finally,the maximum lateral deformation and its position of the riser with rectangular current are calculated as an example,which is a satisfactory result.

deep-water drilling;drilling riser;analytic solution;displacement response

1001-3482(2011)07-0021-04

TE952.01

A

2011-0-0

李 妍(1978-),女,黑龙江哈尔滨人,讲师,博士,从事结构动力试验技术及结构控制研究,E-mail:liyancup @cup.edu.cn。