水平轴风力机气动性能研究

李成本，高德忠

风力机气动性能计算除了与叶片本身的气动外形有关外，还与流经其叶轮的气流形式有关。由于气流的不定常性，所以很难用精确的模型进行模拟。目前主要采用基于空气动力学理论的动量-叶素理论、涡流理论和计算流体力学 (CFD)[1]、[2]等等。

动量-叶素理论基于绕旋转风机叶片的流动气体是二维、定常流的假设，将叶片沿展向分成许多叶素，通过引入轴向诱导因子a和周向诱导因子b，推导出叶素上推力系数、扭矩系数和功率系数的表达式。

涡流理论和计算流体力学（CFD）是近年来才应用于风力机气动性能计算的新方法，虽然其分析理论更贴近于风力机的实际工作状态，但是由于计算过程比较繁冗，在一些关键技术上还不够成熟，目前还不能作为风力机气动性能设计和计算的工具。

1 气动计算基本模型

叶片气动性能计算主要包括三部分，即功率与功率系数、转矩与转矩系数、轴力与轴力系数。通过功率的计算可以判断风机发电能力的强弱；由转矩计算结果决定主轴尺寸以及匹配的发电机功率类型；由于轴力通过轮毂最终作用到塔架上，而塔架的结构与刚度设计是风机设计中的关键部分，故轴力又是风机设计中的一个重要载荷依据。因此气动性能计算研究不仅仅对风轮叶片设计至关重要，而且对风电机组整机设计都是必不可少的。

1.1 动量理论

动量理论是将风轮简化成一个“制动盘”，并且通过风轮的气流简化为理想的流管（见图1）。

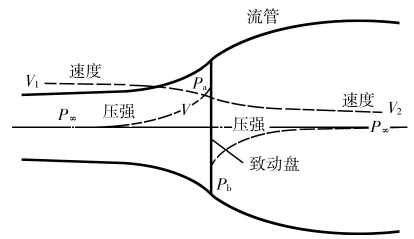
图1 风轮流动的单元流管模型

在该模型中，定义轴向诱导因子a和周向诱导因子b分别为

式中，WX—轴向诱导速度（m/s）；V1—风轮上游风速（m/s）；WY—风轮叶片半径r处的周向诱导速度（m/s）；Ω—风轮转动角速度（rad/s）。

结合轴向诱导因子a和周向诱导因子b，定义W为叶片r处诱导速度，方向与升力方向相反[3]，则

式中，φ—入流角（°）。

应用动能定理和伯努力方程，作用在整个风轮上的轴向力 (推力)T和转矩M可分别表示为

式中，ρ—空气密度（kg/m3）；R—叶轮半径（m）。

1.2 叶素理论

叶素理论的基本出发点是将叶轮叶片沿展向分成许多微段，称这些微段为叶素。该理论假设每个叶素上的气流相互之间没有干扰，即叶素可以看成是二维翼型。通过将作用在每个叶素上的力和力矩沿展向积分，即可求得作用在整个叶轮上的力和力矩（见图2）。

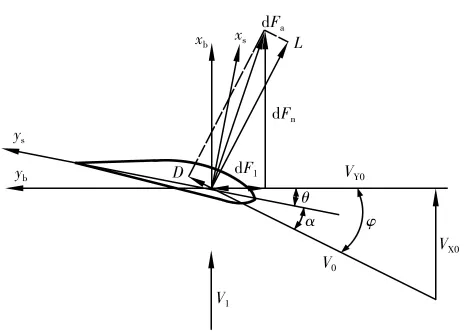
图2 速度三角形和空气动力分量

对每个叶素来说，其速度可以分解为垂直于风轮旋转平面的分量VX0和平行于风轮旋转平面的分量VY0，φ为入流角，α为攻角，θ为叶片在叶素处的几何扭角。由动量理论可知

则叶素处的合成气流速度

叶素处的入流角φ和攻角α分别为

而由合成气流速度V0引起的作用在长度为dr叶素上的空气动力dFa可以分解为法向力dFn和切向力dFt，则有

式中，c—叶素剖面弦长（m）；Cn、Ct—分别表示

法向力系数和切向力系数。即

式中，Cl、Cd—分别表示叶素的升力系数和阻力系数。

此时，作用在风轮平面上的轴向力T和扭矩M可分别表示为

式中，B—叶片数。

1.3 动量-叶素理论

动量-叶素理论是将动量理论和叶素理论相结合，计算出风轮旋转平面中的轴向诱导因子a和周向诱导因子b，再利用T动量=T叶素和M动量=M叶素，并根据图2中的速度三角形得到

2 模型修正

2.1 Prandtl叶尖损失修正

在实际风机运行中，风力机的叶片数是有限的（一般为3个），由于叶片上下表面有压力差，当叶片旋转时，在叶尖处的气流会产生绕流，从而引起力矩的减小。因叶尖处的叶素受力对风机的性能有很大影响，所以叶尖处的损失不容忽视。Prandtl对叶尖的空气流动做了研究，并定义叶尖修正系数为

则式 （18）、 （19） 可表达为

当风轮叶片部分进入涡环状态时，动量方程不再适用，应对动量-叶素理论进行修正。

（1） 当轴向诱导因子a>0.2时，采用Glarert修正法，a由下式确定

（2） 当轴向诱导因子a>0.38时，采用Wilson修正法，式（21） 由

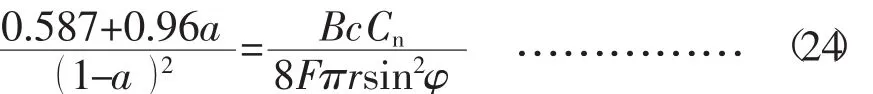
代替。

这样，根据上面的关系式就可以通过迭代的方法求得轴向诱导因子a和周向诱导因子b，迭代步骤如下：

（1） 设定a，b的初始值，一般可取0。

（2） 根据式 （10） 和 （11） 分别求出入流角 φ和攻角α。

（3）根据翼型空气动力特征曲线得到叶素的升力系数Cl和阻力系数Cd。

（4） 根据式 （14）和（15） 求出法向力系数Cn和切向力系数Ct。

（5） 根据式 （20） 求出叶尖损失因子F。

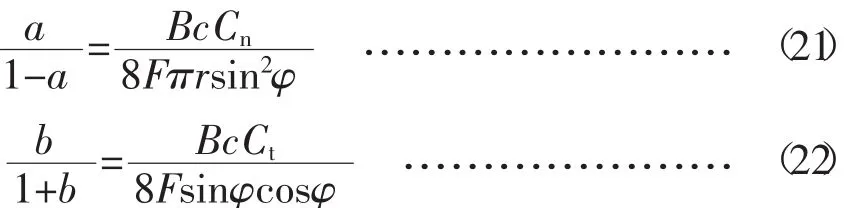
（6） 根据公式 （21）、 （22） 计算出 a和 b，若a>0.2，则根据公式（23） 重新计算；若a>0.38，则根据公式（24）重新计算。

（7） 比较新计算的a和b值与上一次的a和b值，如果误差小于设定的误差值 (一般可取0.001)，则迭代终止；否则，再回到步骤（2） 继续迭代。

2.2 叶片三维效应

动量-叶素理论是基于气流绕旋转风轮叶片上的流动是二维的假设，然而实际旋转风轮叶片上的气流流动是三维的，虽然通过一些修正方法，使该理论在计算叶片气动性能上是可信的，但这必须通过翼型数据的可靠性来保证。Prandtl叶尖损失系数可以补偿叶片尖部三维流动的影响，对于给定的叶片，仍可以采用其表面上气流流动的二维假设。在风机的实际运行中，风机叶片经常工作在深度失速状态下，特别是失速控制型的风机，所以风机叶片处于低攻角区域部分的气动数据很难得到，而且当叶片转动时，由于离心力和科氏力的作用，使叶片表面边界层减薄，分离点位置后移，都会改变翼型二维数据的特性。因此还需要对现有的翼型数据进行修正来适应深度失速和叶片转动的工况。

Snel采用有粘/无粘迭代的方法求解叶片上的准三维边界层积分方程，并通过与翼型的风洞试验结果进行比较，得到三维效应对升力系数的修正公式

式中， （Cl）p=2π （ α- α0），α0—翼型的零升力迎角（rad）；c—弦长（m）。

Corrigan在Snel模型的基础上得到一个新的失速延迟模型。该模型用于对升力和阻力系数进行三维效应修正时，可分别表示

2.3 叶片动态入流

应用动量-叶素理论时是假设桨盘上诱导速度的分布是均匀的，而实际上风力机尾涡诱导速度是不均匀的，即使来流是均匀定常流，当其经过风轮叶片时将变为不均匀的定常流。

通常风力机的尾流模型有平衡尾流模型、冻结尾流模型和动态如流模型三种。

平衡尾流模型假设尾流连同诱导速度流场对叶片受载的变化即刻就有反应。而冻结尾流模型是假设诱导流场完全独立于有关风况和叶片受载的变化。严格来说，在现实中这些处理方式都不恰当。由于自然风的风速大小和方向是随时变化的，而且当叶片上的载荷发生变化时，会影响到风力机尾流中的旋涡状态，而所有的这些变化的效果需用一定的时间来改变诱导流场，是一个动态过程[4]。因此诱导速度W随时间的变化可表示为

式中，Wint—中间值；W—最终修正诱导速度；Wqs—准静态解；k=0.6，τ1、τ2—时间常数，具体可表达为

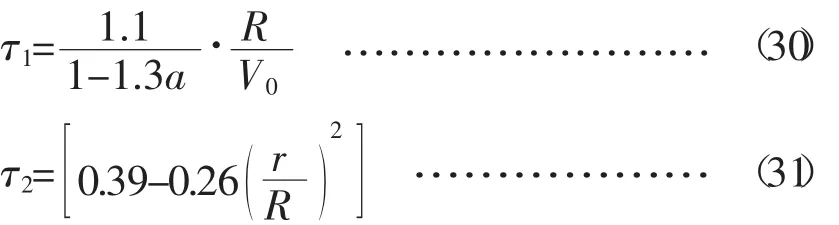
这样通过对诱导速度进行修正，即可得到修正后的a和b值，并求出风力机各性能参数的最终修正值。

通过试验Tjaereborg风机主轴转矩的计算值和测量值随桨距角变化的曲线可以发现，在t=2 s时桨距角由0°增加到3.7°，主轴扭矩首先从260 kN·m降到150 kN·m，直到10 s之后诱导速度和转矩才重新建立平衡。而在t=32 s时桨距角又减小到0°，扭矩则在首先增大后再逐渐达到平衡状态（见图3）。而图中峰值的衰减只能通过动态如流模型计算出。因此该模型对于变桨风机尤其重要。

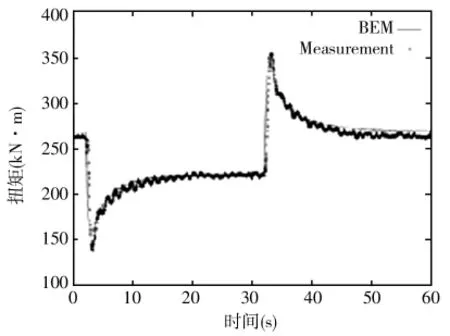
图3 扭矩-桨距角变化曲线

2.4 动态失速

受风切变、塔影效应和湍流等因素的影响，气流在叶片前缘的驻点会经常改变。因此在风轮的旋转过程中，叶片的攻角亦会随之改变，其失速迎角比翼型静止时的失速迎角要大，而且翼型空气动力特性随迎角变化的曲线会出现迟滞现象，这种现象被称为动态失速。因叶片攻角的改变不会在载荷中立即显示出来，而是有一个时间延迟，且该延迟与弦长和叶片截面处的相对速度成正比，而对应产生的气动载荷的变化则取决于边界层是否附着或者已经部分分离。Beddoes-Leishman模型是对二维叶片进行动态气动计算比较成熟的模型，充分考虑了附着流、前缘分离和空气可压缩性的影响，并且修正了推力系数和力矩系数[2]。在风机建模中，从稳定性方面考虑，至少应对其升力建立动态失速模型。对风力机而言，后缘分离被认为是最重要的动态失速现象，可以通过S.Øye教授所描述的分离函数fs来确定动态失速的程度

式中，Cl,inv—没有任何分离的非黏性流动升力系数；Cl,fs—已经完全分离的流动的升力系数；τ—时间常数，；c—局部弦长 （m）；

V0—叶素处的合成气流流速（m/s）；A—常数，典型值取4。

在方程（33） 中，假定fs总是试图回归到静态值，估算 Cl，fs和的一种方法可参见[5]。

3 结语

动量-叶素理论是目前风力机进行气动性能设计和计算的基本理论，该理论假设绕风力机叶片的气流是二维定常的，而实际上流经叶片的气流具有三维非定向性，所以在使用动量-叶素理论时应当考虑到叶片的三维效应、动态入流和动态失速等各种因素对风力机性能的影响，通过对相关参数进行修正，从而使计算结果达到可接受的程度。

[1]李军向.大型风机叶片气动性能计算与结构设计研究.武汉理工大学，2008.

[2]张仲柱.水平轴风力机叶片气动性能计算模型研究.中国科学院研究生院，2007.

[3]Martin.O.L.Hansen.Aerodynamics of Wind Turbines.北京：中国电力出版社，2009.

[4]M.O.L.Hansen,J.N.S?rensen,S.Voutsinas,etc.State of the art in wind turbine aerodynamics and aeroelasticity.Progress in Aerospace Scineces 2006,42:285-330.

[5]Hansen MH,Gaunaa M,Madsen HA.A Beddoes–Leishman type dynamic stall model in state-space and indicial formulations.Risoe-R-1354(EN),2004.