一种4m阶幻方的构造方法
2011-12-09聂春笑
聂春笑
(合肥工业大学 管理学院,安徽 合肥 230009)
一种4m阶幻方的构造方法
聂春笑
(合肥工业大学 管理学院,安徽 合肥 230009)
给出一个双偶数阶幻方的构造方法,并证明按照这种方法构造出的幻方具有四阶幻方类似的性质,同时这类幻方具有特别的对称性.
双偶数阶幻方;构造;四阶幻方
杨辉在其1275年成书的《续古摘奇算法》上卷里面给出了两个四阶幻方并指明其中的阴图的构造方法(这里只给出其中的阴图,如矩阵(1)所示,本文的幻方均用矩阵形式表达)为“以十六子依次第作四行排列.先以外四角对换一换十六,四换十三,复以内四角对换六换十一,七换十”[1].丢勒在其的著名铜版画《忧郁》里也出现了一个神秘的四阶幻方(如矩阵(2)所示),特别的,其最后一行中间的两个数字组合1514为这幅画的创作年份.关于这两个幻方的讨论已经有很多了.这里要提及的是一个它们均具有的特别性质,即对角线上的元素平方之和等于非对角线上的元素平方之和,对角线上的元素的立方之和等于非对角线元素的立方之和.

由于四阶幻方的对角线元素与非对角线元素的个数是相等的,因此我们进一步猜测应该是存在一般的对角线元素与非对角线元素之间的关系满足(3)、(4)式的双偶数阶幻方.
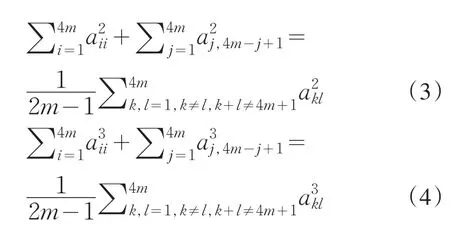
当4m=4(也即2m-1=1)的时候就是上面我们说的杨辉与丢勒的幻方所给出的性质.这个性质看起来比较苛刻,但实际上我们可以构造多种方法来满足上述要求,并且还有大量的幻方满足这个性质.本文仅就一种较特殊的方法给出证明.
1 一种构造双偶数阶幻方的方法
双偶数阶幻方的构造方法多种多样,在一些中文专著上均有一些较经典的方法[2-4],而在大量的论文中也给出了双偶数阶幻方的构造方法,这里不再一一列举.其中在文献[3]中给出了一种称为“调换对称行、列法”的双偶数阶幻方的构造方法,本文将这个方法进行推广,并给出完整证明.
方法:
(1)将1…(4m)2按照从左到右,从上到下按大小排列成一个方阵(如矩阵(5)所示),记为方阵M=(ai)j;
(2)从1…2m中任取m个数字,不妨记为i1,i2…im,再从2m+1…4m中对偶的选取m个数4m-i1+1,4m-i2+1…4m-im+1,将这2m个数总括为一个集合,记为T1={i1,i2…im,4m-i1+1,4m-i2+1…4m-im+1};
(3)对于T1中的元素i,将方阵M=(ai)j中的对应的行(或列)倒置,否则则该行(或列)保持不变,形成方阵M=();
(4)类似(2)中的方式,再选取2m个数,做成集合T2={j1,j2…jm,4m-j1+1,4m-j2+1…4m-jm+1},其中T1与T2可以相同,也可以不同;
(5)对于T2中的元素j,将(3)中形成的方阵M=)对应的列(或行)倒置形成M=).
为简便,上述方法中的T1与T2称为变换集.
2 证明
下面给出上面的方法的证明.根据上述的构造方法,我们可以轻易的追溯对于M2中的元素在初始方阵M=(ai)j中的位置,而对于M中的任意元素都有一个表达式,因而用这种回溯的方式可以把M2中的行列元素之间的运算转化一般的数字计算.
对于上面的构造方法,有如下两条数字的变换规则,这里选取首先进行行变换再进行列变换的情形进行说明:
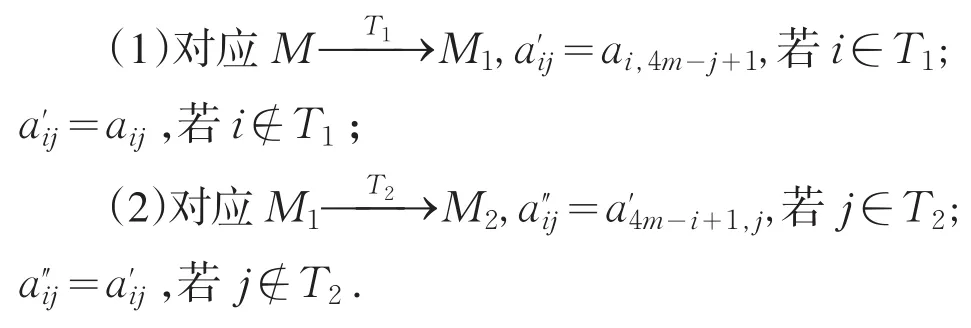
下面分别验证M2的确满足我们所要求的条件,首先证明其满足幻方的条件,然后再证明其满足前面所提到的两个条件.
(1)这里只证明对于M2,其的行元素之和为幻和,对于列与对角线的验证是类似的.对于M2的第i行,不妨设i∈T1,(其他情形类似的处理),则有等式
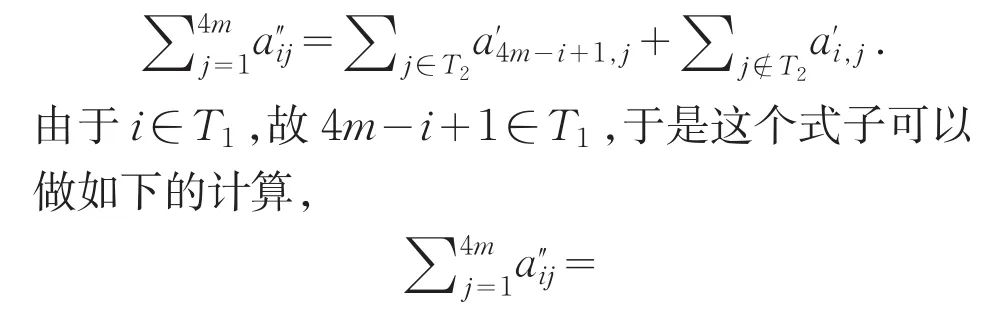
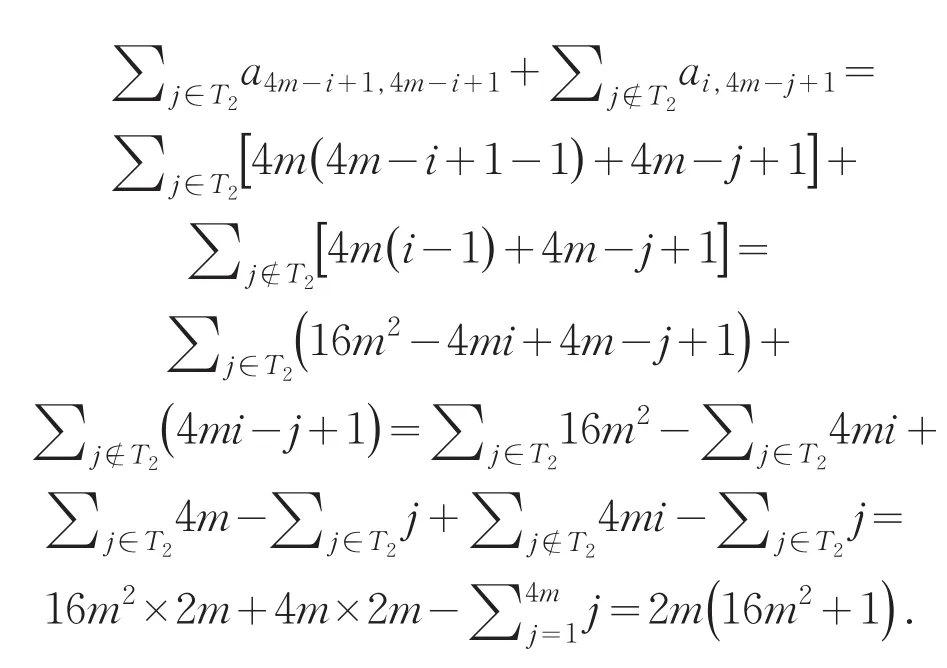
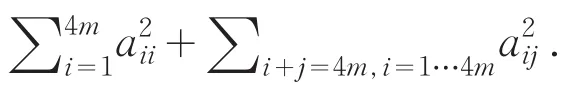
对于上面两个求和项分别计算如下,

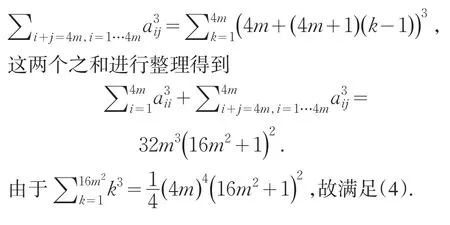
3 一个例子
下面给出一个8阶幻方的构造的例子,首先构造如(5)所示的方阵,

可以直接验证上述的方阵的确满足我们的要求.事实上这种基于对称构造的幻方还有很多其他的性质,比如在上面的例子中如果取变换集T2={1,4,5,8}或者T2={2,4,5,7}的话那么最后形成的幻方的中间将存在一个四阶子幻方.对于高阶时的结果是类似的,并且如果取一些特殊的变换集时将会出现多个子幻方的嵌套.
4 其他的初始方阵
对于上述的方法可以以不同的形式推广开来,下面仅就改变初始方阵的形式来给出一些小小的改进.改变初始方阵为其他类型的初始方阵而不改变具体的操作过程的话也可以得到幻方.下面给出具体的几个形式.
将初始方阵分割为若干同阶的小方阵并按照一定规律排列也可以获得幻方,下面以8阶幻方的构造为例,首先给出由2×2方阵排列的初始方阵如(8)所示,(9)即为对应构造出的幻方,变换集选取和上面的例子一致,下面的变换集选取均与上面例子中的一致.

也可以用4×4方阵进行类似的排列,如(10)即为一种排列方式,(11)为对应的幻方,若与(5)类似,但是每行均用公差为d|4m的等差数列也可以获得合适的初始方阵,如(12)所示的即为公差为2的初始方阵,(13)为对应形成的幻方.


若将(12)中的任意若干对偶的行(或列)交换则依然可以作为一个初始阵,比如1行与8行交换,4行与5行交换,则最后形成的幻方是由(13)的对应的幻方1行与8行交换,4行与5行交换形成的.

5 幻迹
上世纪初,建筑师C.F.布拉顿发现将幻方中的数字依次连接,可以获得一些对称的图案,这种图案称为幻迹(也称为幻直线).
由于上面的方法是对称式的构造幻方的,因而对应的幻迹也呈现出很好的对称性,下面仅给出(7)对应的幻迹,见图1.
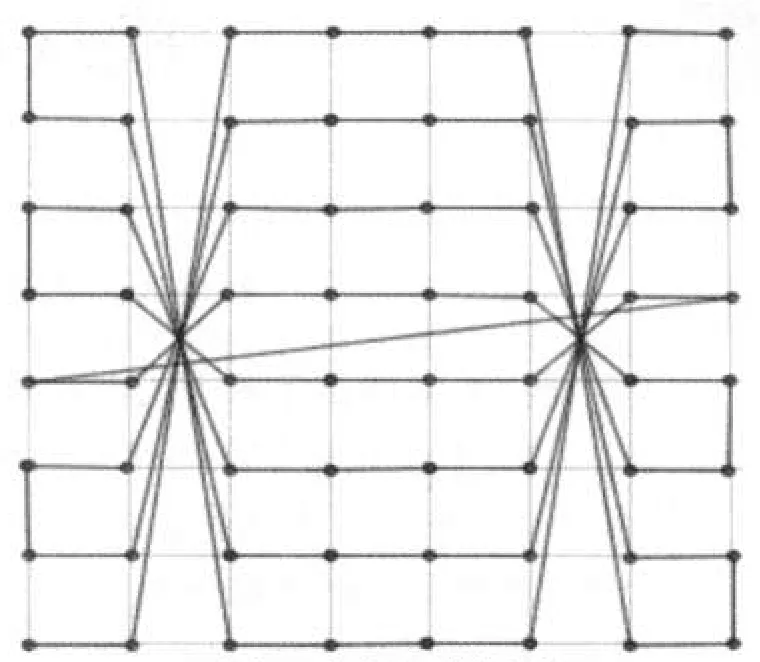
图1 幻方(7)的幻迹Fig.1The locus of magic square(7)
6 结论
本文给出了一种对称式构造双偶数阶幻方的方法,并证明了其具有和杨辉与丢勒在《续古摘奇算法》以及《忧郁》中给出的4阶幻方类似的性质.这类方法可以构造大量的幻方,并且这类幻方具有非常对称的幻迹.除了证明的情形外,一些其他形式初始方阵在具体方法不变的前提下也可构造出幻方,一般的规律与证明还需要进一步的研究.
[1]孙宏安.杨辉算法[M].沈阳:辽宁教育出版社,1997:384-385.
[2]吴鹤玲.幻方及其他[M].北京:科学出版社,2004:50-72.
[3]舒文中.幻方[M].广州:广东科技出版社,1991:2-41.
[4]欧阳录.幻方与幻立方的当代理论[M].长沙:湖南教育出版社,2004:67-84.
A Construction Method for the Magic Square of Order 4m
NIE Chunxiao
(School of Management,Hefei University of Technology,Hefei230009,China)
A method was given to construct the doubly even order magic square,and it was proved that the magic square constructed by this method have the similar properties with the magic squares of order four,and these magic squares have symmetrical properties.
doubly even order magic square;construct;magic square of order 4
O 157
A
1674-4942(2011)03-0270-04
2011-04-25
毕和平
