Efficient Methods for Solving the Initial-value Problem of the Ordinary Differential Equation

JIANG Zhaomin，LI Xiaojing

（School of Mathematics and Physics，Jiangsu Teachers University of Technology，Changzhou 213001，China）

Efficient Methods for Solving the Initial-value Problem of the Ordinary Differential Equation

JIANG Zhaomin，LI Xiaojing

（School of Mathematics and Physics，Jiangsu Teachers University of Technology，Changzhou213001，China）

We applied the variational iteration method and the homotopy perturbation method to solve the initial-value problem of the fourth-order ordinary differential equation.A comparison of the results with the exact solution illustrates that the approximation is of high accuracy.This confirms that the variational iteration method and the homotopy perturba⁃tion method are extremely efficient and simple to solve the initial-value problems.

variational iteration method；homotopy perturbation method；initial-value problem；exact solution；approx⁃imate solution

CLC mumber:O 241 Document code:A Article ID:1674-4942（2011）04-0370-05

In this paper,we consider the general fourth-or⁃der initial-value problem of the type

Wherefis continuous function on[a，b]and the parametersαi（i=1，2，3，4）are real constants.Such type of systems arise in the mathematical modeling of the viscoelastic and inelastic flows,deformation of beams and plate deflection theory[1-2].Various meth⁃ods such as the variational iteration method（VIM）[3-5]，the homotopy perturbation method（HPM）[6-7]and Adomian decomposition method[8]were de⁃veloped for solving the boundary value problems of the ordinary or the partial differential equation.

The purpose of this article is to use the analysis of the variational iteration method and the homotopy perturbation method for solving the initial-value prob⁃lem of the fourth-orde r ordinary differential equation（1）-（2）.

1 Analysis of VIM

We can construct the following iteration formula⁃tion：

We can takeu0（t）with some confirmable param⁃eters，then substituting it into（7），we getu1（t）.Re⁃peating the process，we can getu2（t），u3（t），…，un（t）.Applying the initial conditions，the values of the pa⁃rameters can be determined.

Here we suppose

If the first-order approximate solution is enough,Imposing the initial conditions（4），we can identify the unknown constants as follows:

So we obtain the following first-order approxi⁃mate solution

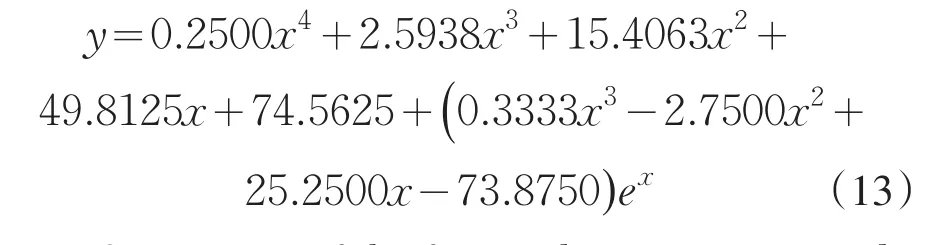
Comparison of the first-order approximate solu⁃tion Eq.（13）with the exact solution

Eq.（5）is illustrated in Fig.1

From the fig1，we can see intuitively the curve of the approximation by VIM close to the curve of the exact solution.By means of the mathematical software MATHEMATICA，we can obtain its second-order or third-order approximations with very high accuracy easily.

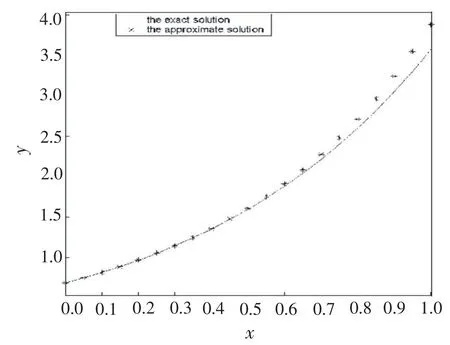
Fig.1Comparison of the approximate solution obtained by variation iteration method with the exact solution

图1 变分迭代近似解和精确解的比较

2 Analysis of HPM

Fig.2Comparison of the approximate solutions obtained by HPM with the exact solution图2 同伦摄动近似解和精确解的比较

We compare the approximate solutions obtained by HPM with the exact solution，and it is clear from Fig.2 that the fifth-order approximate solution is in good agreement with the exact solution.Also it is to be noted that the accuracy can be improved by com⁃puting more terms of the approximate solutions.

3 Conclusion

In this paper，we have used the variational itera⁃tion method and the homotopy perturbation method to solve the initial-value problem of the fourth-order or⁃dinary differential equation.The example illustrates that even its first-order approximation obtained by VIM is of high accuracy，the fifth-order approxima⁃tion by HPM is of high accuracy.The obtained solu⁃tion shows that these methods are very convenient and effective for solving the initial-value problems.These methods provide with realistic series solutions that converge very rapidly in physical problems.Hence，it is concluded that VIM and HPM can be used as effi⁃cient and reliable alternative algorithms for solving the initial-value problems of the ordinary differential equation.

[1]Chawla M M,Katti C P.Finite difference methods for two-point boundary-value problems involving higher or⁃der differential equations[J].BIT,1979,19:27-33.

[2]DoedelE.Finite difference methodsfor nonlinear two-point boundary-value problem[J].SIAM Journal of Numerical Analysis,1979,16:173-185.

[3]He J H.Variational iteration method-Some recent results and new interpretations[J].Journal of Computational and Applied Mathematics2007,27:3-17.

[4]He J H,Wu X H.Variational iteration method:New de⁃velopment and applications[J].Computers and Mathemat⁃ics with Applications,2007,54:881-894.

[5]Muhammad Aslam Noor,Syed Tauseef Mohyud-Din.An efficient method for fourth-order boundary value problems[J].Computers and Mathematics with Applications,2007,54:1101-1111.

[6]Noor M A,Mohyud-Din S T.An efficient algorithm for solving fifth-order boundary value problems[J].Mathe⁃matical and Computer Modelling,2007,45:954-964.

[7]Golbabai A,Javidi M.Applications of He’s homotopy per⁃turbation method for th-order integro-differential equa⁃tions[J].Applied Mathematics and Computation,2007,190:1409-1416.

[8]Wazwaz A M.The numerical solution of fifth-order boundary-value problems by Adomian decomposition[J].Journal of Computational and Applied Mathematics,2001,136:259-270.

求四阶常微分方程初值问题近似解的有效方法

姜兆敏，李晓静

（江苏技术师范学院 数理学院，江苏 常州 213001）

运用变分迭代法和同伦摄动方法求解四阶常微分方程初值问题的近似解，通过将近似解和精确解进行比较，验证了变分迭代法和同伦摄动方法对求解常微分方程的初值问题是两种既有效又简便的方法.

变分迭代法；同伦摄动法；初值问题；精确解；近似解

2011-09-03

江苏省自然科学基金（BK2009105，BK2008119）；江苏省高校自然科学基金（09KJD110001，08KJB110011）

毕和平