定积分的三角Hermite插值小波算法

卢 超，沈有建

（海南师范大学 数学与统计学院，海南 海口 571158）

定积分的三角Hermite插值小波算法

卢 超，沈有建

（海南师范大学 数学与统计学院，海南 海口 571158）

本文给出了一种求一般函数的定积分的小波方法.首先介绍了三角Hermite插值小波及其相关性质，利用三角Hermite型插值小波算子定义，推导出了求一般函数的定积分的计算公式，给出算例，结果表明此算法具有较高的精确度.

三角Hermite插值小波；定积分；数值解

随着小波理论的发展，小波方法不仅应用微分方程的数值求解，还可以用于定积分的计算，求函数定积分的数值方法有很多种，常见的方法如梯形公式、辛普森公式、Simpson法等.文献[1]利用三角Hermite型插值算子的定义推导出了求一般三角函数的定积分计算公式.本文在此基础上，结合小波空间与尺度函数空间的关系，给出一个求一般函数的定积分的计算公式.最后应用此数值计算公式与Simpson求积法公式所得出的计算结果进行比较.

1 三角Hermite插值小波及其基本性质

下面简略地介绍三角Hermite插值小波及其基本性质（参见[2]）.Quak构造了两个尺度函数和两个小波函数，这些尺度函数和小波函数在区间[0 ,2π]上的节点

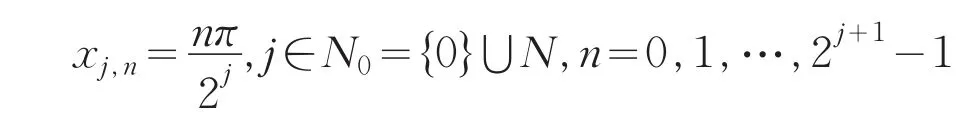
满足Hermite插值性质.

首先我们引进一些记号，令N表示全体自然数集，Z表示全体整数集，N0={}0 ⋃N.对l∈N,Tl表示阶数为l的三角多项式组成的线性函数空间.

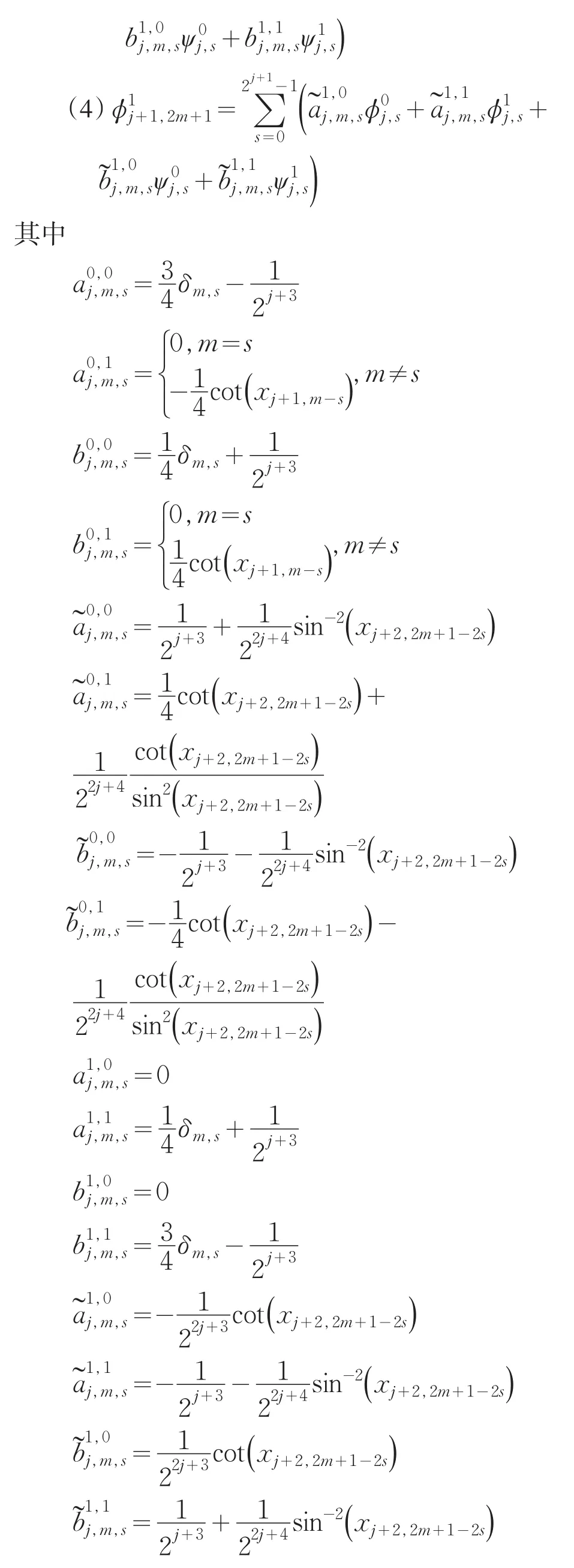
2 定积分的小波算法

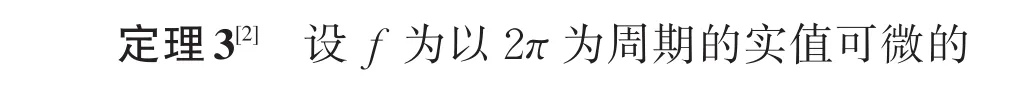
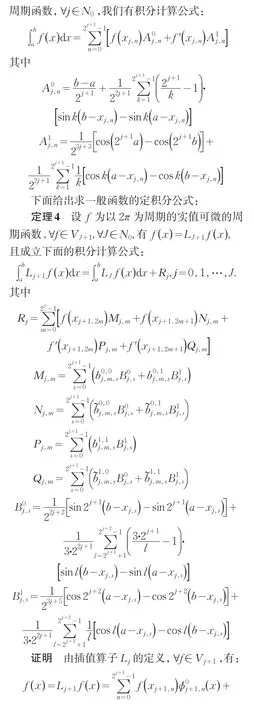
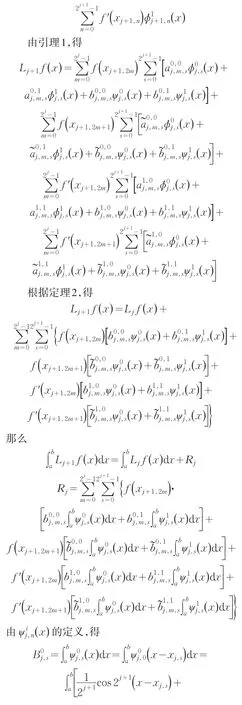
3 数值算例

我们通过实例来说明定理4中给出的计算公式的有效性.

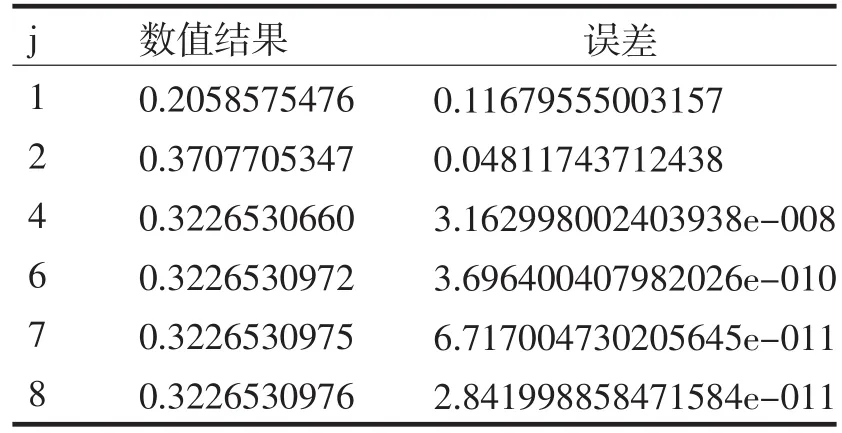
表1 算例的数值计算结果Tab.1Calculating results of numerical example

从本例子的精确值为：0.32265309765483，调用Matlab中的Simpson求积公式，得到的数值解为：0.32265310780303.从上表可以看出，当越大时，计算出的数值结果越接近精确值，比Simpson求积法求出的结果更准确，从而说明此算法的精确度很高.

[1]李健.微分方程的三角Hermite插值小波方法[D].海南:海南师范大学,2010.

[2]Quak E.Trigonometric Wavelets for Hermite Interpolation[J].Mathematics of Computation,1996,65(214):683-722.

The Trigonometric Hermite-type Interpolation Wavelet Method for the Evaluation of Integrals

LU Chao，SHEN Youjian

（College of Mathematics，Hainan Normal University，Haikou571158，China）

In this paper,we use trigonometric Hermite-type interpolation wavelet operator to derive the computing for⁃mula of integrals of general functions.At the end of the paper,the method was tested by the numerical example.

trigonometric Hermite-type interpolation；integrals；Numerical integration

O 175.1

A

1674-4942（2011）01-0028-04

2010-12-17

海南省自然科学基金项目（109001）；海南师范大学应用数学重点学科基金项目

毕和平