关于消去图的一个充分条件*
2011-12-08宋强
宋 强
(潍坊学院,山东 潍坊 261061)
0 引言
本文所考虑的图均指有限无向简单图。设G是一个图,分别用V(G)和 E(G)表示图G的顶点集和边集,用 dG(x)表示顶点 x在G中的度数。设 g和f是定义在V(G)上的非负整值函数,并且对于任意的 x∈V(G)有 g(x)≤f(x)。图G的一个(g,f)-因子是 G的一个支撑子图 F,使对任意的 x∈V(G),有 g (x)≤dF(x)≤f(x)。
特别地,若图G本身是一个(g,f)-因子,则称G是一个(g,f)-图。如果去掉图 G的任何三条边都有一个(g,f)-因子,则称图 G是一个(g,f)-3-消去图。
1 预备引理
引理1 设 G是一个图,g和f是定义在V(G)上的两个整值函数,且 g<f,若对任意的 x,y∈V(G),且 x≠y,有 f(x)dG(y)≥dG(x)g(y),则 G有(g,f)-因子。
引理2 设 G是一个图,g和f是定义在V(G)上的两个整值函数,且 g<f,则图 G是一个(g,f)-3 -消去图,当且仅当对V(G)的所有不交子集S和T有

其中ε(S,T)定义如下

2 主要定理及其证明
定理 设G是一个图,g和f是定义在V(G)上的两个整值函数,且1≤g<f-1,若对任意的 x,y∈V (G),有 f(x)≤dG(x)且 f(x)(dG(y)-3)≥dG(x)g(y),则 G是(g,f)-3-消去图。
证明 对V(G)的所有不交子集S和T,由引理2证明(1)式成立。当S≠ø时,由假设,对任意的x,y∈V(G)有 f(x)(dG(y)-3)≥dG(x)g(y),因此

这样

即

情形1 若G[T]中至少有3条边,这时必有|T|≥3,且

即 dG-S(T)≥6,于是

情形2 若 G[T]中只有2条边,且eG(T,V(G)(S∪T))≥1,此时必有|T|≥3且

即 dG-S(T)≥5,于是
dG(S)δG(S,T)≥5(dG(S)-f(S))+9 f(S)≥5 dG(S),所以δG(S,T)≥5。
此时|T|≥2且

即 dG-S(T)≥4,于是

所以δG(S,T)≥4。
此时|T|≥2,且

即 dG-S(T)≥3,于是
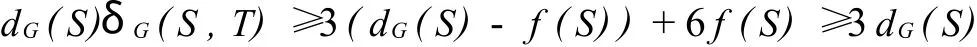
所以δG(S,T)≥3。
此时|T|≥2,且

即 dG-S(T)≥2,于是
dG(S)δG(S,T)≥2(dG(S)-f(S))+6 f(S)≥2 dG(S)
所以δg(S,T)≥2。
情形6 若上述5种情况都不满足,且 G[T]中没有边,且eG(T,V(G)(S∪T))=1
此时|T|≥1,且

即 dG-S(T)≥1,于是

所以δG(S,T)≥1。
情形7 若上述6种情形都不满足,此时|T|≥0,且

即 dG-S(T)≥0,于是

所以δG(S,T)≥0。这样,在S≠ø时证明了δG(S,T)≥ε(S,T)成立。
当S≠ø时,δG(S,T)=dG(T)-g(T)≥2|T|≥ε(S,T)。
综上所述,对V(G)的所有不交子集S和 T,证明了(1)式成立,从而由引理知图G是(g,f)-3-消去图。定理证毕。
[1]Lovasz L.Subgraphs w ith p rescribed valencies[J].Comb Theory,1970,8(2):391-416.
[2]Hoinrich K,Hell P,Kirkpartriok D G,et al.A simp le existence criterion for(g<f)-factors[J].Discrete Mathematics, 1990,85(1):315-317.
[3]Liu G Z.On(g,f)-covered graphs[J].Acta Math Scientia,1988,8(2):181-184.
[4]Liu G Z.(g<f)-facto rsof graphs[J].Acta Math Scientia,1994,14(3):285-290.
[5]Liu G Z.(g,f)-factors and(g,f)-factorizationsof graphs[J].Acta Math Scientia,1994,37(2):230-236.
[6]周思中.关于(g,f)-2-覆盖图和(g,f)-2-消去图[J].兰州大学学报:自然科学版,2005,41(6):106-109.
