应急系统中多资源多目标优化模型研究*
2011-12-08王兆玲
王兆玲
(潍坊学院,山东 潍坊 261061)
0 引言
众所周知,时间紧迫性是应急问题的一个最显著的特性,决策者需要在最短的时间内完成应急救援方案和资源调度决策。但是,由于参与应急的出救点数目会直接影响方案的可靠性以及会产生额外费用,因而出救点数目也应是值得重视的因素,在很多情况下,系统的稳定性和费用都相当重要。因而,这类问题的本质是一个多目标的优化问题。
目前,国内外学者对应急问题单资源情况下“应急开始时间最早条件下,出救点数目最少”的两阶段优化模型以及“时间最短,出救点数目最少”的多目标问题的研究已经有了一些较好的结果[1-5]。但实际过程中,许多情况下都不可避免的涉及多资源问题,而对多资源情况下考虑“时间最短,出救点数目最少”的多目标问题,至今未见简便的解决办法。本研究将对之进行深入讨论。
1 模型描述
设 A1,A2,…,An为n个应急物资供应点(可出救点),A为应急地点,x=(x1,x2,…,xw)为应急物资需求(向)量,xj表示对j种资源的需求量j=1,2,…,ω,Ai到A需要的时间为ti(>0),不妨设t1≤t2≤…≤tn,T(>0)为应急限制期,要求给出一方案(确定参与应急的出救点及各自提供的应急资源数量)在满足约束条件下,使得应急开始时间最早,出救点数目最少。
j=1,2,…,n;i=1,2,…,ω。xij表示Aj的第i种资源可用量;xij′表示采用方案φ时Aj参与应急的第i种资源可用量。可以看出,第j列表示出救点Aj参与应急的资源向量;第i行表示各出救点参与应急的第i种资源数量。
用 T(φ)表示最早应急时间,用 N(φ)表示出救点数目,并让Ҳ表示所有方案的集合,于是问题变为

2 模型分析与求解
定义1 如果不存在另一方案φ′,使得 T(φ)≥Tφ′N(φ)≥N(φ′),并且有一个不等式严格成立,则称方案φ是非劣的。
定义2 非劣方案φ对应的目标值[T(φ),N(φ)],称为非劣目标值;所存可能非劣目标值的范围,称为非劣目标值域。
算法思想:
由于应急问题中,对每种资源的需求程度不同,所以可利用层次分析法,专家打分法等给出每种资源相对应的权重,分别记为:α1,α2,…,αω。容易看出,最早应急时间 T(φ)与出救点数目 N(φ)是相互矛盾的目标。由于 T(φ)最多不超过 n中可能的选择{tn,tn-1,…,t1},让 T(φ)从大到小取值(φ为变量),N(φ)关于φ是递减的。这种现象的直观解释是如果一个非劣方案φ′,T(φ′)=ti,那么对任意一个在“时间”优于它的方案φ″,即 T(φ″)<ti,一定满足 N(φ″)≥N(φ′)。因为 T(φ′)∈{tn,tn-1,…,t1},让 T(φ)取遍所有可能的值,对 N(φ)做优化,即求解这样一系列的优化问题:

定理 根据(2)求出的一系列方案φi,i=1,2,…,v,其对应的目标值[Tφi,Nφi],i=1,2,…,v,构成的集合(平面上的点集,记为 F)一定包含非劣目标值域。
算法步骤:
记 X=(X1,X2,…,XN),α=(α1,α2,…,αω)则 X=αφ
(1)j=n,v=0

(3)j=j=1;
(4)若tj=tj+1,转步骤(3),否则转步骤(2)
(5)v=0时无解;否则用步骤(2)求解
如果决策者本身能给出他们的偏好函数即效用函数,那么只需对n个偏好函数值进行比较以确定最优方案。设 g(y,z)表示效用函数,y表示 T(φ),z表示N(φ),g是关于y,z的严格减函数。可以用下式求解多目标的最优解φ*:
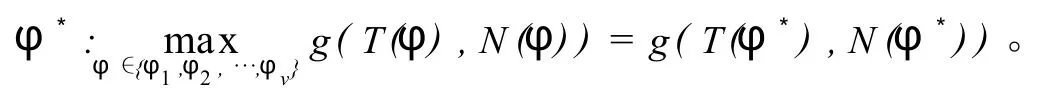
3 算例(以两种资源为例,数据见表1,计算过程见表2、表3)

效用函数


表1 数据(该数据来自某市的一次火灾救援)

表2 计算过程1

表3 计算过程2
结果及分析:对于效用函数(3),多目标问题的最优方案为φ1(即选择A6A7A8A9作为出救点)。在对公安消防支队的操作过程进行深入调研后,针对消防支队只是根据预警级别,盲目动用人力、物力;没有统筹规划,不能把资源合理利用到最大化等问题,笔者提出了上述模型及求解方法,该问题的结果得到了消防支队的认可。在上例中,当时公安消防支队出动了周边八个出救点进行救援,10分钟后,火势得到了有效控制。而从笔者计算的结果看,只出动四个出救点,就能满足灭火的需要,大大节省了人力、物力。
4 结束语
本文给出了多资源、多目标应急问题的数学模型,笔者以单资源的研究为基础,将多资源的情形通过加权转化为单资源的情形来解决,使得该问题简便易行。最主要的是该算法现经一年的试验运行,取得了令人满意的结果。而对需求和时间为模糊情况的运输问题更具有实际意义,这种情况下的应急问题是否也存在比较好的算法将成为该领域有待完成的工作。
[1]Tzeng G H,Cheng H J,Huang T D.M ulti-objective op tinal p lannting for designing relief delivery systems[J].Transpotrtation Research Part E:Logistics and Transpo rtation Review,2007,43(6):673-686.
[2]Shen J B.An emergency logistics distribution app roach fo r quick response to urgent relief dem and in disasters[J].Transpo rtation Research Part E:Lgistics and Transpo rtation Review,2007,43(6):687-709.
[3]Renaud J.A tabu search heuristic for the multi-depot vehicle routing p roblem[J].Computers&Operations Research, 1996,23(3):229-235.
[4]Tufekei S,Wallace W A.The emerging area of emergency management and engineering[J].IEEE Transactions on Engineering M anagement,2001,45(2):141-152.
[5]Andersen H B.MM S:an electroniemessagemanagement system for emergency response[J].IEEE Transactionson Engineering Managemnet,2005,45(2):132-140.
