金堤河范县水文站控制流域年降水中长期预报方案的研制
2011-12-08胡凤启
胡凤启
(开封水文水资源勘测局,河南 开封 475001)
0 引言
金堤河是黄河下游左岸一条支流,为平原河道,发源于河南省新乡县境,流经河南省新乡、鹤壁、安阳、濮阳和山东省聊城5 地市的12 个县,在河南省台前县张庄汇入黄河,干流河道长158.6 km,流域面积5047 km2。 由于金堤河流域情况的复杂性,洪涝灾害时常发生,为了更好地为防汛抗旱部门决策提供水文信息,减少对社会发展和人民生命财产的危害, 需要在较长预见期内对雨水情信息进行预报。 本文试对该流域年降水中长期预报方案进行研制。
1 流域概况
1.1 流域的地形地势
金堤河流域南临黄河大堤,北界卫河、马颊河、徒骇河,西起人民胜利渠灌区,呈狭长三角形,上宽下窄,东西长200 km,南北最大宽度60 km,平均宽度25.5 km。 流域地势西南高、东北低,从河源至河口高差为30 m,比降平缓,一般在1/6 000~1/15 000之间。流域内坡洼较多,河道宽浅,排水不畅。其中,范县站以上坡洼主要有大沙河、道滑坡、宋庄坡、白马坡、金堤二节及卫南坡等,流域面积4 704 km2。
1.2 流域的气象条件
金堤河流域属温带季风气候区,夏季受西太平洋副热带高压控制,水汽充沛,冷热气团交替,多锋面雨和气旋雨,雨量多且集中;冬季和春季受西伯利亚冷高压控制,雨雪稀少,风多干冷,空气干燥,蒸发量大。 该地年平均气温13.7℃,最高42.6℃,最低-19.9℃,无霜期210 d,光照充足,全年日照时数达2 500~2 600 h。 流域多年平均降雨量606.4 mm,降雨年际变化较大,年内分配不均,汛期6~9 月,受夏季东南风影响,雨量较多,降雨量约400 mm,占年降雨量的70%左右,冬春缺雨雪,旱涝交替频繁出现。 流域多年平均蒸发量为1 109 mm (E601 蒸发皿),干旱持续时间较长,蒸发量年际变化不大,年内变化大,最大月蒸发量多出现在5~6 月份。
2 资料来源及处理
2.1 资料来源
本次年降水长期预报模型研制依据的基本资料为:H500 mb (20N、70、80、90E)3 点高度,H500 mb(50-55N、70-90E+40-45N+65-85E) 巴尔喀什湖区一等22 个气象因子1955~1999 年共45 年的资料,河南省金堤河流域范县站以上1956~2000 年年面降水资料(由该区域马楼、龙王庄、范县、徐镇、濮城、濮阳和王辛庄7 个雨量站面积加权求得)。
2.2 资料处理
根据预报因子和对象的系列情况,选取1955~1994 年各气象因子的逐月资料,并与1956~1995 年对象资料相对应建立Excel 表格,以便用Excel 软件数据分析选项卡中的相关系数功能挑选因子, 用回归功能计算,作回归分析,进而建立预报模型。 对1995~1999 年因子资料和1996~2000 年对象资料(均为5 年)进行实际预报和检验。
3 计算原理和检验方法
3.1 计算原理.
本次模型研制采用22 个预报因子 (1955~1994年) 逐月资料与预报对象——金堤河流域范县站以上年降水(1956~1995 年)进行线性回归分析[1]。 用多元回归方法建立预报模型,并对模型进行了精度评定。 最后,用1996~2000 年的实测资料,对预报模型进行可信度检验。
多元回归分析是把已挑选出来的预报因子一次引入,建立回归模型。 若预报对象为Y,已挑选出m 个前期预报因子为X1,X2, … ,Xm, 则回归模型为:
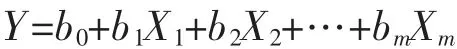
按最小二乘法原理,用一般的高斯消去法确定回归系数后,就可确定回归方程。
3.2 检验方法
为了判断多元回归分析和逐步回归分析得到的回归方程的回归效果,采用F 检验,即
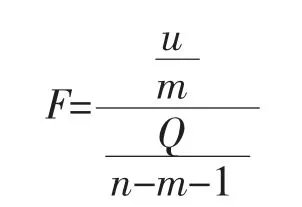
回归效果的F 检验,即检验全部自变量的回归系数与0 有无显著差异。 当差别显著时,说明回归方程中的预报因子是起作用的。 当全部与0 无差别(即bi全为0 的假设成立)时,由回归方程计算出来的Y 在任何情况下都恒为一个不等于b0的常数,则回归方程就没有任何意义。 由统计量F 可以看出,F越大,则回归效果愈好。 检验时,根据确定的信度α,在F 分布表中,根据自由度m 与n-m-1 查出相应的Fα。 当计算出的F>Fα, 说明回归效果显著,若F<Fα,则回归效果不显著。
4 预报模型的建立
4.1 挑选预报因子
本次挑选预报因子是对22 个预报因子的逐月系列(共22×12 个)和预报对象(金堤河流域范县站以上年降水)系列分别计算单相关系数[2],按照与对象相关系数大于0.3 的标准,选取8 个相关最好的因子(0107、0310、0705、0901、1501、1503、1601、2107,因子0107 表示01 号因子7 月份系列,其他依此类推)作为初选因子。 为了保证因子之间的独立性,对初选的8 个因子求自相关。 如果某两个或两个以上的因子相关性较好(相关系数大于0.4),则选取其中与预报对象相关最好的一个因子作为这几个因子的优选因子,而剔除其余因子。 按照这个原则,最终选定4 个因子(0705、1501、1503、2107)进行回归分析计算。
4.2 建立模型
在挑选出的前期预报因子的基础上,根据1955~1994 年4 个前期预报因子和1956~1995 年金堤河范县站以上流域年降水量,进行回归分析(用Excel软件的回归功能计算)。 经计算,得F 检验值为8.540 698,选取信度α=0.05,查表得Fa=2.606,F>Fa,则回归方程效果显著。故建立预报方程(预见期为1年)为
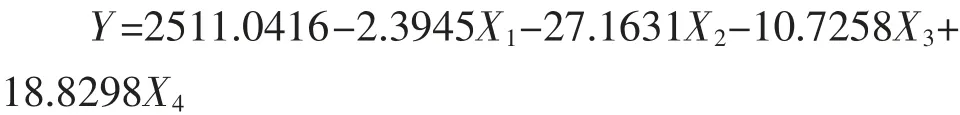
式中:X1为因子7/5,上一年的“H500mb (25-35N、110-130E) 长江中下游区7 点合计”5 月份的值;X2为因子15/1,上一年的“西风风速V37.5m/s,(105E、35-40N)”1 月份的值;X3为因子15/3, 上一年的“西风风速V37.5N(m/s)(105E、35-40N)”3 月份的值;X4为因子21/7,上一年的“C102 、102 站西风指数(115E、25-30N)”7 月份的值。
5 结果分析
5.1 拟合精度分析
根据已建立的预报方程,用1955~1994 年的预报因子对1956~1995 年预报对象的值进行预报,经计算,得金堤河流域范县站以上年降水预报模型历年拟合误差。 根据 《水文情报预报规范》(SL250-2000)[3]的要求,对本长期预报回归模型作精度评定及实际预报精度评定。 评定是否合格的许可误差为与实测数值相差小于20%。 从拟合误差看,40 年中有12 年的误差超过了20%,有28 年的误差在20%以下,合格率70%,满足系列长70%的要求,故可进行预报。 实测值与预报值的历史拟合状况如图1 所示。
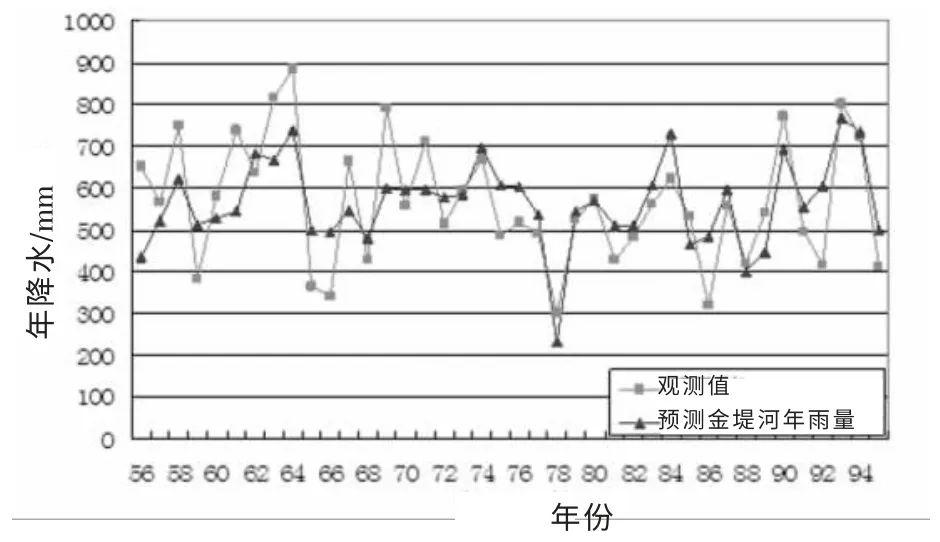
图1 金堤河流域范县站以上年降水实测值与预报值历史拟合图Fig.1 Historical fitting chart of annual rainfall measured values and annual rainfall forecasting values above Fan county station of Jindi River basin
从图1 可以看出,所建立的预报模型的预测数据与实测数据拟合情况比较好, 有一定的预报精度,一些误差较大的年份大多是丰水和枯水年份。 可见,多元回归建立起来的模型在预报异常年份时还存在一些问题。 这是因为多元回归仅考虑了预报对象与预报因子间的线性关系,而没有考虑相互间的非线性变化。 因此,一些特殊年份的预报结果就不是很理想。 另外,一些年份误差较大,也可能是受到人类活动和实测值精度等因素的影响。
5.2 预报结果分析
本次用预报模型对1996~2000 年金堤河流域范县站以上年降水进行预报,作为对模型的预报检验,预报值和预报误差如表1 所示。 从预报结果看,1996 年误差为33%,其余4 年误差均在20%以下,预报准确度达80%,说明该预报模型良好。
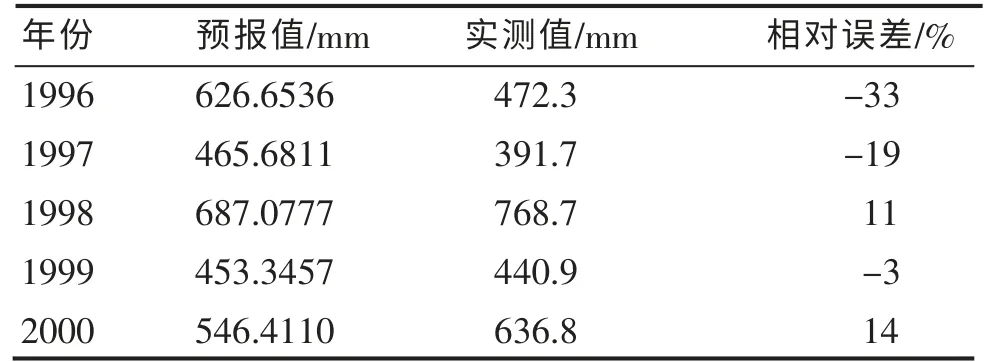
表1 金堤河流域范县站以上年降水预报及误差评定表Table 1 Annual rainfall forecasting values and error evaluation above Fan county station of Jindi River basin
6 结语
(1)通过拟合检验和预报检验可以看出,本文所建立的金堤河范县站以上流域年降水量预报模型基本满足要求。
(2)多元回归在预报因子重要性和独立性上未作考虑。 它不论m 个因子对预报对象是否同样重要,一次就将所有因子引入,没有分析它们与预报对象的主次关系。
(3)线形回归分析所作出的预报估计值是在样本容量一定、各个预报因子取某一数值的条件下预报对象可能出现的条件平均值。 因此,所得预报估计值是比较折中的,难以报出异常情况。
(4)回归方程是根据历史资料选配的,对实测资料超出历史范围的年份, 预报值会有一定的误差。所以,应尽可能增大样本资料,即增加分析资料的年限,作进一步分析。
(5)本次预报模型为初步研制,所采用的预报因子为一般性的22 种因子。 如果选取适当方法,找到一些物理成因与预报对象更密切的因子建立模型,将会进一步提高模型的拟合精度及实际预报精度。
[1] 黄振平. 水文统计原理[M]. 南京:河海大学出版社,2002:205-212.
[2] 毛昭雄.中长期水文预报[M].南京:河海大学出版社,2004:29-30.
[3] SL 250-2000,水文情报预报规范[S].
