单股水平淹没射流的理论计算与数值模拟

高永辉，王新建

（商丘师范学院 建筑与土木工程系，河南 商丘 476000）

0 引言

射流按不同的流态、喷口形状、环境固体边界，以及射流原动力等，可分为不同的类型[1]：按流动形态可分为层流射流和紊流射流（高速冲击射流为紊动射流）；按射流的物理性质，可分为不可压缩射流和可压缩射流、等密度射流和变密度射流。 从环境的性质来划分，射入同种性质的流体内的射流称为淹没射流，射入不同性质的流体内的射流称为非淹没射流[2]。

1 理论分析

取单宽水流进行分析，设射流入水断面为均匀掺气[3]。 浓度为β0、断面平均流速为u0、掺气射流厚度、纯水当量厚度d0=E(1-β0)。

掺气射流的水下扩散中心线位置最大流速计算如下

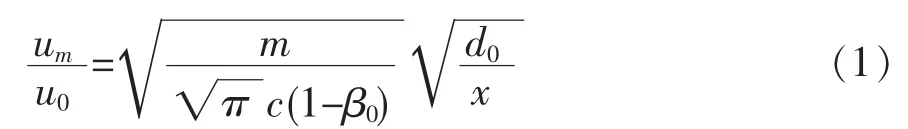
当射流为纯水时， β0＝0，式中系数c、m 需由试验确定。

1982 年，余常绍已经对垂直纯水流的扩散进行了试验研究[4]，得出射流中心轴线上的速度变化规律（如式（2）所示）：

式中：u0为射流入水流速，m/s；um为射流轴线流速，m/s；b0为射流入水宽度，m；S 为流程，m。

式（2）表明，u0/um与流程S 呈直线关系。 采用该式计算单股水平淹没射流轴线的最大流速。 为使计算结果和FLUENT 模拟结果有更充分的比较，将在射流入水宽度b0＝0.5m 时，取入射水流流速u0＝10m/s，流程S＝1m、3m、5m 的情况下，计算射流轴线流速um的取值，计算结果见表1。

表1 射流轴线流速随流程变化值Table 1 Values for jet axis flow rate changing with flow

由表1 可以看到，射流轴线流速um随流程S 呈直线变化，并随S 的增大而不断变小。 这说明，伴随着流程S 的不断增大，射流轴线流速um能量的耗散也越来越大。

2 FLUENT 模拟分析

2.1 边界条件的设定

在FLUENT 计算中，把边界条件定义为进口边界和出口边界， 其中进口边界包括： 速度进口u0＝10m/s，水力直径DH＝0.5m。 把流体进口边界设定为速度入口。 相应的入口紊动能和耗散率的边界条件可由下列经验公式得出[5]：

式中：U0为进口流速，m/s；H0为进口水深，m。

由于出口边界为自然溢流，与大气相通，故可以认为出口压力为大气压力值， 即一个大气压（10135Pa），所有变量的法向梯度为零。 出口水力直径可由式（5）求得（DH＝3.755m）。

式中：DH为出口水力直径，m；L 为池长，m；W为池宽，m。

2.2 入射水流流速u0＝10m/s

射流入水宽度b0＝0.5m，入射水流流速u0＝10m/s，流程S＝1m、3m、5m 时，射流轴线流速um的取值。模拟结果如图1～3 和表2 所示。

为了充分对比理论计算结果，把沿射流轴线平面流程S＝1m、3m、5m 时的纵切面，分别记做平面1、平面3 和平面5，平面内的流速分布及流速值如图1～3 所示。 流速分布图中速度等值线中的数值或颜色代表所在点的流速，流速散点图中深色散点代表横面流速，浅色散点代表纵面流速。

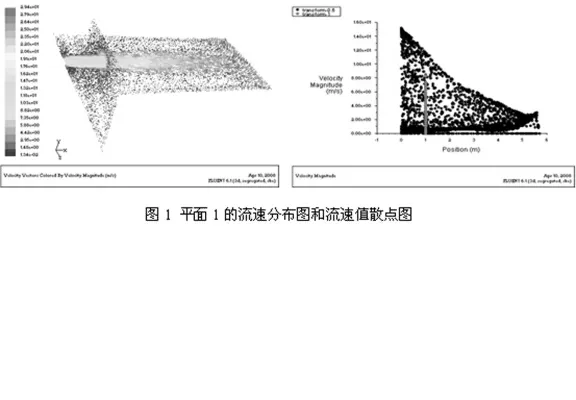
图1 平面1 的流通分布图和流速值散点图Fig.1 Circulation distribution and velocity values of plane 1

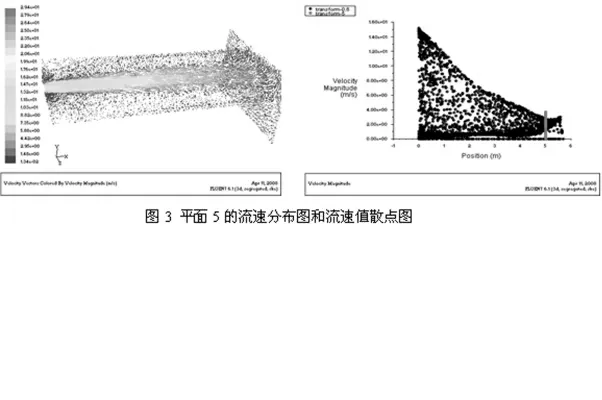
图2 平面3 的流通分布图和流速值散点图Fig.2 Circulation distribution and velocity values of plane 3

图3 平面5 的流通分布图和流速值散点图Fig.3 Circulation distribution and velocity values of plane 5

表2 射流轴线流速在沿轴线纵平面上的最大值Table 2 Maximum value of jet axis flow rate along the axis on vertical plane

以上研究结果显示，当入射水流流速u0＝10m/s、流程S＝1m 时，射流在进入消能池后扩散不充分，流速难以降低，中心轴线流速依然非常大，高速射流能量几乎没有产生太大的损耗， 流速分布非常密集。 在流速散点图上可以清晰地显示，其中心轴线处的流速达到9.4m/s。 流程S＝2m 时， 流速有所减弱，能量也有所耗散，流速值散点图示出，此时最大流速为8m/s。 随着流程的不断增大，射流在进入消能池后扩散越来越明显，能量耗散也越来越大。 当流程S＝4m 时， 在平面4 上的中心轴线最大流速分别降低为5.9m/s。 当流程S＝5m 时，扩散最为充分，消能效果最为明显， 高速射流的能量耗散也最大。此时射流在平面5 上的流速也最小。只有4.1m/s，对消能池各壁面的压力才降到最低值，破坏程度降到最小。

3 分析比较

由理论计算结果和FLUENT 数值模拟结果比较显示， u0＝10m/s 两种计算结果基本吻合 （如表3和图4 所示）。

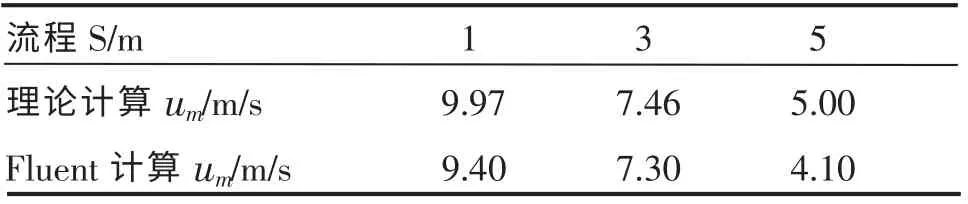
表3 两种计算方法数据比较Table 3 Data comparison of two kinds of calculation methods

4 结论

理论计算与现实情况存在差异， 当采用FLUENT 计算模拟时，消力池内水体紊动剧烈，流速最大值的出现位置和大小并不固定，且较难确定其准确位置和方向，故与理想的理论分析结果有微小的偏差。 因此，在进行较为复杂的淹没射流流速、压力数值计算时， 完全可以用CFD 数值模拟的方法，对消能池内的流速场、压力场进行模拟分析。 这样即可大大减少工作量，又可相对真实地反映消能池内各个点、面的流速及压力分布。

[1] 台尔曼. 消力池中消力墩的作用[J]. 水力发电，1957（12）:17-20.

[2] 陈永灿,许协庆. 射流对下游河床冲击作用的数值模拟[J].水动力学研究与进展，1992（3）：52-55.

[3] 刘沛清. 挑射水流对岩石河床的冲刷机理研究[D]. 北京：清华大学博士学位论文，1994:37-38.

[4] 韩占中，王敬，兰小平. FLUENT-流体工程仿真计算实例与应用[M]. 北京：北京理工大学出版社，2004:102-131.

[5] 吴子牛. 计算流体力学基本原理[M].北京：科学出版社，2001:127-129.