一种基于统计模型和时序分析的弹痕比对方法
2011-12-08贺力克周华祥
贺力克,周华祥
(湖南工业职业技术学院,中国长沙 410208)
一种基于统计模型和时序分析的弹痕比对方法
贺力克*,周华祥
(湖南工业职业技术学院,中国长沙 410208)
提出了一种枪弹头弹痕自动比对方法.首先通过常规的采集设备采集弹痕数据,通过对弹头实际测量数据的统计建模,利用概率模型构造出一个代价函数,当该代价函数的取最小值时,即可估计出平移误差和转动误差,从而有效的消除了测量数据中的各种误差.通过时间序列分析比较两个弹痕的相似程度,结果表明该方法在可接受的计算时间内有效地解决了弹头痕迹的自动比对问题,精度和效率都较传统方法有显著提高.
弹痕检测;比对方法;统计分析;时间序列分析
枪弹痕迹检验是用来侦破涉枪案件的一项重要的刑侦技术手段[1].由于制造、使用、保管等方面的原因,不可能有两支膛线完全相同的枪,枪弹痕迹检验的主要任务便是枪支的同一认定,也就是要确定现场弹头、弹壳是哪一支枪发射的.因此,枪弹痕迹鉴定和指纹鉴定、DNA鉴定一样,都是枪械性能分析与枪案刑侦工作中不可或缺的部分[2].传统的子弹比对方法,如比对显微镜检测法、分段照相、触针检测[3]等方法,有着无法获取三维信息、精度不高、影响物证物理完整性、无法进行计算机自动比对的缺陷[4].随着现代高精度数据测量、采集设备和信息技术的发展,为弹痕的自动化比对创造了必要条件[5].
自动化比对过程一般可以分为两步∶首先用光学设备采集弹头上弹痕的3维数据[6] ;然后用计算机软件根据一定的模型判断子弹间的相似程度,确认发射子弹的枪支[7].我们一般着重研究第二步,在获取了样本数据之后,如何采用有效的方法进行提取特征并验证同一性.为此,学者们做了很多基础的研究.由于弹痕采样的方法有不同,对于弹痕数据的处理也各有特点.
对于图像方法而言[5],系统首先通过视频显微仪采集弹痕图像,处理后提取细节特征,然后将这些细节特征与保存在数据库中模板细节特征进行匹配,判断输入细节特征与模板细节特征是否来自同一支枪支发射的弹痕.周鸣争[8],张树江[9]及权贵秦[10]等人做了这方面的研究.曾文涵等人提出了基于小波分析技术的弹头表面纹理特征提取方法,对于传统小波分析的边界失真进行了深入的分析,对于提取弹头特征有着重要的意义[1],郭军等人提出了一种弹头发射痕迹计算机图像比对系统[11].曾文涵和郭军又对另一种采集信号的方法进行了深入的研究,设计了一套弹头发射痕迹计算机识别系统[7].由于该套系统采用的是机械测量的方法,与以往的数据处理方法有着很大的不同.
目前的文献中,只有[12]中对此做了一些研究,从纯粹数据处理的方面来考虑如何进行弹痕比对,利用小波去噪、相似度配准等方法对其进行了研究.
然而在光学设备上测量弹头上弹痕的3维数据时,需要人工调整弹头的位置和姿态.人工操作中必然会造成一定的误差,文献[12]只是用小波去噪的方法只能消除一部分噪声,而如何处理弹头姿态位置造成的误差并没有进行讨论.本文深入研究了如何使得两个弹头可以尽量在相同位置和相同姿态的情况下进行比对这个首要问题,接着讨论了如何消除随机误差对测量结果和比对结果的影响,最后设计了一套完整的弹头比对模型和算法.
1 枪弹头弹痕比对问题建模
1.1 弹痕比对问题描述及建模
枪弹发射后,弹头上留下了枪管膛线的擦痕痕迹.枪管有4条凸膛线共8个棱,分为4个主棱和4个次棱,所以在弹头上留下的痕迹分为4片主棱线的痕迹和4片次棱线的痕迹.图1所示为子弹头表面的次棱痕迹,可以看出由于枪弹通过枪管时只旋转了一个很小的角度,擦痕分布成斜线状(与圆柱母线有一个夹角),每一片痕迹的主要部分都显示为不同大小和不同深浅的线条[6].高精度数据采集设备采集弹头上8片痕迹的3维数据,测量的基准平面取为固定在测量设备上的空间直角内.
通过上述对弹痕比对问题的描述,建立如下模型.设空间直角坐标系xoy平面,测量设备可以测得数据为弹头表面上每一个点的空间坐标(x,y,z),且沿x轴方向和沿y轴方向的测量步长为τx和τy,z的测量精度为τz.子弹头的直径为d,长度为l.模型如图2所示.

图1 子弹头表面弹痕的次棱
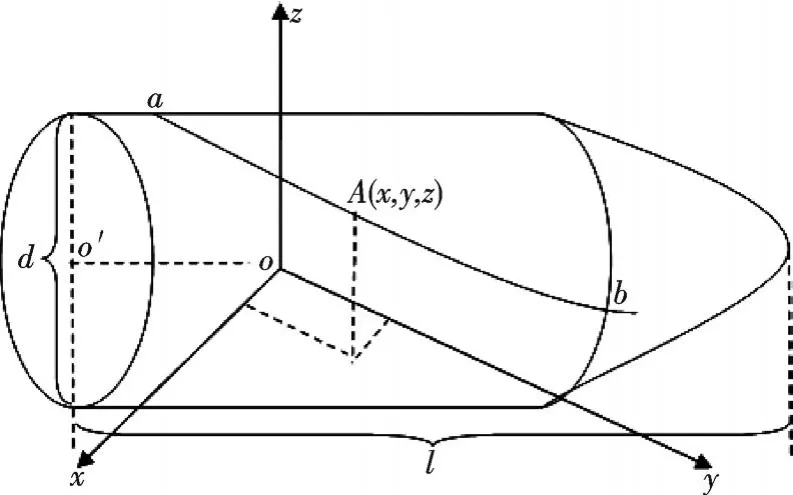
图2 子弹头弹痕表面建模
1.2 弹痕测量中的误差分析
通过对弹痕比对问题的建模分析可知,由于基准平面在弹头痕迹的附近,测量时调节弹头的姿态使得弹头圆柱中心线尽量平行于基准平面,且y轴尽量平行于擦痕的走向.由于弹头的姿态靠人工调节,所以上述的两个平行都不是准确的平行,造成了一定的测量误差.测量误差主要包括以下几个方面∶
(1)平移误差∶也可称为共轴误差(coaxiality error)[2],即测量坐标系的差异造成的测量误差.在空间直角坐标系xoy中,平移误差可以分解为x轴、y轴、z轴3个方向的误差.所以,消除平移误差也就是通过移动原有的测量坐标系,对测量值做线性变换,消除3个方向上的误差,使得参与比对的子弹的位置基本相同.因此假设x轴方向平移误差ξx,y轴方向平移误差ξy,z轴方向平移误差为ξz.
(2)转动误差∶即测量中由于人工调节,造成子弹的姿态不同所带来的测量误差.因此,消除转动误差,就是要使参与比对的弹头的姿态尽可能的相同.故设子弹头转动的误差为ζ.
(3)测量精度是每次测量中都必定包含的第三类误差源,在此假设第i次的测量误差用εi表示.
通过3种造成测量误差的主要因素的分析,可知,在比对过程中最重要的是要消除平移误差和转动误差对比对结果造成的不利影响.要进行弹痕比对必须将弹头精确的摆放在相同位置,而通过坐标变换精确的将两个弹头变换到同一坐标系的同一测量位置是不可能的.
2 基于概率分布的误差消除方法
子弹的一系列测量数据可以看作是在重复测量某一物理量X,获得的一系列容量为n测量数据样本(x1,x2,…,xn).设X的精确值为x,第i次测量值为xi (i=1,2,…,n),则误差εi为∶

设εi的概率密度函数为f(xi -x),由εi (i=1,2,…,n)的相互独立性可知ε1,ε2,…,εn的联合概率密度L为∶

由极大似然估计法可知,L越大,x1,x2,…,xn越能表现出真实情况[13].故令∶

而又有L与lnL在相同点x处取得极大值,下式成立∶


即εi~N(μ=0,σ2).
对于平移误差ξ,满足ξ~N(μ=0,σ2).若假设测量误差以0.99的置信度在置信区间[-0.03,0.03]内,则其概率密度函数为∶

因此x轴、y轴、z轴上的误差变量ξx,ξy,ξz均服从ξ~N(0,0.0132),概率密度函数同样可以一一求出,这里就不再赘述.而对于转动误差ζ,同样也服从均值为0的正态分布,且以0.99的置信度分布在[-0.2°,0.2°]之间,可求得σ=0.008,则有∶

可以认为,当小概率误差出现时,应该给予较大的惩罚.依据该原则,构造如下代价函数∶
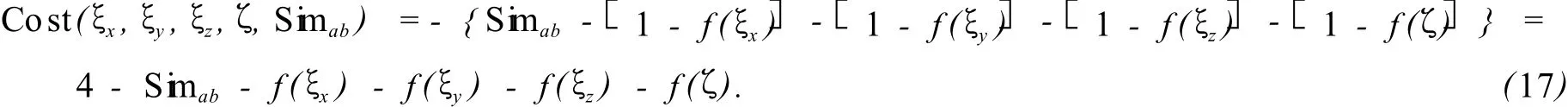
其中-0.03 mm≤ξx,ξy,ξz≤0.03 mm,-0.2°≤ζx≤0.2°.当在该约束条件下,求得代价函数的最小值时,即可估计出平移误差和转动误差.Simab表示a,b两个弹痕的相关度,可见该值不仅依赖于所比对的弹痕数据,也依赖于ξx,ξy,ξz,ζ.
3 基于时间序列的弹痕比对算法
从子弹测量数据中可以假定是在重复测量某一物理量a,获得了一系列测量数据x1,x2,…,xn (n=1,2,…,N).上述子弹的测量数据序列可以看成是按时间顺序取得的一系列观测值,因此可以将x1,x2,…,xn序列看作是一个时间序列.x1,…,xn时间序列共有n个观测值,将其组成(n-1)对数据,如(x1,x2), (x2,x3)…(xt,xt+1)…,(xn-1,xn)[14].根据两变量相关系数的概念,我们可以计算出上述(n-1)对数据的相关系数ρ,则有∶

其中

则称ρ1为时间序列的自相关系数,它与两变量的相关系数含义不同.它是用来度量时间序列上一次的测量数据和下一次的测量数据之间的关系,从定量的角度来研究上一次观测值对下一次观测值的影响程度有多大.
我们选择了弹痕数据的相关系数来定义弹痕之间的相似度.即∶

相关度定义如下∶设两次测量中,z轴的测量值集合分别为a1,a2,…,an和b1,b2,…,bn,则两列变量的相关系数Corr(a,b)为∶

在弹头匹配的过程中,根据基本假设,可认为无论是否由同一支枪发射,弹头之间的相似度都是很高的,那些少部分的差异才是区分弹头来源的信息.所以,基本的思路就是在进行空间平移和转动消除测量误差时,对每种情况都尝试4种可能的次棱配对方案,选取其中匹配得最好的两对次棱的相关系数的和的最大值作为两个弹头的相似度,具体步骤如下∶
(1)对弹头的测量数据进行采样和截取,获得有效的、规模较小的、可用于比对的数据.
(2)在一定的范围内搜索x轴、y轴、z轴3个方向上的平移误差ξx,ξy,ξz和转动误差ζ的最优值,使得代价函数Cost(ξx,ξy,ξz,ζ,Simab)最小.在[-|ξx |,|ξx |]之间的每个ξx,ξy,ξz和[-|ζ|,|ζ|]之间的每个ζ的组合,计算4种次棱对应关系情况下的相似度(相似度的计算稍后介绍)最高的两对次棱之间的相似度的和,此即为两个弹头在当前误差情况下的Simab.从而计算出Cost(ξx,ξy,ξz,ζ,Simab).
(3)找到Cost(ξx,ξy,ξz,ζ,Simab)的最小值,以及每两个子弹的次棱对应关系和相似度,并输出结果.
4 基于时间序列的弹痕比对算法
本文的试验数据采集自某次对弹头痕迹的测量结果,由于数据量过大,参见文献[15].试验过程中的基本参数和弹头的原始数据值如表1所示.
图3为某段含有严重噪声误差的测量值曲线,图4为其三维还原图,可以看出弹头的某些部分有明显的损毁情况.并不是所有的数据都可以用于比对,尤其是在数据开头的部分,由于弹头受到外部冲击或是其他破损,数据中有大量的不可用于比对的部分.经过我们的算法处理之后,含有误差噪声的测量值曲线已经经过处理,可以较好的用于弹痕比对,消除结果如图5和图6所示.

表1 弹痕比对算法的参数设定
采用上述算法对文献[15]中的4组弹头测量数据M与其他8个待比对样本T进行模型的测试和验证,进行次棱对比都取得了较好的效果.结果如表2所示,表中粗体表示通过对比模型求得的与待测样本相似度最高和次高的值,双线框表示真实结果.可以看出,我们提出的比对算法具有很高的识别率,也能给出最优的估计值.例如M1与T3、T7弹头相似度较高,且与T3最高,比对正确;M2与T4和T7弹头相似度较高,且与T4最高,比对正确;M3与T2和T5弹头相似度较高,且与T5最高,比对正确;M4与T6和T7弹头相似度较高,且与T6最高,比对正确.

图3 某段含有误差噪声的测量数据

图4 含有噪声的弹痕三维还原图
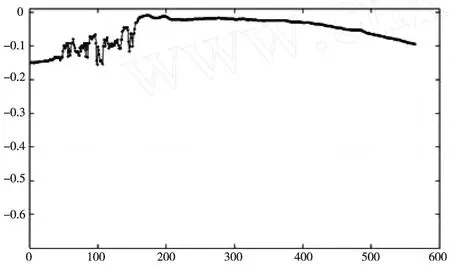
图5 消除误差噪声后的测量数据

图6 消除噪声后的弹痕三维还原图
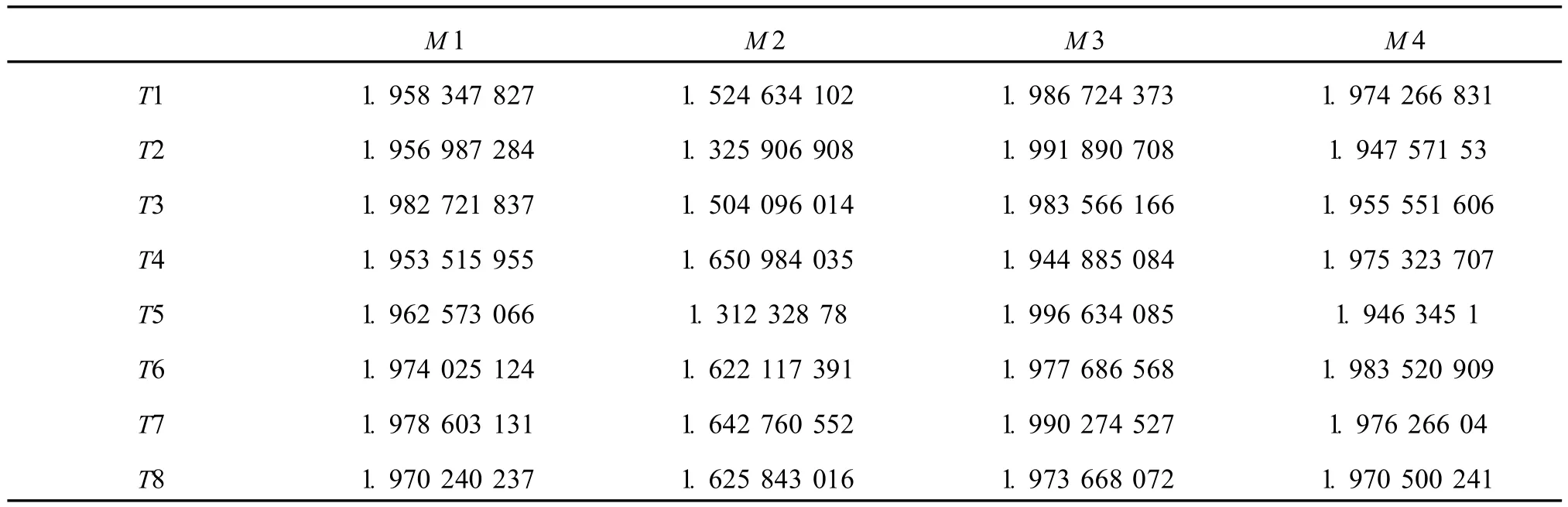
表2 弹头与待测样本的相似度列表及对比结果
5 结束语
本文中提出了一个基于统计模型的误差消除方法和基于时间序列分析的弹头比对算法,首先对弹痕数据进行统计建模,构造一个误差的代价函数,当该函数最小时,可以将弹痕采集过程中的误差消除,从而大大提高了比对过程的精度.
对弹痕数据进行处理之后,通过时间序列分析方法对待检测弹痕和样本弹痕进行相关棱匹配和相关系数检测,使用弹痕数据的相关系数来定义弹痕之间的相似度,从而分析弹痕的匹配程度.如果计算出的相似度较高,则可以判定是同一枪支射出的两枚子弹;反之,则不是同一枪支发射.由于在比对之前对弹痕数据进行了统计建模消除了部分的误差,因此在比对过程中置信度较高.实验结果表明,该方法对变形不严重的子弹弹痕检测有一定的实用价值.
[1] 曾文涵,杨练根,谢铁邦,等.弹头发射痕迹纹理特征提取方法的研究[J].仪器仪表学报,2001,22(1):203-204.
[2] 高 野.对射击弹壳上几种痕迹特征变化的分析[J].辽宁警专学报,2003,22(6):36-38.
[3] 蔡立红,健 卫.小口径运动步枪弹痕研究[J].广西公安管理干部学院学报,2001,50(1):36-37.
[4] 鲁 静,李德华,吴士泓.基于图像纹理分布的算法在子弹自动比对中的应用[J].武汉大学学报(理工版),2007,53 (5):543-547.
[5] 潘自勤.对枪弹弹头很急特征自动检索技术的探讨[J].警察技术,2003,6:29-31.
[6] 李 旦,杨练根,谢铁邦.弹头发射痕迹非接触三维检测仪[J].兵工学报,2003,24(3):347-350.
[7] 曾文涵,郭 军,谢铁邦.蒋向前弹头发射痕迹计算机识别系统的研制[J].华中科技大学学报(自然科学版),2002,30 (6):40-42.
[8] 周鸣争,汪 军.基于直方图变换的弹痕图像增强技术及实现[J].安徽机电学院学报,2002,17(4):31-33.
[9] 张树江,邢 慧,颜景龙.一种基于相似度的子弹识别方法[J].广西师范大学学报(自然科学版),2006,24(4):223-226.
[10] 权贵秦,安毓英,王凤琴.双参考面FTP法测量弹痕轮廓[J].西安电子科技大学学报(自然科学版),2007,34(5):805-808.
[11] 郭 军,曾文涵,谢铁邦.弹头发射痕迹计算机图像比对系统研究[J].兵工学报,2003,24(4):504-508.
[12] 吴海江,李一民,吴 伟,等.基于枪弹头痕迹自动比对方法的研究[C]//2009年研究生学术交流会通信与信息技术论文集.北京,2009:350-353.
[13] 罗健旭,常 青.软测量技术的数据预处理方法研究[J].控制工程,2006,13(4):298-300.
[14] 周 黔,等.基于重要点的时间序列趋势特征提取方法[J].浙江大学学报(工学版),2007,41(11):1782-1787.
[15] 2009年研究生数学建模竞赛B题[EB/OL].http://www.shumo.com/home/h tml/481.html,2010-09-23.
A BulletMark Comparison Method Based on StatisticalModel and T im e Series Analysis
HE L i-ke*,ZHOU Hua-xiang
(Hunan Industry Polytechnic College,Changsha 410208,China)
A bulletmark comparison method was proposed.Bulletmark data are gathered according to generally used equipment and a statisticsmodeling is set up to construct a cost function.Using this cost function moving error and rotation error can be estimated when the cost function getsmin imum value.Thismethod can eliminate all kinds of errors efficiently.The s imilarity of two bulletmarks is compared through time series data analysis.Results showed that thismethod can solve comparison problems of bulletmark in an acceptable computational time and its precision and efficiency are remarkably improved compared with traditionalmethod.
bulletmark detection;comparison method;statisticsmodeling;time series analysis
O434.19
A
1000-2537(2011)02-0030-07
2011-01-17
湖南省科技厅资助项目(2009GK3091);湖南省教育厅科研资助项目(09C1138)
*通讯作者,E-mail:HLK6666@126.com
(编辑 陈笑梅)
