基于冲突性判定的证据组合新方法＊

熊彦铭，杨战平

（中国工程物理研究院电子工程研究所，四川绵阳 621900）

0 引言

证据理论又称 Dempster－Shafer理论，是由Dempster和Shafer在概率论基础上发展起来的。证据理论比传统的概率论更好的把握了问题的未知性和不确定性，为不确定信息的表达与合成提供了一种有效的方法。

多传感器信息融合系统中，由于传感器性质、外部干扰或其它不确定因素的影响，使得从不同信息源获得的证据之间可能存在较大冲突。DS（Dempster－Schafer）组合规则在组合冲突证据时，有可能产生有悖常理的组合结果。因此，如何在证据冲突情况下实现多源信息的有效融合是证据理论的一个关键问题。文中分析了已有组合方法中存在的问题，提出一种新的证据组合方法。通过仿真实验与现有的几种主要方法进行比较，表明该方法简洁实用，能有效处理高度冲突的证据，得到合理的组合结果。

1 DS组合规则及其改进方法

1.1 DS组合规则存在的问题

证据组合规则是证据理论的核心内容，对组合结果正确与否起着关键作用。设m1和m2为辨识框架Θ上两个不同证据的Mass函数，则DS组合公式为：

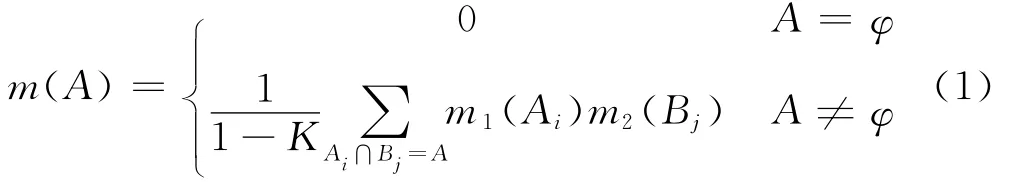
1.2 各种改进的证据组合方法

对DS组合规则的改进方法主要有两种策略，包括修改规则法和模型修正法。

1）修改规则法[1－5]：该类方法认为，DS规则在组合过程中完全丢弃了冲突信息。因此，修改规则法的主要出发点是研究如何将冲突进行重新分配的问题。修改规则法的代表是Lefevre[1]提出的统一信度函数组合方法，主要是解决两个问题：①冲突应该分配给哪些子集；②冲突应该以什么比例分配给这些子集。Lefevre的组合规则为：

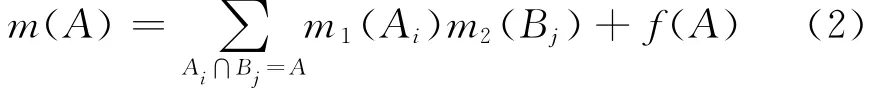
其中f（A）为证据冲突概率的分配函数，它满足：

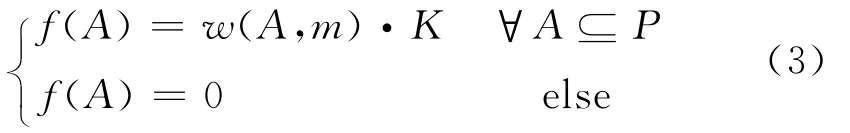
式中：P为冲突重新分配的子集集合，w（A，m）为证据m中命题A的权重因子。

统一信度函数组合方法的关键在于如何确定子集集合P和权重因子w（A，m），通过选择不同的P和w（A，m）可以引申为冲突分配法的其它方法，如Yager方法[2]、Smets方法[3]、孙全方法[4]等。

2）模型修正法[6－11]：Haenni[6]分析指出。从哲学的角度来看，“在模型x上使用方法y获得一个不符合直觉的结论z”时，Lefevre等人认为是方法y出现问题，而Haenni认为实际情况可能是模型x本身的问题，认为应该保持DS组合规则不变，通过模型修正，即调整原始证据的基本概率分配来解决冲突证据的组合问题。

文献[7]提出一种证据平均组合方法：对N条证据进行算术平均，将平均证据作为新的证据源，再利用DS组合规则进行（N－1）次组合。文献[8]对该方法进行了改进，为每一条证据赋予不同的权值，最后利用DS规则进行组合。证据平均组合法具有较快的收敛速度。但文献[9－10]分析指出，该方法用平均证据作为证据源，其合理性受到质疑。

文中主张用模型修正法来解决冲突证据的组合问题。通过引入DICE相似度[12－13]计算不同证据的可信度。利用可信度加权平均证据对各原始证据进行冲突性判定及修正，最后利用DS规则完成证据组合。仿真算例表明了本算法的合理有效性。

2 新的证据组合方法

2.1 证据间的DICE相似度

信息检索技术中，DICE系数用来计算语句之间的相似度[12－13]。设语句向量是由L个索引关键词构成，S1＝ （w11，w12，…，w1L）和 S2＝ （w21，w22，…，w2L）分别表示两个语句向量。其中w1i表示第i个关键词在语句1中的权重，则S1和S2的DICE相似度为：

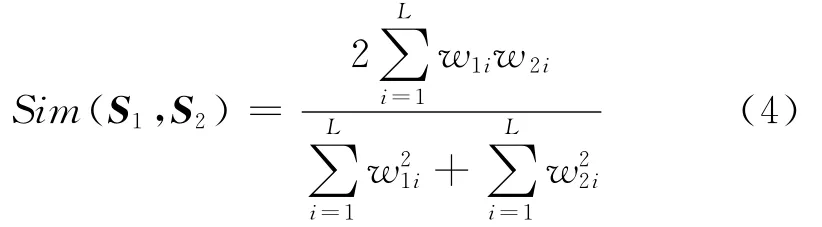
利用DICE系数来表征证据之间的相似度。设共有M 个证据体（m1，m2，…，mM）对辨识框架Θ＝ （A1，A2，…，AN）识别，其中mi＝ （mi1，mi2，…，miN），min表示证据体mi中命题n所获得的概率。则证据体mi和mk的相似度计算公式为：

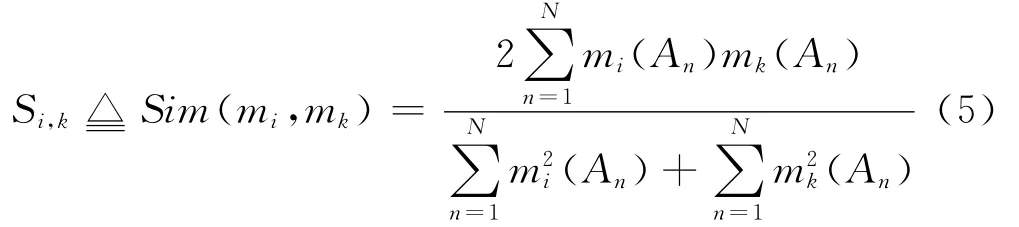
由定义可知，0≤Sim（mi，mk）≤1。

由此得到各证据之间的相似度矩阵为：

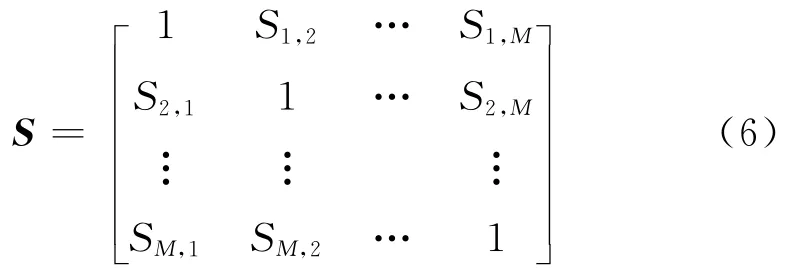
证据mi与其余（M－1）个证据的相似度之和为：

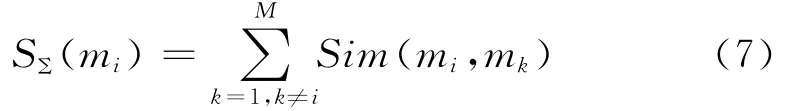
进一步得到mi与其它证据的平均相似度为：

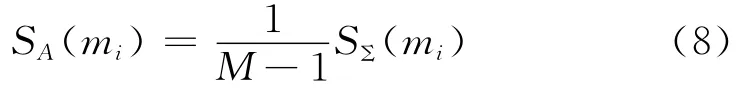
2.2 冲突性判定及修正

下面对各原始证据的冲突性进行判定，基本思想为：若某一证据与其它证据高度冲突，则该冲突证据与其它证据的平均相似度较小。判定方法如下：令S0表示所有证据之间的平均两两相似度，即：

以S0作为判决阈值，若SA（mi）＞S0，即证据mi与其它证据的平均相似度大于所有证据之间的平均相似度，则判定证据mi与其它证据的冲突性较小，无需进行修正。若SA（mi）≤S0，则判定证据mi与其它证据的冲突性较大，需要进行修正。修正方法为：用SA（mi）作为mi中原有焦元的修正系数，将不确定性概率1－SA（mi）按照如下的比例分配给各个焦元：

对于修正后的证据m′i，仍满足：

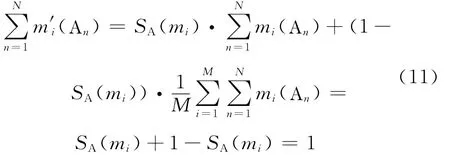
对于两个证据的组合，有SA（m1）＝SA（m2）＝S0，此时两个证据均由式（10）进行修正。

最后利用DS组合规则对修正后的各个证据进行组合，得到合成证据。

3 算例仿真

3.1 算例1

下面以文献[11]中的2证据组合为例来说明本算法的计算流程，辨识框架Θ＝｛Α，Β，C｝，2个证据体分别为m1＝ ｛0.9，0，0.1｝；m2＝ ｛0，0.9，0.1｝。

下面用本算法进行证据组合，由式（8）、式（9）求得两个证据相似度为：SA（m1）＝SA（m2）＝S0＝0.0122。两证据的算术平均证据为：＝｛0.495，0.01，0.495｝。由式（10）进行修正后的两个证据分别为：

运用DS组合规则对m′1和m′2进行组合，得到：

m1，2＝ ｛0.4880，0.4880，0.0241｝

表1给出了DS规则、Yager规则和本方法的组合结果。

表1 算例1的合成结果

对于算例1，冲突因子K＝0.99，此时两个证据高度冲突。命题C在两个原始证据中的概率都接近于0，但DS规则的组合结果中C成为确定性事件，而Yager规则将全部冲突概率赋予未知命题，两种规则的组合结果均否定了命题A和B，组合结果有悖常理。由于两个证据均以接近1的概率各支持命题A和B。则合成证据中A和B获得的概率应该基本相当。因此，本方法的组合结果是直观合意的。

3.2 算例2

采用文献[4]中的3证据组合算例，将本方法与DS方法、Yager方法、文献[4]方法以及文献[7－8]方法进行比较。辨识框架Θ ＝ ｛Α，Β，C｝，3个证据体分别为：m1＝ ｛0.98，0.01，0.01｝；m2＝ ｛0，0.01，0.99｝；m3＝ ｛0.9，0，0.1｝。下面给出本算法的计算流程：对于到来的前两个证据，计算过程与算例1类似，此处不再赘述，得到组合结果为：

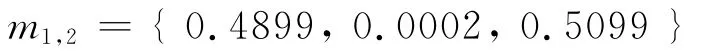
当第三个证据到来后，由式（8）可得：

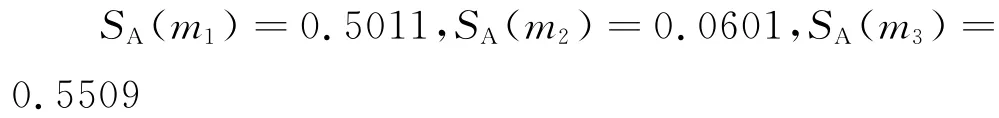
由冲突性判定方法可知证据m2为冲突证据，对其进行修正后，得到：

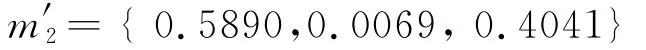
最后运用DS规则进行组合，得到合成证据为：

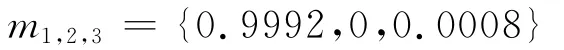
几种不同方法的组合结果如表2所示。

表2 算例2的合成结果

对表2中各种规则的组合结果进行分析可知，DS规则和Yager规则均不适合处理冲突证据的组合问题。DS规则对前两个高冲突证据的组合结果有悖常理，对3个证据的组合结果出现一票否决现象。Yager规则将冲突概全部赋给不确定性命题，且没有解决一票否决问题。文献[4]算法较DS规则和Yager规则更为合理，但从组合结果可以看出，无法从合成证据中获得对主命题的确定性决策，组合结果仍然相对保守。

以文献[7－8]为代表的证据平均组合法和文中的方法均能给出命题A的确定性决策。文献[8]在文献[7]方法的基础上，将证据间的关联考虑在内，因此具有比文献[7]方法更快的收敛速度。但是该类方法抛弃原始证据，以平均证据作为证据源，其合理性受到质疑[9－10]。

文中的方法通过对原始证据进行冲突性判定及修正，具有较好的组合结果。从表2可知，前两个证据均以接近1的概率各支持命题A和C，因此组合结果中A和C获得的概率基本相当。当第三个证据到来时，已经具有较为明显的倾向性。此时DS规则和Yager规则失效，文献[3]方法的组合结果过于保守，文献[7－8]方法的组合结果中命题A获得的概率分别为0.7449和0.8819。而文中方法的组合结果中命题A获得的概率为0.9992。因此，同以上几种方法相比，文中方法对三个证据的组合结果具有较快的收敛速度。

4 结论

针对DS规则在组合高度冲突证据时的失效问题，文中提出一种修改模型的冲突证据组合新方法。通过引入DICE相似度计算不同证据的可信度，获得可信度加权平均证据。并对各原始证据进行冲突性判定及修正。最后利用DS规则完成证据组合。修正过程中即利用了冲突证据的原始信息，又有效减少了冲突证据对最终组合结果的干扰。算例仿真表明文中算法能够有效处理冲突证据的组合问题，组合结果较为合理。

[1]Lefevre E，Colot O，Vannoorenberghe P.Belief function combination and conflict management[J].Information Fusion，2002，3（3）：149－162.

[2]Smets P.The combination of evidence in the transferable belief method[J].IEEE Trans.on Pattern Analysis and Machine Intelligence，1990，12（5）：447－458.

[3]Yager R R.On the Dempster－Schafer framework and new combination rules[J].Information Science，1989，41（2）：93－137.

[4]孙全，叶秀清，顾伟康.一种新的基于证据理论的合成公式[J].电子学报，2000，28（8）：117－119.

[5]李伟彤.一种冲突情况下的自适应证据理论合成公式[J].弹箭与制导学报，2006，26（3）：250－252.

[6]Haenni R.Comments on about the belief functions combination and the conflict management problem[J].Information Fusion，2002，3（4）：237－239.

[7]Murphy C K.Combining belief functions when evidence conflicts[J].Decision Support System，2000，29（1）：1－9.

[8]邓勇，施文康，朱振福.一种有效处理冲突证据的组合方法[J].红外与毫米波学报，2004，23（1）：27－32.

[9]林志贵，徐立中，周金陵.基于修改模型的冲突证据组合方法[J].上海交通大学学报，2006（1）：157－163.

[10]周皓，李少洪.GDOP引出的冲突证据组合新算法[J].控制与决策，2010，25（2）：278－281.

[11]林作铨，牟克典，韩庆.基于未知扰动的冲突证据合成方法[J].软件学报，2004，21（8）：46－52.

[12]陶跃华.基于向量的相似度计算方案[J].云南师范大学学报（自然科学版），2001，21（5）：20－23.

[13]Leo Egghe，Ronald Rousseau.Classical retrieval and overlap measures satisfy the requirements for rankings based on a Lorenz curve[J].Information Processing and Management，2006，42（1）：106－120.