植物有效成分间歇浸取动力学研究进展
2011-12-06曹雁平朱雨辰
曹雁平, 朱雨辰
(北京工商大学食品学院/食品添加剂与配料北京市高等学校工程研究中心,北京 100048)
植物有效成分间歇浸取动力学研究进展
曹雁平, 朱雨辰
(北京工商大学食品学院/食品添加剂与配料北京市高等学校工程研究中心,北京 100048)
介绍了植物有效成分间歇浸取动力学模型的理论基础、数学处理方法、发展沿革和研究进展.根据间歇浸取动力学模型特点将浸取动力学模型分为平衡浓度模型和瞬时浓度模型,详细介绍了两种模型的建立.大多数有关植物有效成分浸取动力学研究都是以平衡浓度模型为基础的,由于浸取过程中有效成分会参与反应或发生降解,真实的有效成分浸取平衡浓度很难测定,显然该模型对于易反应有效成分或微波、超声等强化浸取过程有不可克服的缺陷.瞬时浓度模型将广泛应用,但是数学处理难度增大.详细介绍了超声、微波等特殊物理场强化条件下浸取动力学方程建立的理论基础、数学方法和研究进展.
有效成分;植物;间歇浸取;动力学;模型
植物资源是人类赖以生存的主要资源,是一切可再生资源的基础.植物资源的开发利用事关化工、生物、食品、医药、日化等工业的生产和发展.其中关键技术之一就是浸取技术,是植物功能成分开发与利用的重要环节.浸取技术和工艺不仅直接影响植物功能成分的得率、纯度和生产成本,而且对资源可持续利用以及环境保护都有重要意义.浸取技术一直是研究的热点,但是浸取技术的发展离不开深入的相关技术基础研究,其中植物成分浸取过程动力学研究始终受到高度重视.
通常采用的浸取动力学研究方法有3种,1)完全从机理出发建立数学模型,常常因为对机理掌握的不完善,使得不能建立机理式数学模型或建立的机理式数学模型与实验结果差异很大,该方法是理想的方法;2)以一般的机理(Fick定律和质量守恒定律)为基础,结合实验数据,建立的半经验浸取动力学方程能较好地符合实验结果,但是普适性较差,常常只能在实验的条件范围内适用,该方法是目前应用最普遍的方法;3)根据实验数据拟合的描述性数学模型,不能利用该模型研究或讨论浸取过程,只能计算确定优化浸取条件.方法1)、2)都从物理模型入手,发展到数学模型.
浸取是化工单元操作之一,根据进出料的不同分为间歇浸取(batch extraction)、半连续浸取(semicontinuous extraction)和连续浸取(continuous extraction).间歇浸取由于设备简单、操作方便灵活而在工业生产中广为应用,绝大多数的浸取工艺研究和技术开发都是以间歇浸取为基础的,因此,有关浸取动力学研究也以间歇浸取动力学为主.浸取动力学研究发展复杂而漫长,人们进行了大量的尝试.
1 常规间歇浸取动力学研究
目前,有关间歇浸取动力学研究主要有平衡浓度类模型(稳态模型)和瞬时浓度类模型这两类.
Long[1]根据红茶中可溶成分的浸取速率数据,认为浸取速率符合一级溶解速率定律,涉及了平衡浓度的概念.Spiro等[2]将茶叶和咖啡豆假设为平板和球形,根据Fick第一定律有:

假设某时刻有效成分浓度梯度随时间递减速率与浓度梯度呈正比,即有:利用边界条件积分,将结果带入式(1)得到平衡浓度类模型:
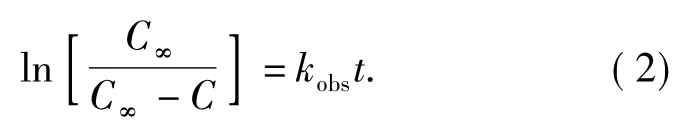
式(2)中:C为植物有效成分的浓度;C∞为浸取达到平衡时(C不再随时间t变化)植物有效成分的浓度;kobs为表观浸取速率常数;t为浸取时间.
针对茶叶有效成分的浸取,Spiro推导出了kobs的表达式:

式(3)右侧各项的大小确定了浸取过程的特征.
1) 如果 1/k-1最大,则 k'≈k-1,说明浸取过程是表面控制,这意谓溶液中的有效成分重新被吸附到叶子中;
2) 如果 Kd/2Dleaf最大,则 k'≈2Dleaf/Kd,说明浸取过程是有效成分在膨润的叶子内扩散速率控制阶段;
3) 如果 δ/Dsolu最大,则 k'≈Dsolu/δ,说明浸取过程是有效成分在液膜内扩散速率控制阶段.
如果扩散速率与搅拌速度无关,则可以确定浸取过程处于1)、2)阶段.
针对咖啡豆中咖啡因的浸取,Spiro推导出了kobs的表达式[3]:
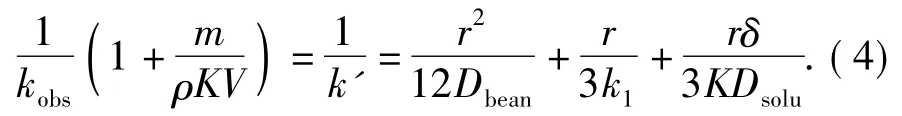
同样:
1)如果咖啡因在咖啡豆内的扩散是限制性步骤,k'=12Dbean/r2;
2)如果咖啡因穿过固液界面是最慢的步骤,k'=3k1/r;
3)如果咖啡因在Nernst layer边界层是限制性步骤,k'=3KDsolu/rδ.
式(4)反映了咖啡粒度对咖啡因浸取速率常数的影响.以上所讨论的都是极限情况,实际的浸取过程应该是混合情况.
该模型是Spiro以Fick第一定律为基础,即认为浸取是稳定过程,推导获得的,也被称为Spiro稳定态模型.
由于多数实验结果发现式(2)存在一个截距,可以认为是由于部分可溶性成分在浸取开始时快速溶入溶剂中,Price[4]将式(2)修正为:
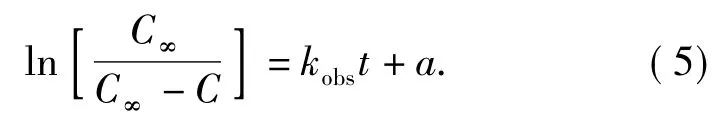
由于浸取工艺的不同,浸取过程存在差异,可以采用建立相应的物理模型,对平衡浓度类模型进行修正.
植物组织不同、预处理方法不同都会导致原料的结构差异很大,对浸取的影响也不同.根据在压榨加工使部分菜籽细胞发生破裂,大部分油脂被压榨而流到菜籽外,其余的一部分留在破碎细胞内和细胞间隙中,菜籽表面会附着一层油脂等现象,So[5]等提出压榨油菜籽中油脂浸取过程分为洗涤和扩散2个阶段,而且扩散阶段同时发生快速扩散和慢速扩散2个过程;在浸取开始的瞬间菜籽表面的油脂即被洗涤、溶入溶剂(洗涤过程);在破碎细胞和细胞间隙中的油脂因扩散阻力小会以较快的速度扩散到溶剂中(快速扩散过程);完好细胞中的油脂因扩散阻力大则会以较慢的速度扩散到溶剂中(慢速扩散过程);据此建立三项式模型为:
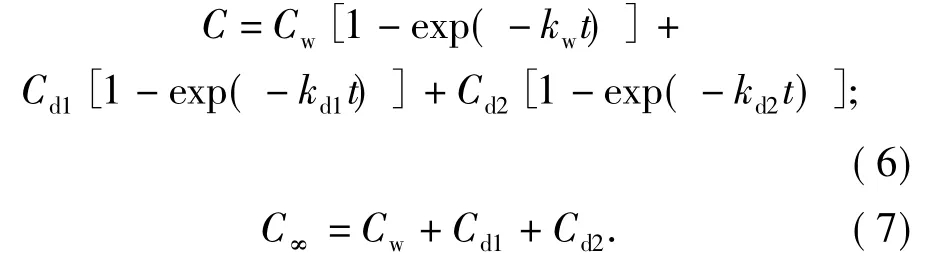
式(6)、(7)中,Cw为洗涤作用贡献的质量浓度;Cd1为快速扩散过程贡献的质量浓度;kd2为快速扩散过程速率常数;Cd2为慢速扩散过程贡献的质量浓度,kd2为慢速扩散过程速率常数,C∞为平衡时浸取液中菜籽油的质量浓度.
Spiro[6]根据实验数据将姜中姜辣素浸取分为快速的初始浸取、快速阶段和慢速阶段,也可以用So模型描述浸取动力学过程,因为含有姜辣素的油腺比其他植物组织更易受切片、粉碎等的破坏,部分姜辣素分布于颗粒表面,即 kw将很大,意谓着exp(-kwt)项趋于0,则浸取动力学模型为:
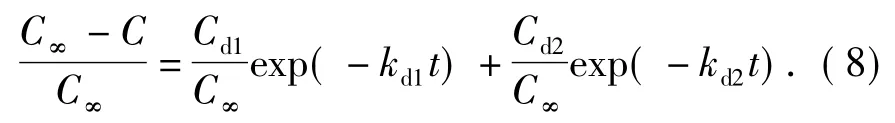
在浸取的前期,有效成分浓度C主要受快速浸取过程影响,因此,Cd1的作用远远大于Cd2,可以将Cd2视为常数且k2趋于0,则式(7)改写为:
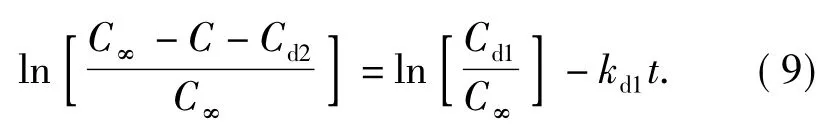
在浸取的后期,细胞破碎处的有效成分已在快速浸取阶段被浸出,则Cd1项可以忽略,有效成分浓度C主要受慢速浸取过程影响,因此则式(7)改写为:
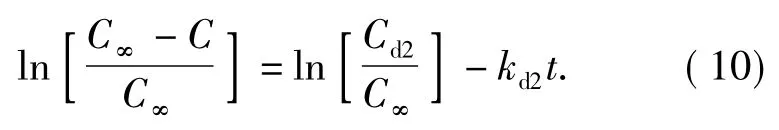
宋洪波等[7]根据红茶叶片组织结构分为细胞内、外空间的特点,将红茶颗粒内部分为细胞内的浸取高阻力区及细胞外和颗粒边缘破碎细胞的浸取低阻力区;低阻力区的组分直接向颗粒表面扩散,高阻力区的组分需经过低阻力区再向颗粒表面扩散.基于这一物理模型,建立两个浸取质量衡算微分方程,推导出与式(6)一致的浸取动力学方程.
Zanoni等[8]在研究不同粒度对热水浸取咖啡可溶成分的影响时,发现溶剂的洗涤效果与颗粒外表面积呈线性关系,而且浸取物的组成与浸取时间无关.而且咖啡中大多数可溶组分以极快的速率溶出,据此将咖啡浸取过程分为洗涤和扩散2个阶段,其中扩散阶段只是一个单一过程,相应的一级浸取过程动力学模型为:
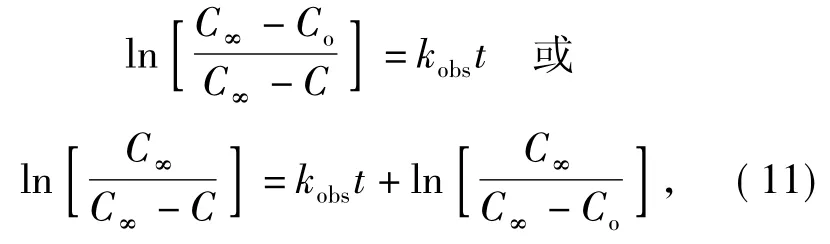
式(11)中:Co为初始有效成分浓度.
基于与Spiro同样理论模型,储茂泉[9]考虑提取时若中药颗粒在浸提前预先用适量溶剂浸润,则t=0时刻已有部分溶质溶入溶剂中,即t=0时C=Co,得到形式上与式(5)相同的模型.基于稳定过程的Fick第一定律和不稳定过程的Fick第二定律推导了中药有效成分浸提动力学方程,证明浸提动力学方程在形式上完全一致.因为,应用Spiro稳定态模型涉及植物有效浓度的浸取平衡浓度,所以可以称该模型为平衡浓度类模型.目前,大多数有关植物有效成分浸取动力学研究都是以该模型为基础的.
平衡浓度类模型应用时必须测出植物有效成分的浸取平衡浓度.而对于在浸取过程中会发生有效成分降解和参与反应的情况,因为C测=C浸-C降或C测=C浸-C反,以及怎么确定平衡浓度(应该是浸取时间无穷大时的浓度)等问题,使建立的平衡浓度类动力学方程很难真实反映浸取过程各因素对有效成分浸取的影响.显然,该类模型在微波、超声等物理场强化浸取过程方面会受到限制,因为微波、超声都是提供高能量的方法,许多微波浸取和超声浸取工艺或技术的研究结果显示,微波能量、超声能量与有效成分浓度和浸取率不是单调增长关系,而是有一极大值,说明植物有效成分在浸取过程中发生了变化[10].并且已有专门的研究证明植物有效成分在微波场[11]和超声场中发生了变化[12-13].即使在常规热浸取中,超过50℃也会造成某些成分发生变化[14].这是平衡浓度类模型的不足.
瞬时浓度类模型是储茂泉[15]以 Fick定律基础,根据林亚平[16]借鉴电解质溶液受电场、分子间作用下的扩散研究成果[17],认为扩散过程浓度梯度随时间变化规律符合幂函数关系dC/dx=atb,以及借鉴电解质溶液扩散研究成果[18],即扩散系数是溶质浓度的幂函数D=DoCn,得到植物有效成分浸取微分动力学方程:

积分得到:
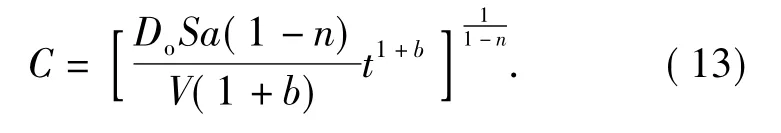
式(12)、(13)中,Do为仅与扩散体系的物质特性、温度等有关的常数,为与原扩散系数D区别,称为固有扩散系数;S为固液界面面积;a为参数,a>0;b为浓度减少指数,与浸取方式、传质过程特点、传质过程强化方式和程度、溶液性质等因素有关的系数,-1<b<0.n为参数,因浓度导致扩散系数变化的浓度衰减系数,与浓度减少指数相同,受温度、电场、超声场、黏度、分子间作用力大小等因素的影响,n<1;V为浸取液体积.
由于该模型仅关联瞬时浓度与各因素的关系,可以称为瞬时浓度模型,由于该模型多出两个参数,数学处理的难度加大.
储茂泉认为在药材的粒度过细时,浸取过程不再是内扩散控制过程,该模型不适合;而在溶剂倍量过小的情况时因溶剂量少会影响溶质的溶解,也会使模型偏离扩散控制过程,该模型也不适合.另外,对于绝大多数浸取过程,浸取液有效成分属于低浓度,则n=0或n≈0,而且超声等物理场能够强化传质过程,使局部高浓度的情况很少出现.
杨宏志等[19]利用此方法建立了溶剂法提取亚麻籽木脂素动力学模型,实验验证表明该模型具有误差小于7%的预测精度.
由于植物颗粒内部的有效成分浓度无法测量,有研究者将植物有效成分的浸取过程视为解吸过程,可以利用Langrniur等温方程与Freundlich等温方程等吸附动力学模型建立植物颗粒内和溶液有效成分之间联系的方法研究浸取过程动力学问题.
与前面介绍的浸取液浓度与时间的关系动力学模型不同,不稳定扩散模型(14)和Ponomaryov经验方程(15)建立了植物颗粒内部有效成分浓度与浸取时间的关系:
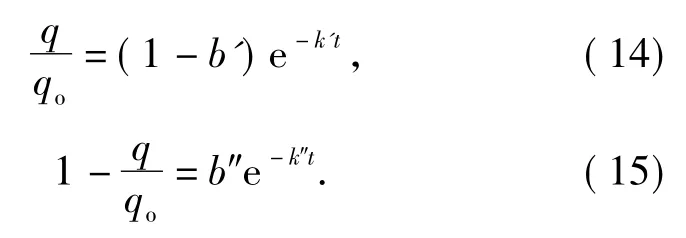
式(14)、(15)中,qo为植物颗粒内有效成分浓度;q为植物有效成分含量;b'、b″为常数;k'、k″为慢浸取过程的速率常数.
这两个模型在超声浸取过程的动力学研究中也有成功应用[20-21].
可见,平衡浓度模型、不稳定扩散模型和Ponomaryov经验方程都可以视为有效成分浓度(或得率)与时间的关系符合一级反应方程规律,则有:
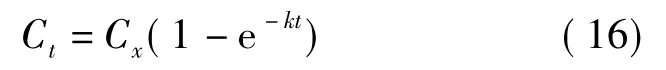
式(16)中,x为∞或0.
2 超声间歇浸取动力学研究
决定有效成分浸取难易程度有三方面的原因:1)不同的有效成分处于植物组织的不同部位,因为不同植物组织的结构和组成不同,对有效成分浸取的限制、阻碍不同;2)不同的有效成分与植物组织中其他不同成分的结合方式不同;3)不同溶剂在植物组织内部浸润、渗透的能力和对有效成分的溶解能力不同.因此,不同有效成分浸取需要克服的势垒不同,表现为浸取活化能差异很大,需要获得能量克服势垒.提供能量的形式有物理能和化学能.在植物有效成分的浸取中,主要是物理能,提供的方式有热能、电能和辐射能(光、声、射线等).
Khan等[22]直接利用实验数据求出浸取一级速率方程的速率常数.
黄可龙等[23]利用常规间歇浸取动力学的研究成果,结合了秦炜等[24]直接超声场的影响可采用超声场的热效应、管内流体扰动及相互作用参数叠加的方式表示的研究成果,即超声强化的浸取过程的扩散系数可以表示为:

式(17)、(18)中,DM为分子扩散系数;DE为涡流扩散系数,k1、k2、k3为温度 T、功率 P 及二者交互作用对扩散系数影响系数;D为浸取扩散系数.
将浸取扩散系数方程式代入依据Fick定律推导出来的动力学方程中,就得到超声强化的间歇浸取动力学方程.
Xu Huaneng等[25]在研究变幅杆式超声浸取系统的浸取动力学时,首先借鉴了Kanthale等[26]的研究成果,即以空化气泡群作为整体来研究超声空化效应,空化效应不仅与空化气泡群产生的压力有关,而且与空化气泡群的活化体积有关,超声强度I的影响为,空化压力Pc∝I0.330和活化体积VA∝I0.264;空化压力越高,活化体积越大,细胞破碎程度越高,导致细胞最小势垒μ越低,可假设细胞势垒最小值的变化与空化压力和活化体积的乘积成正比:

式(19)中,K1、K'1为比例系数;S为超声探头的横截面积;φ为超声声电效率;P为超声功率.对于特定的超声探头系统,在同一工作频率和一定的电功率输入范围内,声电效率可近似看作常数.徐化能等又借鉴了Guo等[27]系统研究超声强化结晶过程的结果,即组分的扩散系数随着超声的声压幅值增大而增大,其变化值和能量输入呈指数关系,即D'-D=k'1exp(k'2P);考虑到指数关系含有两个关联参数k'1、k'2,应用到模型方程时,将含有太多的拟合参数,不利于工程应用,提出假设(D'-D)也与空化压力和活化体积的乘积成正比,表示如下:
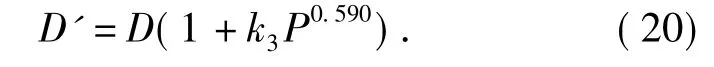
式(20)中,D'为变幅杆超声间歇浸取有效成分的扩散系数;D为常规间歇浸取有效成分的扩散系数;k3=(K'2/D)(φ/S)0.594,对于特定的溶剂可视为常数;K'2为比例系数.将式(20)引入常规间歇浸取动力学方程,建立变幅杆超声间歇浸取动力学方程,动力学计算值与实验值的平均误差为1.02%~2.40%,最大误差为2.10% ~5.17%,显然,建立的动力学方程等较好地反映了实验结果.
曹雁平等[28]借鉴秦炜等[24]确定超声功率对毛细管扩散的影响符合关系式:Du=(1+kTT+kPP)Dc;同时借鉴了Bercu[29]发现超声功率与超声空化作用(与扩散系数呈正比)符合幂函数关系式的研究成果,建立超声功率P、频率f等特性参数与扩散系数Du关系式为:
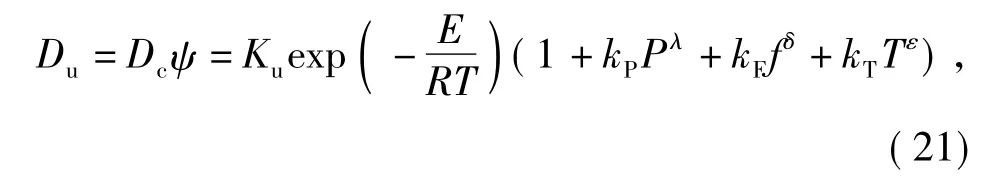
并建立包含超声功率、超声频率的瞬时浓度动力学模型,能够较好拟合实验数据.
Langrniur等温方程与Freundlich等温方程可以建立在溶液和原料中有效成分浓度的关系,适用于非超声和超声浸取过程.Ji Jianbing等[30]利用Langrniur等温方程,确立栀子内与溶液中栀子苷的平衡浓度关系:

式(22)中,q为平衡时栀子颗粒中栀子苷的浓度;K为常数;Q为栀子颗粒中栀子苷的含量;Cξ=1:在ξ=1时溶液中栀子苷的平衡浓度;ξ=r/R;r为栀子颗粒半径;R为固液边界层厚度.
液相传质方程为:

式(23)中,kf为传质系数;m为栀子的质量;ρ为栀子颗粒的真实密度;V为溶液的体积.
固相传质方程为:
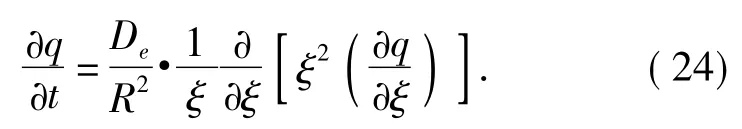
式中De为扩散系数.
式(23)和(24)是超声功率影响的栀子甙相平衡-传质动力学方程组,但是该相平衡-传质方程组没有解析解,需采用有限元差分法将方程离散,借助数学软件,通过参数拟合法求解理论溶液浓度与时间的关系、粒内有效扩散系数De和液膜传质系数kf.在该模型中没有直接反映超声功率等因素.
全学军等[31]认为受超声波直接作用的主要是粒子表面的植物细胞,细胞破碎有利于快速提取目标产物,而颗粒内部目标产物须经过扩散到达颗粒表面后,扩散穿过颗粒表面液膜进入液相主体中.研究发现,被充分分散在溶剂中的多细胞组成的植物颗粒先溶涨,颗粒表面处被破坏细胞的有效成分被浸出,因颗粒中细胞结构仍然比较完整,而呈现明显的空壳,形成一个核-壳结构.当颗粒在超声波作用下,核-壳结构中的核不断缩小,壳厚度增加,且其中的细胞结构被破坏变形.因此假设:1)核-壳界面细胞被超声波破坏击穿后形成的壳体是一种多孔介质,对有效成分的向外扩散不存在阻力;2)核在超声波作用下沿半径方向以同等的速度缩小,整个提取过程中颗粒几乎保持原形;3)超声波穿过多孔的壳体主要与核界面相互作用,通过击穿核界面层细胞而逐渐提取有效成分;4)在超声波与核界面层细胞作用时,核内部的细胞受超声波作用比界面上的作用小得多,并不被超声波击穿,不提取出有效成分,即在整个提取过程中,核的密度和有效成分含量几乎不变.由于随着超声波作用时间的延长,含有有效成分的核半径逐渐缩小,由此该模型称为无扩散阻力的有效成分核收缩模型(简称缩核模型).
假如整个提取过程总的提取速率主要由核界面层细胞的破坏速率决定,即提取控制步骤是核-壳界面上细胞的破碎过程,而细胞破坏速率又取决于超声波可以直接作用的核界面面积,并与此成正比.基于此,有效成分受细胞破碎控制情况下的动力学方程式:

式(25)中,η为有效成分提取百分率;δ'为超声波开始输入时有效成分核收缩率;k1为细胞破碎控制时的动力学速率常数.
另一方面,假如浸取的控制步骤不是核-壳界面细胞的破碎,而是有效成分由界面穿过壳层的扩散,并假定核-壳界面上有效成分浓度C1在浸取过程中几乎不变.在稳态条件下,忽略壳层中溶剂主体的流动,按照Fick第一定律,得到整个浸取过程有效成分受核外壳层扩散控制情况下的动力学方程:
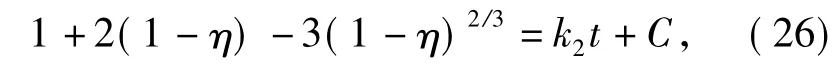
式(26)中,k2为核外壳层扩散控制时的动力学速率常数;Ma为有效成分分子量;Da为有效成分在壳层的扩散系数;C1为核-壳界面上有效成分浓度;ρ为植物颗粒密度;ro为颗粒在t=0时的半径;xo为植物颗粒中有效成分的百分含量.
建立的超声间歇浸取大豆异黄酮动力学方程的计算值与实验值的相关系数为R2=0.71~0.98,相关系数小于0.8的情况是因为机械搅拌的转速超过1 500 r·min-1后影响了超声场的作用.
3 发展与展望
为了研究浸取机理和便于应用,人们希望浸取动力学模型越简单越好,而往往简单模型的计算值与实验数据相差较大,即动力学模型不能很好地反映浸取过程.描述性模型的计算值与实验数据的拟合很好,但是也不能说描述性模型能很好地反映浸取过程,因为该模型不能反映各因素对浸取过程的影响,不能用于探讨浸取机理.
平衡浓度模型的影响无疑是巨大的,但是随着人们愈加重视浸取过程中目标成分的变化,瞬时浓度模型能更真实地反映浸取过程,更有利于对浸取机理的认识,在未来的浸取动力学研究中将发挥关键作用,不仅为预测及工艺条件优化提供准确的理论计算数据,同时也为浸取机理的理解、指导工艺改进和新工艺开发提供一定的理论基础.
[1]Long V D.Aqueous extraction of black leaf tea.Ⅲ.Experiments with a stirred column[J].International Journal of Food Science and Technology,1979,14(5):449-462.
[2]Spiro M,Jago D S.Kinetics and equilibria of tea infusion Part 3-Rotating-disc experiments interpreted by a steadystate model[J].Journal of the Chemical Society Faraday Transactions,1982,78,295-305.
[3]Spiro M,Selwood R M.The kinetics and mechanism of caffeine infusion from coffee:The effect of particle size[J].Journal of the Science of Food and Agriculture,1984,35(8):915-924.
[4]Price W E.Kinetics and equilibria of tea infusion[D].London:University of London,1985.
[5]So G C,Macdonald D G.Kinetics of oil extraction from canola(rapeseed)[J].The Canadian Journal of Chemical Engineering,1986,64(1):80-86.
[6]Spiro M,Kandiah M.Extraction of ginger rhizome:kinetic studies with acetone[J].International Journal of Food Science and Technology,1989,24(6):589-600.
[7]宋洪波,毛志怀,Lian C.植物物料红茶的浸提动力学研究[J].农业工程学报,2005,21(3):24-28.
[8]Zanoni B,Pagliarini E,Peri C.Modelling the aqueous extraction of soluble substances from ground rousted coffeed[J].Journal of the Science of Food and Agriculture,1992,58(2):275-279.
[9]储茂泉.中药提取过程的动力学及丹参酮剂型的研究[D].上海:华东理工大学,2001:15-16.
[10]曹雁平,刘佐才.植物有效成分超声浸取研究现状[J].化工进展,2005,24(11):1249-1252.
[11]Wang R,Zhou W B,Wen R A H.Kinetic study of the thermal stability of tea catechins in aqueous systems using a microwave reactor[J].Journal of Agricultural and Food Chemistry,2006,54(16):5924-5932.
[12]曹雁平.茶叶有效成分的双频超声浸取研究[D].北京:北京理工大学,2006.
[13]Yang Bao,Jiang Yueming,Zhao Mourning,et al.Effects of ultrasonic extraction on the physical and chemical properties of polysaccharides from longan fruit pericarp[J].Polymer Degradation and Stability,2008,93(1):268-272.
[14]Pinelo M,Rubilar M,Sinciro J,et al.Extraction of antioxidant phenolics from almond hulls(Prunus amygdalu,s)and pine sawdust(Pinu,s pinaster) [J].Food Chemistry,2004,85(2):267-273.
[15]储茂泉.中药提取过程的动力学及丹参酮剂型的研究[D].上海:华东理工大学,2001:15-16.
[16]林亚平,卢维伦.非溶蚀型药物体系的释放动力学新模型——Fick第一扩散定律的修正及其应用[J].药学学报,1997,32(11):869-873.
[17]黄子卿.电解质溶液理论导轮[M].北京:科学出版社,1983:186-187.
[18]安特罗波夫.理论电化学[M].吴仲达,朱耀武,吴万伟,译.北京:高等教育出版社,1982:137-139.
[19]杨宏志,田伟,贾建.溶剂法提取亚麻籽木脂素动力学模型的建立[J].中国粮油学报,2007,22(2):75-78.
[20]Veliˇc'ckovi D T,Milenovi'c D M,Risti'c M S,et al.Kinetics of ultrasonic extraction of extractive substances from garden(Salvia officinalis L.)and glutinous(Salvia glutinosa L.)sage[J].Ultrasonic Sonochemistry,2006,13(2):150-156.
[21]Ivana T Stanisavljevi'c M L,Lazi'c V B Veljkovi'c.Ultrasonic extraction of oil from tobacco(Nicotiaha tabacurn L.)seeds [J].Ultrasonic Sonochemistry,2007,14(5):646-652.
[22]Khan M K,Abert-Vian M,Anne-Sylvie Fabiano-Tixier,et al.Ultrasound-assisted extraction of polyphenols(fla-vanone glycosides)from orange(Citrus sinensis L.)peel[J].Food Chemistry,2010 ,119(2):851-858.
[23]黄可龙,李进飞,刘素琴.超声场强化中药有效成分提取动力学模型[J].化工学报,2004,55(4):646-648.
[24]秦炜,张英,戴猷元.超声场对毛细管内电解质扩散系数的影响[J].清华大学学报:自然科学版,2001,41(6):41-43.
[25]Xu Huaneng,Zhang Yingxin,He Chaohong.Ultrasonically assisted extraction of isoflavones from stem of Pueraria lobata(Willd.)Ohwi and its mathematical model[J].Chinese Journal of Chemical Engineering,2007,15(6)861-867.
[26]Kanthale P M,Gogate P R,Pandit A B,et al.Cavity cluster approach for quantification of cavitational intensity in sonochemical reactors[J].Ultrasonics Sonochemistry,2003,10(4-5):181-189.
[27]Guo Z,Jones A G,Li N.The effect of ultrasound on the homogeneous nucleation of BaSO4during reactive crystallization[J]. ChemicalEngineering Science,2006,61(5):1617-1626.
[28]曹雁平,矫庆泽.超声功率、频率对姜黄素浸取的影响与动力学模型[J].高校化学工程学报,2011,25(2):212-218.
[29]Bercu V,Martinelli M,Massa C A,et al.A study of the deep structure of the energy landscape of glassy polystyrene:The exponential distribution of the energy barriers revealed by high-field electron spin resonance spectroscopy[J].Journal of Physics:Condens.Matter.,2004,16:L479-L488.
[30]Ji Jianbing ,Lu Xianghong,Cai Meiqiang,et al.Improvement of leaching process of Geniposide with ultrasound[J].Ultrasonic Sonochem,2006,13(5):455-462.
[31]全学军,王万能,陆天健.超声提取植物有效成分的动力学研究[J].化学反应工程与工艺,2005,21(4):320-326.
(责任编辑:叶红波)
Research Progress on Kinetic Models for Batch Extraction of Active Components from Plants
CAO Yan-ping,ZHU Yu-chen
(School of Food and Chemical Engineering/Beijing Higher Institution Engineering Research Center of Food Additives and Ingredients,Beijing Technology and Business University,Beijing 100048,China)
The research progress on kinetic models for batch extraction of active components from plants was reviewed in this paper,focusing on its theoretical basis and mathematical methods.According to the features of the batch extraction,the kinetic model of extraction was categorized as the equilibrium concentration model and the instantaneous concentration model.These two types of models were both introduced in details.Although the equilibrium concentration model was applied in most of the researches,it became problematic in the processes of microwave or ultrasonic extractions,especially when the active components were reactive or ready to decompose ,in which the equilibria were hardly reached.In these cases,the instantaneous concentration model could be widely used,which,however,increase the difficulties of mathematical treatment.The theoretical basis,mathematical methods and development of the kinetic equations of extractions assisted with special physical field such as ultrasound and microwave were also introduced in this paper.
active components;plants;batch extraction;kinetics;model
TS201
A
1671-1513(2011)06-0020-07
2011-07-01
国家“十二五”科技支撑计划资助项目(2011BAD23B02).
曹雁平,男,教授,博士,主要从事天然产物化学方面的研究.
