长白山天池火山千年大喷发空降浮岩碎屑的形貌特征和最终沉降速度

于红梅 许建东 林传勇

(中国地震局地质研究所，北京 100029)

长白山天池火山千年大喷发空降浮岩碎屑的形貌特征和最终沉降速度

于红梅 许建东 林传勇

(中国地震局地质研究所，北京 100029)

碎屑的形貌参数是计算碎屑最终沉降速度公式中的一个重要参数，而以往在计算中只是把碎屑假设为球形或椭球形，未对其进行详细研究。通过对长白山天池火山千年大喷发产生的空降碎屑的形貌分析得到一些新的认识:空降碎屑以浮岩为主，浮岩碎屑的形态不规则，从等轴状到拉长状，从次圆状到棱角状都有。随着浮岩碎屑粒径的减小，颗粒拉长现象明显，拉长碎屑的比例从15.02%上升到47.5%。并且，浮岩碎屑的粒度越小，颗粒棱角状越明显。通过对样品的形貌分析，得到其平均形态参数F=0.72。如果假设长白山天池火山千年大喷发浮岩碎屑为球形(F=1)时，计算的最终沉降速度是浮岩碎屑形态参数F=0.72时最终沉降速度的1.52倍，而当假设颗粒为椭球(F=0.5)时，计算的最终沉降速度是浮岩碎屑形态参数F=0.72时最终沉降速度的0.89倍。风速为10m/s时，不同形态参数的碎屑的沉积等厚线图显示，火山碎屑的扩散范围随着形态参数F值的减小而扩大。以上分析充分说明，碎屑的形貌特征对其最终沉降速度和扩散范围都具有较大的影响，今后在模拟火山碎屑扩散和灾害预测时应该充分加以考虑。

浮岩碎屑 形貌参数 最终沉降速度 扩散模型 长白山天池火山

0 引言

爆炸式火山喷发产生的碎屑的扩散和堆积与火山喷发柱(volcanic plume)的动力学密切相关，而火山喷发柱的动力学则强烈取决于风和喷发柱的相互作用:当喷发柱上升速率大于风速时形成强喷发柱，而当上升速率小于风速时形成弱喷发柱(Sparks et al.，1997;Bonadonna et al.，2003)。碎屑的沉降过程主要受风的平流和火山碎屑颗粒最终沉降速度的影响。Bonadonna等(1998)指出，碎屑颗粒的沉降状态明显影响火山碎屑堆积的减薄速率。因此，最终沉降速度的正确计算对火山碎屑堆积的模拟起着关键作用。Kunii等(1969)、Wilson等(1979)、Suzuki(1983)、Dellino等(2005)等均提出过计算火山碎屑颗粒最终沉降速度的公式。但是，目前火山碎屑扩散范围的模拟通常采用Suzuki(1983)的二维扩散模型(赵谊等，2002;赵谊，2003;于红梅等，2007)，而该模型应用的碎屑最终沉降速度是Suzuki(1983)通过对实际测量数据的统计得到的经验公式:

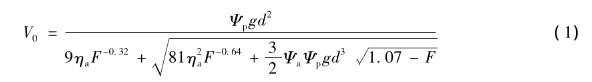
式(1)中，V0为碎屑颗粒最终沉降速度，d是近椭球状碎屑颗粒主轴平均直径，d=(a+b+c)/3，a、b和c分别为近椭球状碎屑的长轴、中间轴和短轴，ηa、Ψa分别为空气的黏度和密度，Ψp为碎屑颗粒的密度，g为重力加速度，F为碎屑颗粒的形态参数，F=(b+c)/2a。

由式(1)可见，碎屑颗粒的形态参数是计算碎屑颗粒最终沉降速度的一个重要参数。但是，在对火山碎屑的扩散进行模拟时，这些数据经常缺失，火山碎屑通常被假设为球形或椭球形(Heffter et al.，1993;Searcy etal.，1998;Bonadonna etal.，2005;Macedonio etal.，2005;Pfeiffer et al.，2005)。因此，开展火山碎屑颗粒的形貌特征分析以获得准确的形貌参数和最终沉降速率，对火山碎屑扩散和堆积的模拟具有十分重要的意义。于红梅等(2007)也曾对长白山天池火山千年大喷发的火山碎屑扩散范围进行过模拟，模拟时同样将碎屑颗粒假定为椭球形，采用的碎屑形态参数F为0.5，未对碎屑形貌特征进行详细的研究。为此，本文以长白山天池火山千年大喷发空降浮岩碎屑为例，探讨这些碎屑的形貌特征及其对最终沉降速度和扩散范围的影响。

1 采样概况

长白山天池火山坐落于吉林省东部中朝边境上，是一座具有潜在喷发危险性的中央式复合火山，其全新世喷发初步分为5000年前、4000年前、公元1199—1200年、公元1668年及1702年等(刘若新，2000)。其中，1199—1200年爆发时喷出的火山灰扩散到远至日本海及日本北部，造成的破坏相当严重，被认为是近2000年来全球最大规模的火山喷发之一(Machida et al.，1983;Machida et al.，1990;刘若新，2000)。由此，该次喷发也被称为长白山天池火山千年大喷发(魏海泉等，2004;史兰斌等，2005;樊祺诚等，2005;杨清福等，2007)。

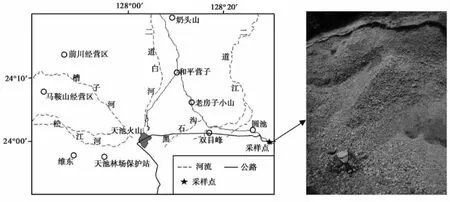
图1 长白山天池火山千年大喷发空降碎屑采样位置图Fig.1 Sampling site of the tephra fallout erupted during Millennium eruption of the Changbaishan Tianchi volcano.

由于受到喷发时风向的影响，天池火山喷发形成的空降碎屑堆积多集中分布于火山口以东及东南方向。考虑到本研究的主要目的是探讨千年大喷发空降碎屑的形貌特征及其最终沉降速度，取样位置选择在距离火口东约35km的圆池至钓鱼台的公路旁(图1)。此处公路两侧均覆盖了约1m厚的灰白色空降浮岩碎屑，碎屑呈正粒序，分选好，较干净，且出露面积较广。同时，根据刘若新等(2000)和尹金辉等(2005)的14C测年数据，该处确实属于千年大喷发的空降碎屑堆积物。

2 碎屑形貌的特征分析

根据对样品的宏观和镜下观测，长白山天池火山千年大喷发空降碎屑由浮岩、岩屑、晶屑及少量的玻屑等组成。其中，碱流质浮岩是最为主要的成分，尤其是2mm以上的碎屑几乎均为浮岩，而＜2mm的碎屑，浮岩也占20%～30%。因此，本次主要分析浮岩碎屑的形貌特征。首先利用振动筛把碎屑筛分为不同的粒级，并以φ=-log2(d)来表示，d为颗粒的直径，单位:mm。根据筛分结果，碎屑粒度在0.125～20mm之间(-4φ～3φ)。然后，以1φ为粒级间距对每一粒级的碎屑进行称重，得到每一粒级下的碎屑质量分数，并做出粒度分布直方图 (图2)。由图2可见，本样品碎屑粒径较大，1mm以上的碎屑颗粒占99%。根据粒度分析得到该碎屑样品的粒度标准偏差 σ =0.85，中间粒径 Mφ=-2.55。

在粒径＞0.25mm(2φ)的浮岩中选择1,178个碎屑进行形貌特征分析。由于＜0.25mm的浮岩碎屑不易挑选，而且处理时容易破碎，所以未对＜0.25mm粒径的碎屑进行研究。首先对碎屑颗粒进行图像拍摄，对于粒径＞4mm的颗粒可采用数码相机直接拍摄，而粒径＜4mm的颗粒则需用安装有数码相机的体视显微镜来拍摄。这样做是因为体视镜的视域有限，对于较大的颗粒不能完全拍摄，而对于细小的颗粒直接利用数码相机拍摄分辨率不足。拍摄时注意避免颗粒之间的接触和重叠，并标出比例尺。所获图像可利用Photoshop软件进行灰度、色阶、亮度等处理，使图像转化为清晰的二元图像，如图3所示。注意，处理时不要把颗粒边缘信息丢失或修改，尽量保持颗粒的原有形貌。另外，保存二元图像时要保存为NIH Image软件可识别的格式，例如tif、emf格式等。最后把二元图像导入可在网上免费下载的NIH Image软件中，利用该软件获得二元图像中颗粒的形态参数(Russ，1995;Dellino etal.，1996;Riley etal.，2003)。

图2 长白山天池火山千年大喷发空降碎屑粒度分布直方图Fig.2 Particle size distribution histogram of tephra particles erupted during Millennium eruption of Changbaishan Tianchi volcano.

利用NIH Image图像分析软件可以测定碎屑颗粒最小外切矩形的长度、宽度，颗粒最佳拟合椭圆的长轴和短轴，颗粒的面积和周长等。其中，面积为颗粒所包含的所有像素的总和，周长为围绕颗粒边界的长度。在此基础上，便可计算表征颗粒形貌的几个主要参数(Dellino et al.，1996;Coltelli et al.，2008):长宽比(aspect ratio)(AR)，定义为颗粒最佳拟合椭圆的短轴/最佳拟合椭圆的长轴，它反映颗粒的整体拉长程度，但不能区分方形和圆形;形状因子(form factor)(FF)，定义为4×π×面积/周长2，它表征颗粒的不规则程度或粗糙度(Russ，1995);压缩度(compactness)(CC)，定义为面积/(最小外切矩形的长度×最小外切矩形的宽度);矩形度(rectangularity)(RT)定义为周长/(2×最小外切矩形的长度+2×最小外切矩形的宽度)。

上述用来表征碎屑颗粒的形貌特征的参数，仅取决于碎屑颗粒宽度、长度、面积和周长之间的比值，因此它们是无量纲的参数，不取决于碎屑颗粒的大小。这些无量纲参数就避免了可能产生的测定误差，这也正是该方法的优点之所在。

图3 浮岩碎屑形貌图像Fig.3 Images of pumice pyroclasts.

3 形貌参数讨论

计算所有碎屑形貌参数(AR、FF、CC和RT)的平均值、标准差和中位数，结果列于表1中，并制作不同粒级下浮岩碎屑的AR、FF、CC和RT频率分布图(图4)。

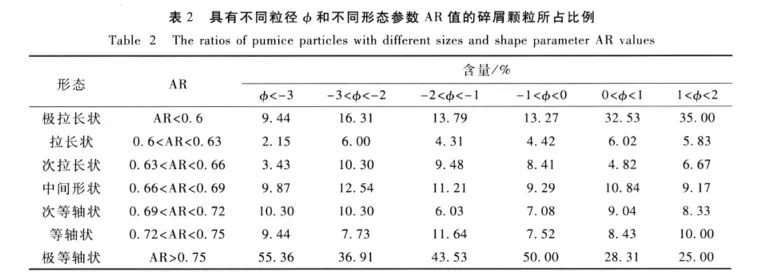
由图4和表1可见，AR值范围较宽，介于0.29～1之间。随着粒径的减小AR的平均值呈下降趋势，从0.760降为0.660，中位数从0.765降为0.663。可见浮岩碎屑的粒径越小，颗粒拉长现象越明显。根据Folk(1974)，火山碎屑颗粒可以分为极拉长状(AR＜0.6)、拉长状(0.6＜AR ＜0.63)、次拉长状(0.63 ＜ AR ＜0.66)、中间形状(0.66 ＜ AR ＜0.69)、次等轴状(0.69＜AR＜0.72)、等轴状(0.72＜AR ＜0.75)和极等轴状(AR ＞0.75)。我们统计每个粒级范围内的AR值，结果见表2。由表2可见，随着粒径的减小，极等轴状颗粒的比例呈减小趋势，极拉长状颗粒的比例呈增加趋势。对于粒径＞8mm(φ＜-3)的浮岩碎屑，极拉长状碎屑占9.44%，极等轴状碎屑占55.36%;而粒径在0.25～0.5mm(1＜ φ ＜2)之间的浮岩碎屑，极拉长状碎屑占35%，极等轴状的碎屑只占25%。

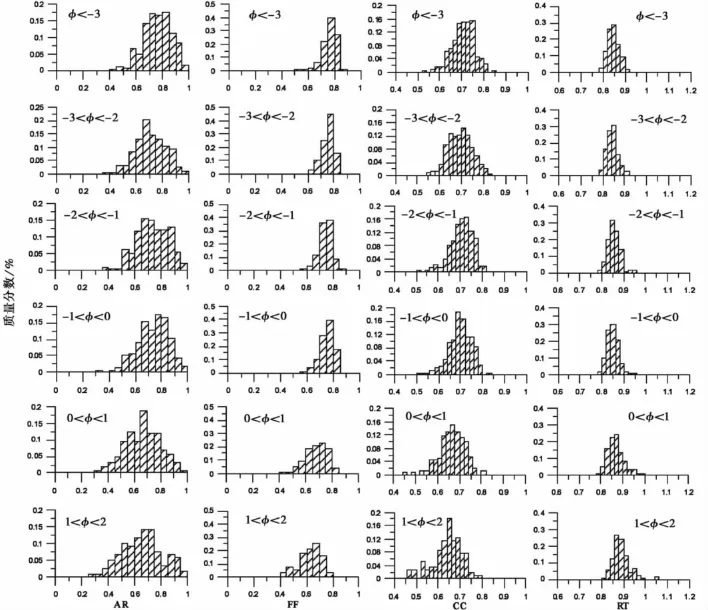
图4 不同浮岩碎屑粒径下AR、FF、CC和RT频率分布Fig.4 Frequency distribution of the AR，FF，CC and RT values calculated for different grain-size classes of the pumice pyroclasts.

CC值范围在0.44～0.84之间。CC值接近1，代表近矩形;接近0.785，代表近椭圆形，并且CC值越小，颗粒表面越不光滑(Dellino et al.，1996)。随着粒径的减小CC平均值呈下降趋势，从0.707降为0.664，中位数从0.709降为0.654。从图4也可以看出，随着粒度减小，直方图向左偏移，说明碎屑颗粒表面越来越不光滑。

FF值范围在0.42～0.86之间，随着粒径的减小，FF平均值减小。RT值范围在0.79～1.05之间，随着粒径的减小，RT平均值增大。利用FF和RT可以确定颗粒表面的不规则程度(Coltelli etal.，2008)。Muller(1967)根据碎屑形状把碎屑从极圆状到棱角状分为5个等级，并给出 Russel，Taylor，and Pettijohn对比图(图5)。利用NIH Image软件，求得图5中颗粒的形貌参数FF和RT值 (表3)，并制作FF和RT值与碎屑形状关系图(图6)。把本次统计的长白山天池火山空降碎屑的FF和RT值投点到图6中，可以确定浮岩碎屑的粒度越小，颗粒棱角状越明显。由图6可见，粒径＞1mm(φ＜0)的浮岩碎屑属于次圆状，0.5～1mm(0＜φ＜1)的碎屑属于次棱角状，0.25～0.5mm(1＜φ ＜2)的碎屑属于棱角状。

根据以上对浮岩碎屑形貌的分析可知，随着粒径的减小，拉长碎屑的比例呈增加趋势，从15.02%上升到47.5%。碎屑表面不规则，尤其是0.5～1mm(0＜φ ＜1)碎屑属于次棱角状，＜0.5mm(φ ＞1)的碎屑属于棱角状。显然，在计算这些拉长的、棱角状的浮岩碎屑的最终沉降速度时，需要充分考虑碎屑形貌的影响。

图 5 Russel，Taylor，and Pettijohn 对比图(引自 Muller，1967)Fig.5 Comparative chart of Russel，Taylor，and Pettijohn(after Muller，1967).

4 颗粒形态对最终沉降速度和扩散范围的影响

由于我们只是进行二维分析，根据以往文献(Wilson et al.，1979;Coltelli et al.，2008)，一般假设碎屑第3个轴等于二维确定的短轴，即b=c，所以颗粒的形态参数F=(b+c)/2a=b/a，即AR值。因此，由本文所分析的浮岩碎屑的平均AR值可以获得形态参数的平均值为F=0.72。然后，应用Suzuki经验公式(公式1)计算最终沉降速度。为了对比碎屑形态参数对其最终沉降速度的影响，同时还计算了颗粒为圆球(F=1)和椭球(F=0.5)时的最终沉降速度。计算时浮岩密度取为1.0g/cm3①陈文寄，樊祺诚，尹功明，等，2000，三个火山区的喷发历史、规模、物理及化学过程和构造地质背景研究，课题(95-11-03)研究报告。，得到的结果见图7。

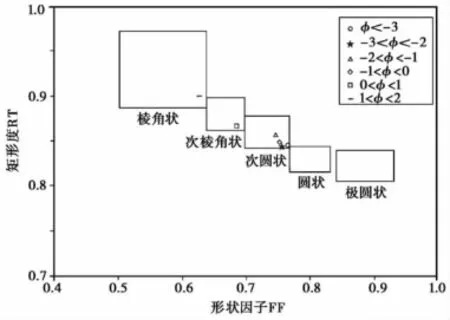
图6 碎屑形貌分析获得的FF与RT图Fig.6 FF vs RT plot of the values obtained by themorphological analysis.

由图7可见，碎屑的形貌对其最终沉降速度影响较大。例如，当颗粒直径为8mm时，浮岩碎屑形态参数F=0.72时最终沉降速度为8.2m/s，而假设碎屑为球形(F=1)的最终沉降速度为12.3m/s，假设碎屑为椭球(F=0.5)的最终沉降速度为7.3m/s;当颗粒直径为0.25mm时，3个速度值分别为0.97m/s、1.27m/s和0.86m/s。拟合3组最终沉降速度的数据，得到它们的关系如下

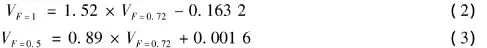
式中，VF=1是浮岩碎屑为球形(F=1)时的最终沉降速度，VF=0.72是浮岩碎屑形态参数为F=0.72时的最终沉降速度，VF=0.5是浮岩碎屑为椭球形(F=0.5)时的最终沉降速度。

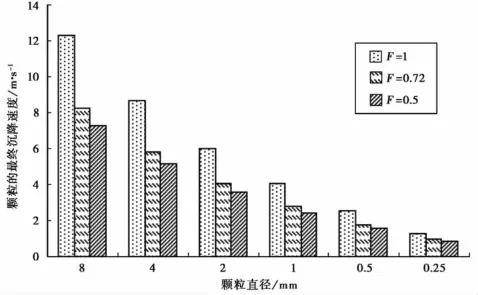
图7 不同形态参数(F)得到的最终沉降速度Fig.7 Terminal settling velocities for different shape parameters(F).

为了研究碎屑形貌对最终空降碎屑扩散范围的影响，我们对碎屑形态参数F=1、F=0.72和F=0.5分别进行了扩散模拟。模拟时将风速设为10m/s，其它参数参考刘若新等(1998)，见表4。根据模拟结果画出碎屑沉积厚度等值线图(图8)。由图8中可见，厚度分别在1000cm、100cm、20cm和10cm处，F=0.5时扩散的范围最广，F=0.72次之，F=1时扩散范围最小，说明形态参数F值越小扩散范围越远。由此也证明了碎屑的形貌特征对扩散范围具有较大的影响。

应当指出，上述模拟结果与长白山天池千年大喷发空降碎屑的实测等厚图有一定的差异，这可能和所采用的参数有关。但是，我们这里强调的是碎屑形貌特征对扩散范围的影响，尽管模拟结果有所偏差，仍可明显看出碎屑颗粒形貌对扩散范围的较大影响。

图8 不同碎屑形状参数时沉积厚度等值线对比图Fig.8 Isopach map of tephra for different shape parameters.点划线为F=0.5;实线为F=0.72;虚线为F=1;单位:cm

5 初步讨论

根据以上分析，本文获得了以下初步结论:

(1)长白山天池火山千年大喷发空降碎屑以浮岩为主，浮岩碎屑的形态很不规则，从等轴状到拉长状，从次圆状到棱角状都有。随着浮岩碎屑粒径的减小，颗粒拉长现象明显，拉长碎屑的比例从15.02%上升到47.5%。并且，浮岩碎屑的粒度越小，颗粒棱角状越明显，＞1mm的浮岩碎屑属于次圆状，0.5～1mm的碎屑属于次棱角状，0.25～0.5mm的碎屑属于棱角状。

(2)通过对样品的形貌分析，得到其平均形态参数F=0.72。如果假设长白山天池火山千年大喷发浮岩碎屑为球形(F=1)时，计算的最终沉降速度是浮岩碎屑形态参数F=0.72时最终沉降速度的1.52倍左右，而当假设颗粒为椭球(F=0.5)时，计算的最终沉降速度是浮岩碎屑形态参数F=0.72时最终沉降速度的0.89倍左右。

(3)风速为10m/s时，不同的碎屑形态参数的沉积厚度等值线图显示:形态参数F=0.5时，扩散的范围最广，F=0.72时次之，F=1时扩散范围最小，说明火山碎屑的扩散范围随着形态参数F值的减小而扩大。

以上的分析表明，碎屑的形貌特征对最终沉降速度和扩散范围都具有较大的影响。本次对＜0.25mm的碎屑未进行形貌分析，而体视镜下观察它们的形态更为不规则。因此，如果按球形计算这些碎屑的最终沉降速度，产生的误差必然会更大。显然，为了更为准确地模拟和预测火山喷发碎屑的扩散范围，需要对火山碎屑的形貌进行更为详尽的特征分析。此外，本次研究的主要目的是讨论碎屑形貌对最终沉降速度和扩散范围的影响。在研究过程中我们发现，不同粒径下碎屑颗粒的形貌参数有所不同，而以往在火山碎屑扩散模型中浮岩碎屑形态参数值取的是一个定值，未详细区分不同粒级下的形貌参数的变化，显然也是会造成较大的误差，更何况空降碎屑中还含有岩屑、晶屑、玻屑等其它成分，它们具有不同的形貌参数(Riley etal.，2003)。因此，在实际火山空降物灾害模拟时这些因素都应该加以考虑。还应指出的是，本研究中的最终沉降速度公式中只应用了AR参数，相信今后随着对颗粒最终沉降速度与其形貌参数之间关系的更深入了解，其它的参数(如CC、FF和RT等)也可以应用到公式中。

樊祺诚，隋建立，孙谦，等.2005.天池火山千年大喷发的岩浆混合作用与喷发机制初步探讨［J］.岩石学报，21(6):1703—1708.

FAN Qi-cheng，SUI Jian-li，SUN Qian，et al.2005.Preliminary research ofmagmamixing and explosivemechanism of themillennium eruption of Tianchi volcano［J］.Acta Petrologica Sinica，21(6):1703—1708(in Chinese).

刘若新，魏海泉，李继泰，等.1998.长白山天池火山近代喷发［M］.北京:科学出版社.83—107.

LIU Ruo-xin，WEIHai-quan，LI Ji-tai，et al.1998.The Recent Eruption of Tianchi Volcano，Changbaishan Mountains［M］.Science Press，Beijing.83—107(in Chinese).

刘若新.2000.中国的活火山［M］.北京:地震出版社.17—31.

LIU Ruo-xin.2000.The Active Volcanoes in China［M］.Seismological Press，Beijing.17—31(in Chinese).

史兰斌，陈孝德，杨清福，等.2005.长白山天池火山千年大喷发不同颜色浮岩的岩石化学特征［J］.地震地质，27(1):73—82.

SHILan-bin，CHEN Xiao-de，YANG Qing-fu，et al.2005.Petrochemistry of pumices of various colors produced by the eruption of Changbaishan Tianchi volcano at 1000 years ago［J］.Seismology and Geology，27(1):73—82(in Chinese).

魏海泉，金伯禄，刘永顺.2004.长白山天池火山地质学研究的若干进展与灾害分析［J］.岩石矿物学杂志，23(4):305—312.

WEIHai-quan，JIN Bo-lu，LIU Yong-shun.2004.Some advances in the study of volcanic geology and a hazards analysis of Tianchi volcano［J］.Acta Petrologica etMineralogica，23(4):305—312(in Chinese).

杨清福，史兰斌，张羽，等.2007.长白山天池火山千年大喷发火山碎屑流堆积的粒度特征与地质意义［J］.地震地质，29(3):480—491.

YANG Qing-fu，SHI Lan-bin，ZHANG Yu，et al.2007.Grain-size characteristics of themillennium pyroclastic flow depoits of Tianchivolcano and their geological implications［J］.Seismology and Geology，29(3):480—491(in Chinese).

尹金辉，郑勇刚，刘粤霞.2005.长白山天池火山炭化木的14C年代及其意义［J］.地震地质，27(1):83—88.

YIN Jin-hui，ZHENG Yong-gang，LIU Yue-xia.2005.The radiocarbon age of carbinized wood in Tianchi volcano，Changbaishan Mountains and its implication［J］.Seismology and Geology，27(1):83—88(in Chinese).

于红梅，许建东，赵谊.2007.长白山天池火山千年大喷发空降碎屑物的数值模拟［J］.地震地质，29(3):522—534.

YU Hong-mei，XU Jian-dong，ZHAO Yi.2007.A numerical simulation of tephra transport and deposition formillennium eruption of Changbaishan Tianchi volcano［J］.Seismology and Geology，29(3):522—534(in Chinese).

赵谊.2003.火山危险性和空降碎屑灾害的研究［D］:［学位论文］.安徽:中国科学技术大学.

ZHAO Yi.2003.Study of volcanic hazard assessmentand the risk of airborne substances［D］.Dissertation for the Doctoral Degree.University of Science and Technology of China，Anhui(in Chinese).

赵谊，张程远，席道瑛.2002.火山碎屑空降沉积的二维数值模拟［J］.地震地质，24(3):377—386.

ZHAO Yi，ZHANG Cheng-yuan，XIDao-ying.2002.2D-numerical simulation of dispersion of tephra fallout［J］.Seis-mology and Geology，24(3):377—386(in Chinese).

Bonadonna C，Ernst G G J，Sparks R S J.1998.Thickness variations and volume estimates of tephra fall deposits:The importance of particle Reynolds number［J］.JVolcanol Geotherm Res，81:173—187.

Bonadonna C，Connor CB，Houghton B F，etal.2005.Probabilisticmodeling of tephra dispersion:Hazard assessmentof amulti-phase rhyolitic eruption at Tarawera，New Zealand ［J］.JGeophys Res，110(B3):Art.No.B03203.doi:10.1029/2003JB002896.

Bonadonna C，Phillips JC.2003.Sedimentation from strong volcanic plumes［J］.JGeophys Res，108(B7):Art.No.2340.doi:10.1029/2002JB002034.

ColtelliM，Miraglia L，Scollo S.2008.Characterization of shape and terminal velocity of tephra particles erupted during the 2002 eruption of Etna volcano，Italy［J］.Bull Volcanol，70(9):1103—1112.doi:10.1007/s 00445-007-0192—8.

Dellino P，La Volpe L.1996.Image processing analysis in reconstructing fragmentation and transportationmechanisms of pyroclastic deposits:The case of Monte Pilato-Rocche Rosse eruptions，Lipari(Aeolian Islands，Italy)［J］.JVolcanol Geotherm Res，71:13—29.

Dellino P，Mele D，Bonaria R，et al.2005.The analysis of the influence of pumice shape on its terminal velocity ［J］.Geophys Res Lett32，Art.No.L21306.doi:10.1029/2005GL023954.

Folk R L.1974.Petrology of Sedimentary Rocks［M］.Hemphill，Austin，Texas.182.

Heffter JL，Stunder B JB.1993.Volcanic ash forecast transport and dispersion(Vaftad)model［J］.Weather Forecast，8:533—541.

Kunii D K，Levenspiel O.1969.Fluidization Engineering［M］.Wiley，New York.97.

Macedonio G，Costa A，Longo V.2005.A computermodel for volcanic ash fallout and assessment of subsequent hazard［J］.Comput Geosci，31:837—845.

Machida H，Arai F.1983.Extensive ash falls in and around the Sea of Japan from large Quaternary eruption ［J］.Jour Volcan Geother Res，18:151—164.

Machida H，Sugiyama S.1990.The recentmajor eruption of Changbai Volcano and its environmental effects［J］.Geographical Report of Tokyo Metropolotan University，25:1—20.

Muller G.1967.Methods in Sedimentary Petrology［M］.Hafner，New York.

Pfeiffer T，Costa A，Macedonio G.2005.A model for the numerical simulation of tephra fall deposits［J］.JVolcanol Geotherm Res，140:273—294.

Riley CM，Rose W Ⅰ，Bluth G JS.2003.Quantitative shapemeasurements of distal volcanic ash［J］.JGeophys Res，108(B10)，Art.No.2504.doi:10.1029/2001JB000818.

Russ J.1995.The Image Processing Handbook ［M］.CRC，Boca Raton，FL.674.

Sparks R S J，Bursik M Ⅰ，Carey SN，et al.1997.Volcanic Plumes［M］.Wiley，Chichester.

Searcy C，Dean K，Stringer W.1998.PUFF:A high resolution volcanic ash trackingmodel［J］.JVolcanol Geotherm Res，80:1—16.

Suzuki T.1983.A theoretical model for dispersion of tephra ［A］.In:Shimozuru D，Yokoyama I eds.，Volcanism:Physics and Tectonics.Arc，Tokyo:95—113.

Wilson L，Huang TC.1979.The influence of shape on the atmospheric settling velocity of volcanic ash particles［J］.Earth Planet Sci Lett，44:311—324.

MORPHOLOGICAL CHARACTERIZATION AND TERM INAL VELOCITY OF PUM ICE PARTICLES ERUPTED DURING THE M ILLENNIUM ERUPTION OF CHANGBAISHAN TIANCHIVOLCANO，CHINA

YU Hong-mei XU Jian-dong LIN Chuan-yong
(Institute of Geology，China Earthquake Administration，Beijing 100029，China)

The shape parameter of particles is an important parameter in the formula of the terminal settling velocity，but itwas usually assumed to be spherical or ellipsoidal without detailed study.According to themorphological characterization of the tephra particles erupted during the Millennium eruption of Changbaishan Tianchi volcano，we got some new recognition:The tephra particles consistmainly of pumice，which have irregular shapes，varying from very equant to elongate and from subrounded to angular.With decreasing of the particle size，the elongation of particles becomes significant，and the proportion of elongated particles increases from 15.02%to 47.5%.Moreover，the smaller the size of particles is，themore angular the shape of particles.An average shape parameter F=0.72 has been obtained through themorphological characterization of the pumice particles.The terminal velocity of the pumice particles，which were assumed to be spherical(F=1)，erupted during the Millennium eruption of the Changbaishan Tianchi volcano is about1.52 times the terminal velocity of the pumice particles of F=0.72，and the terminal velocity of the pumice particles，which were assumed to be ellipsoidal(F=0.5)，is about0.89 times the terminal velocity of the pumice particles of F=0.72.When the wind speed is taken to be 10m/s，the isopach map of tephra particleswith different shape parameters shows that the dispersal range expands with the decrease of the shape parameter F.The aforementioned results show clearly that the morphology of particles influences strongly both the terminal settling velocity and dispersal range，and hence should be fully considered when simulating tephra dispersion and forecasting disasters in the future.

pumice particles，shape parameters，terminal settling velocity，tephra dispersal model，Changbaishan Tianchi volcano

P317.3

A

0253-4967(2011)02-0440-12

10.3969/j.issn.0253-4967.2011.02.017

2010-09-12收稿，2010-11-22改回。

国家自然科学基金(40972209)和地震行业科研专项(20070827)共同资助。

于红梅，女，1981年生，中国地震局地质研究所博士研究生，主要从事火山学研究，电话:010-62009135，E-mail:yuhongmei188@163.com。