多重网格算法在地球物理电磁三维正演中的应用

李小康,王 伟,刘 磊

(1.中国地质大学 (北京)地球物理与信息技术学院,北京100083;2.中国地质大学 (北京)地球科学与资源学院,北京100083)

大地中电磁波的传播可以用麦克斯韦方程组和欧姆定律进行表述。在地球物理勘探一般用到的是1Hz左右的低频部分,光速波的幅值很小,并且波长大大超出研究域范围,因此扩散作用是主要的研究对象,大地电磁法和可控源电磁法应用的都是电磁波的扩散原理。

在二维条件下,电磁波传播问题可被简化为泊松型方程,方程可以使用直接法求解,如嵌套剖分[1];也可以使用迭代法求解,如多重网格法。而在三维条件下,直接求解法对于大尺度问题进行求解的成本太高,而迭代法就显示出其优势。

在求解线性方程组时,旋度-旋度运算所形成的大型零空间是一个很大的难题。为了避免求解零空间问题,一般通过亥姆霍兹分解将电场转为电位,得到泊松型方程组系。实际上,零空间的问题可以直接通过散度校正求解,或者通过划分小的局部子系统进行间接求解。本文选用后一种方法,用有限积分法对方程组使进行离散化,这一过程可以被看作在 Yee方案的基础上[2],引入了有限体积法。

多重网格法应用于三维电磁法正演问题,一般有两种思路,即单独使用多重网格法求解,或者是作为 Krylov子空间法的预处理过程使用。当多重网格法本身很难消除某种误差的情况下,一般使用后一种方案。本文对于以上两种方案的收敛性都进行了研究,并进行了一系列模型试算。进行正演试算的模型包括,理想状态下的垂直接触带模型,均匀介质中点电源模型和海洋环境盐丘模型。其中,对于网格拉伸对于算法收敛性的影响和解决方案,本文也进行了着重研究。

1 方法

1.1 方程离散化

角频率为ω的自由频率空间中,导电介质的麦克斯韦方程为:

ωμ0σ～- ¤E ×μ-1r¤ ×E=-ωμ0Js (1)式中,矢量 E(ω,x)表示相应角频率和位置上的电场分量,Js(ω,x)为电流源,σ～(X) =σωμrμ0,σ(X)为电导率,:r(X)为介电常数,μr(X)为磁导率,:0和μ0为真空中的值,使用SI单位制。由于地球物理勘探中所应用的频率在1Hz左右,那么除在空气中外,σ～(X)中的ω:0:r值可忽略不计。在后面算例中,我们针对地球物理模型取:r=1,而理想化模型中取:r=0。

下一步,在张量积笛卡尔网格中,使用有限积分法对方程组进行离散化。网格节点可以确定方形网格,电场分量取棱边上的均值,而磁场分量 H= (¤ ×E)/(ωμrμ0)通常被分配指向元胞的各个表面。这些分量可以形成节点位于原始元胞网格质心的派生网格,见图1。磁场分量的旋度可以被归到原始元胞的各个棱边,但原始元胞的各节点并不一定要位于派生网格的质心。

体积与电导率的乘积为:

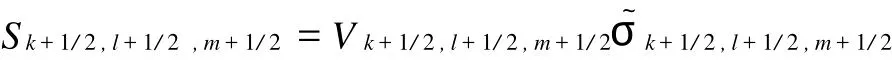
以棱边 (k+1/2,l+1/2,m+1/2)处的分量为例,求平均过程为

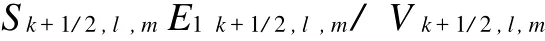
Vk+1/2,l,m是两个派生元胞叠加的部分,其中包含了棱边 (k+1/2,l,m),也是四个原始元胞的公共边。为了运算方便,我们针对 Sk+1/2,l,mE1k+1/2,l,m进行研究。

由电场旋度求取电场分量,需要求元胞各表面处的 1/μr,即在派生元胞棱边处对 1/μr求平均[4]。由于物性参数值在每一个元胞中为常数,这个过程也就是针对平面两侧元胞中的1/μr按体积求加权平均。有时为了使模拟更加精确的逼近于真实情况,往往设定元胞内部的物性也存在变化,取平均的过程就不能使用简单的体积加权。这样的情况较复杂,本文暂时不进行考虑。

对于电流源Js的各个分量可以按照与电场分量类似的方法分配到各个棱边上,各个分量大小分别为派生元胞各个表面的均值,磁场分量的旋度处理方式与之相同。如果将Js通过派生元胞一个表面的分量的积分与其所在的棱边长度相乘,那么就得到了电流源分量与双重棱边体积的离散化结果。

经过这样的离散化,最终的解对于常系数具有二阶精度[5],即便系数在跨域过程中发生变化,精度仍然能够保持,除非发生的变化不连续。因为在上述情况下,一般会导致解中存在一阶的误差。

1.2 多重网格法

Feigh曾介绍各类多重网格方法[6],本文网格粗化使用八个相邻细网格元胞自然粗化为一个粗网格元胞的方法,引入将物性参数与相应元胞体积的乘积用于约束。为了约束残差,共引入两个约束算子。

第一个等于在粗网格双重棱边体积内包含的细网格双重棱边体积部分的缩放比例合适情况下,给定棱边处的粗网格体积中包含的所有双重棱边体积的积分。如果元胞的宽度固定,那么这个值

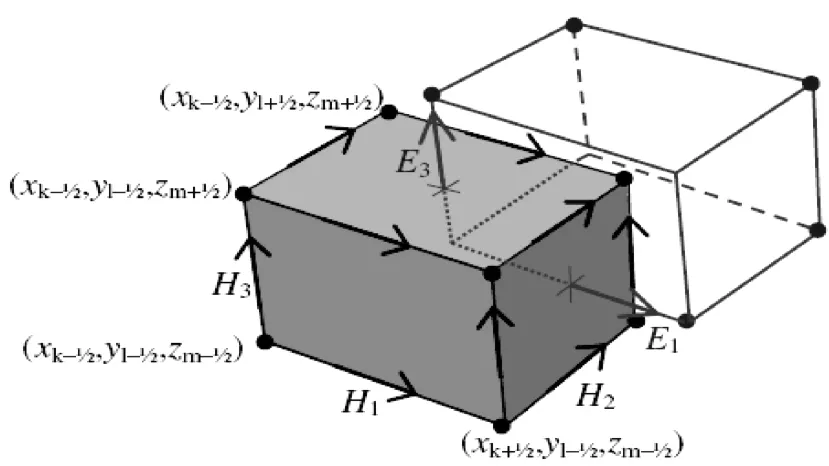
图1 原始元胞 (空心)与派生元胞 (实心)示意图

物性参数在每个元胞中为常数,要得到电场分量所在各边上的电导率σ,需取均值。在两个派生元胞共享的平面上,应当使用面积平均[3],下面详述取均值的过程。

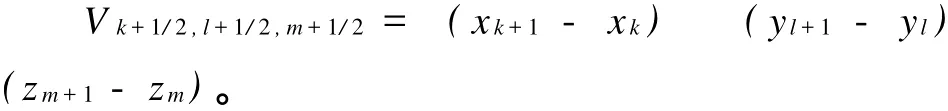
将一个 Nx×Ny×Nz的网格的节点分别指定为xk(k=0,…,Nx),yl(l=0,…,Ny)和zm(m=0,…,Nz)。若某个元胞的体积表示为:则减少到全权重。为了对其进行详细阐述,首先考虑一种较为简单的情况,有一个 Nx×Ny×Nz的网格,其中 Nx=Ny=Nz=2M,M≥1。假定按照网格节点 xk(k=0,…,Nx),yl(l=0,…,Ny)和zm(m=0,…,Nz)中隔点对网格进行粗化,粗化后的网格节点为 (x2K,y2L,z2M)其中K=0,…,Nx/2,L=0,…,Ny/2,M=0,…,Nz/2。以残差 r的第一分量为例,表述约束因子。将残差与双重棱边体积相乘,其分量与相应的电场分量分布在相同的棱边上。第一级粗网格的残差分量就是,上标2h指示网格的粗化值。令粗网格中的指标 K与细网格中存在k=2 K的关系,同样的l=2L,m=2M。那么该分量的约束条件为:

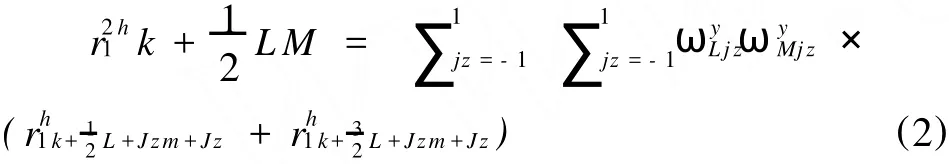
其中

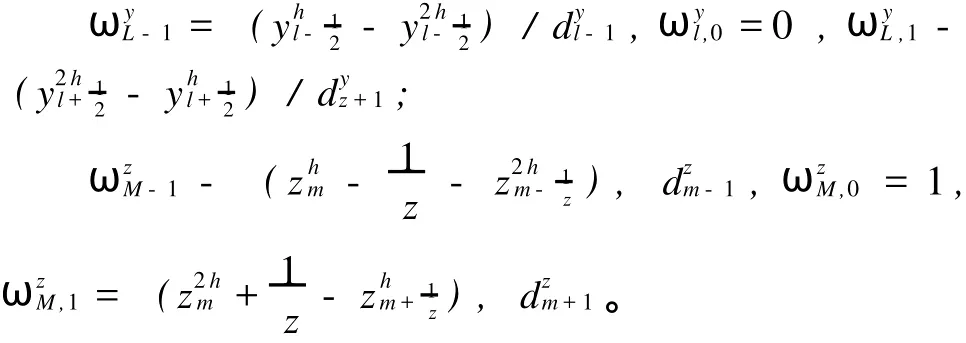
第二个约束因子,等于在双重棱边体积缩放比例合适的情况下,粗网格棱边上细网格残差的

为了将粗化网格时电场分量的校正值进行延拓,在分量方向上分段使用常数插值,在垂直于分量的平面上使用线性与双线性插值,这也与式(2)的共轭方程相同。在编序过程中使用对称体Gauss-Seidel(SBGS)法,作为网格循环过程的平滑器和SBGS松弛的一个步骤,每个循环进行两次后平滑处理。而当多重网格充当预处理器时,仅需作一次网格循环。

2 模型正演计算

2.1 垂直接触带模型

基于本征函数的垂直接触带问题是经常用于算法测试的模型,此处对其稍作修改,使用理想导电边界条件。设研究域为,Ω= [0.2π]3m3,ψ=sinkxsinlysimy,其中 k、l、m为正整数。精确解为:

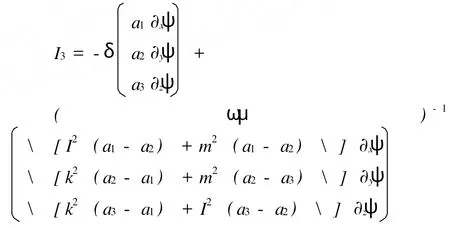
E1=α19xψ,E2= α29yψ,E3=α39zψ (3)

设研究域Ω中有,Ω1(z<π)和Ω1(z>π)。在Ω1中σ=σ0+σ1(x+1) (y+2) (z-π)2,在Ω2中σ=σ0,同时设:r=0,μr=1,ω=106H z。其他参数设置为α1=α2=-2V,α2=1V,k=l=m=1,σ0=105/m,σ1=15/m。由于模型中使用理想导体边界条件,基于正弦函数,则电场的切向分量在边界处为零。电流源表达式可写为 Ie=-δE+¤× (ωμ)-1¤×E,将精确解式 (3)代入该式得到:

同时,将三个方向上网格剖分单元数量分别设为 Nx=Ny=Nz=N,对于每套网格分别使用两种迭代方法,即单独使用多重网格迭代 (M G)和多重网格预处理后的双共轭梯度稳定法 (bi),设定当残差对于零解的范数由初始值下降到10-8数量级时,停止迭代,结果见表1。

通过2范数和最大范数对误差进行检查。如果网格有 Nx×Ny×Nz个元胞,网格节点可表示为(xk,yl,zm),k=0, …,Nx,l=0, …,Ny,m=0,…,Nz,第一电场分量的2范数为:其他分量的范数与之类似。解的误差为:相对误差为:最大范数为:

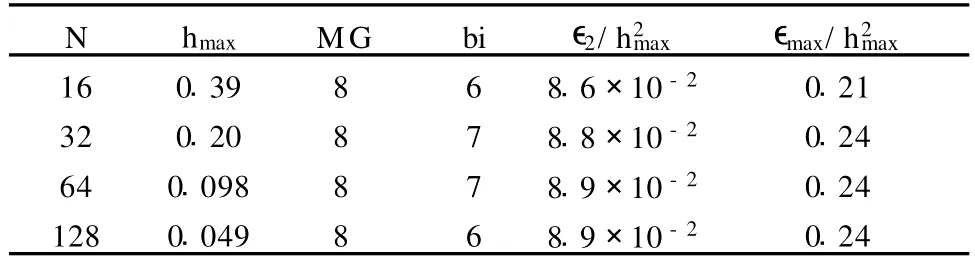
表1 垂直接触带模型迭代次数及误差统计

由表1可见,此时多重网格法的收敛性与网格尺度无关。双共轭梯度稳定法的迭代次数较少,但是由于额外的CPU时间和存储要求,使得该方法变得十分不合算。例如,对于1283尺寸的网格而言,双共轭梯度稳定法6次迭代与单独使用多重网格算法8次迭代相比,效率仅高10%。通过对误差的分析,确定了数值解的二阶精度。

接下来对网格拉伸的效果进行研究,网格拉伸是指从坐标原点沿坐标轴开始向外进行网格剖分时,按照1+α的比率将剖分尺度逐步放大的处理,等距网格中α=0。针对拉伸系数为α=0.04的网格剖分模型计算结果见表2。通过对比,显然可以发现此时多重网格法收敛性对于网格剖分的独立性消失,而双共轭梯度稳定法的优势也显现出来,因为该方法可以对收敛较慢的分量进行有效地处理。由表中误差检测的结果:2和:max可知,两种方法的解仍具备二阶精度。

表2 α=0.04时垂直接触带模型计算结果

综上可知,对于电流源问题,网格拉伸未必会起到好的效果,至少一定程度上会影响迭代过程的收敛速度,在未来的研究过程中应当引起注意。

2.2 均匀介质中电流源模型

下面对更加贴近实际的匀质地层中的点电流源问题进行讨论。模型参数设置为研究域设定成尺寸为[-1,1]×[-1,1]×[-1,1]km3的立方体区域,点J3= (0.01)δ (x)A/m2电流源放置在原点。首先采取等距网格对模型进行离散化,剖分单元设置为Nx=Ny=Nz=N,然后使用功率拉伸网格对两种迭代法的表现进行对比。为了电流源表达式进行离散化,这里使用了三线性插值共轭法。迭代停止条件是数值解对于精确解残差的l2范数由初始值降至10-8数量级,该问题的精确解由Ward给出[7]。尽管理想导体边界条件不适用于该问题,但是只要将边界置于据电流源足够远处,在求解时仍然可以使用。由于精确解在源处存在一个r-3的奇异值,所以无法通过网格加密降低误差。点电流源可以由有限长线源代替,线源的长度则取决于源所在的棱边长度。在本算例中,电源的位置恰好位于节点处,并恰好可以由节点上方和下方的棱边表示。上述棱边长度的改变对近区的电磁场影响较大,有可能使最终的解失去二阶精度。而远区场则不受源的这些细节影响,只取决于源的总体性质。通过测量立方体 [-250,250]3m3之外的误差,得到的计算结果见表3～表5。

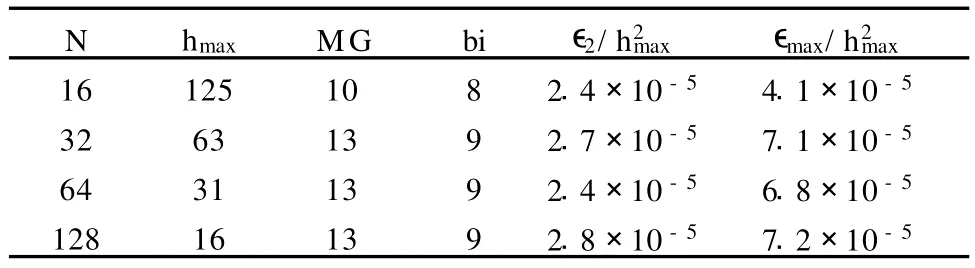
表3 点电流源模型固定网格的迭代次数及误差统计

表4 时点电流源模型计算结果

表5 时点电源模型计算结果

可见在网格无拉伸的情况下,迭代效率相当高,而对网格进行超过几个百分点的拉伸后,收敛性就开始急剧下降。

2.3 海洋环境盐丘模型

进一步地为了构建一个更加贴近实际的地下半空间模型,对已有的SEG/EA GE的盐丘模型[8]进行一定修改。修改前的盐丘模型,是设计用来模拟人工地震波传播,其中构建了一个被沉积岩所包围的复杂盐丘体,设计海水深度120m,模型尺度设置为13500m×13480m×4680m。由于在实际的海洋可控源电磁勘探 (CSEM)中,海水深度比原模型设置要深,因此首先需要把模型中海水深度加大到500m。然后由于需要进行电磁三维正演,因此物性参数中的速度相应由电导率代替,即将海水中波速1500m/s替换为电导率10/3 S/m,盐丘中波速4000m/s替换为电导率1/30 S/m,而深度大于3956m处的基底岩层电导率设为500 S/m,沉积岩中的电导率由波速 v(单位为m/s)确定[9],设为空气中的电导率设为10-10S/m,最后将这些电导率参数填入通过双曲余弦拉伸的新网格。其中水平方向的网格剖分与原模型相同,设定z范围为 (-5000m,5000m)。在海底,在y=0m处沿 x方向由 x=4000m至x=10000m之间,按照200m间距设置接收机,深度范围设定在605m至625m,模型的示意图见图4。为对模型进行离散化,需计算相应的元胞均值,频率为

源位于 (x,y,z)= (6400m,6500m,500m)与 (x,y,z)= (6600m,6500m,500m)之间。

针对1283剖分网格进行计算的结果见表6,网格拉伸由双曲余弦函数控制,其中最小的单元格宽度为hmin,相邻两网格之间的尺度比的最大值用表示。正演计算过程中,多重网格还是作为双共轭梯度稳定法的预处理步骤使用,同样地,网格拉伸对于迭代性能的影响也做了进一步研究。

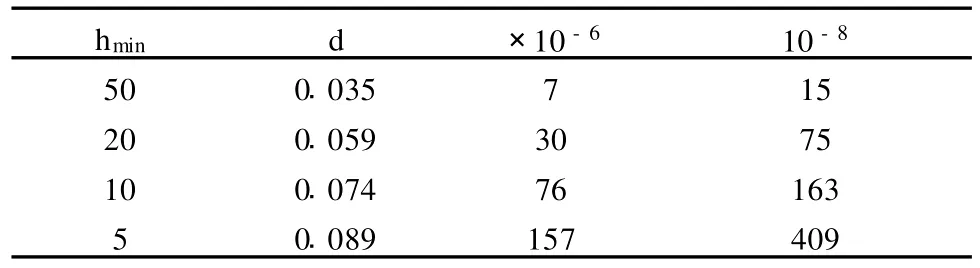
表6 使用多重网格预处理的bicgstab法迭代次数

4 结论与思考

本文研究了针对在张量积笛卡尔网格中的电磁扩散方程有限积分离散化技术的多重网格法,进行了一系列模型试算,着重观察了等距网格和拉伸网格剖分对收敛性的影响。网格拉伸会引起离散方程的各向异性的特征,这一直以来都是多重网格法比较难以解决的问题,未来的研究中可以考虑以下几种解决方案:

1)Krylov子空间法可以用于消除导致收敛变慢的解分量。尽管本文使用双共轭梯度稳定法取得了一定效果,但是该方法起到的作用有限。

2)线性松弛法,例如对称线性 Gauss-Seidel法,可以用来消除网格拉伸带引起的各向异性趋向。对于三维问题,可以考虑使用平面松弛法,但是计算成本会提高。

3)半粗化处理也可以达到同样的效果。在标准的多重网格迭代流程中,每次仅对一个方向进行粗化。使用对网格所有方向同时进行粗化的算法,那么与之相关的时间成本增加可以通过后续计算效率的提高得以弥补。

4)通过权重约束因子和延拓因子的控制,可以大大降低物性参数变化带来的负面效果[10]。

5)可以借鉴计算机技术中解决等距网格中局部细化问题的方法。这一算法应当可以在局部使用较细的网格,同时保证算法的收敛速度,当然这一算法的编程实现更为复杂。

以上提到的几种思路,必然会使得多重网格迭代的计算过程更为复杂,下一步需要做的就是从中选出效率或者说“性价比”最高的一种解决方案。

[1] George A,Liu J.Computer Solution of Large Sparse Positive Definite Systems[M]. Prentice-Hall,Englewood Cliffs,1981.

[2] Yee K.Numerical solution of initial boundary value p roblems involving Maxwell’s equations in isotropic media[J].Antennas Propag,1966,16:302-307.

[3] Clemens M.,Weiland T.Discrete electromagnetism with the Finite Integration Technique[J].Prog Electromagn Res(PIER),2001,32:65-87.

[4] van Rienen U.Frequency domain analysisof waveguidesand resonators with FIT on non-orthogonal triangular grids[J].Prog Electromagn Res(PIER) ,2001,32:357-381.

[5] Monk P,Süli E.A convergence analysisof Yee’s schemeon non uniform grids[J].SIAM J,1994,31:393-412.

[6] Butler DK.Potential Fields Methods for Location of Unexploded Ordnance[J].The Leading Edge,2001,20(8):890-8951.

[7] Ward S,H Hohmann.Electromagnetic theory for geophysical applications.Society of Exploration Geophysicists,Tulsa.Nabighian,M.N.(ed.)Electromagnetic Methods in Applied Geophysics—Theory,1987,1(1):131-311.

[8] Aminzadeh F,Brac J,Kunz T.3-D Salt and over thrust models[J]. Society of Exploration Geophysicists,Tulsa,1997.

[9] Meju M.A.,Gallardo L.A.,Mohamed A.K.Evidence for correlation of electrical resistivity and seismic velocity in heterogeneous near-surface materials[J].Geophys.Res.Lett.,2003,30(7):1373-1376.

[10] Wesseling P.An Introduction to Multi-grid Methods[M].Wiley,New York,1992.