非成像光学应用于LED照明的研究

李澄 李农

(北京工业大学城市照明规划设计研究所，北京 100124)

1 引言

自从1879年，托马斯.A.爱迪生发明了世界上第一盏白炽灯，人类就进入了照明的另一个新时代——电气照明时代。从1962年至今，发光二极管(LED)技术历经了40多年的飞速发展，半导体光源应用于照明领域的两大瓶颈:光效与成本问题也在迅速得到改善，目前大功率LED的光效已超过传统的室内照明光源 (白炽灯、荧光灯)，因此照明领域已普遍认为LED照明光源是继火光照明、白炽灯、荧光灯、气体灯之后出现的第四代新型绿色固态冷光源，由于LED具有安全节能、长寿命、绿色环保、色彩丰富、抗震抗冲击、微型化、响应速度快等显著优点，如能完全替代传统光源进行照明，它将成为人类照明史上继白炽灯、荧光灯之后的又一飞跃，其经济和社会意义巨大［1］。最早的照明设计中，人们一般是采用根据经验的实测方法进行的，即首先凭借经验做一个实际的模型，之后看看这个模型是否符合设计要求，实测法虽然比较准确，但只有在照明系统制造出来以后才能进行，一旦发现其光学特性不能满足要求，只能重新设计和制造灯具，这不但增加了人力和物力的消耗，而且延长了灯具的设计和制造周期［2］。

随着应用光学的发展，人们逐渐掌握了球面透镜、非球面透镜、各种基本形式的反射器的设计原理，通过器件及其组合达到设计目标。这一时期，主要采用的是成像光学的设计方法，设计者通常将类似的能量收集或分配问题当作是一种具有很大数值孔径的成像光学问题。通过这种方法设计的光学系统通常并不能取得理想的能量收集率。但设计这类光学收集器的目标是取得或接近取得理论数值的最大极限。那么如何能够得到理想的器件呢?

20世纪60年代中期，在传统的成像光学设计方法的基础上逐渐发展出了一系列新理论，并被应用于上述能量收集和分配的方法中。这种采用新理论的光线收集器件被命名为非成像收集器(nonimaging concentrators)。这种新发展出来的光学系统不同于传统的成像光学系统，其具有一些导光管或具有很大畸变的成像光学系统的性质。对于这些非成像系统的设计和理论的研究为几何光学的发展开拓了很多新的思想和理论。由于非成像收集器重视的是能量的分配，而不是清晰的成像，所以这种器件可以很好地应用于照明领域。在照明领域中，光源发出的光线一般来说具有较宽的角度 (例如LED发出的光线是朗伯分布，白炽灯等光源发出的光线是球形分布)，因此可以使用非成像光学器件对这些光线进行高效率的准直。故采用非成像光学设计原理工作的照明器件可以很好的完成设计目标。

目前，非成像光学理论［3］的体系和 LED二次光学设计技术内容较为松散，国内阐述这方面设计方法的文献资料缺乏系统性、完整性。本文的目的就是将非成像光学的一些主要基础理论做系统性的归纳、整理、阐述，在此基础上较完整、系统地介绍了一些LED灯具的二次光学配光器具的设计方法。

2 非成像光学的基本概念和理论

一般来说，非成像光学的基本理论框架体系可概括为两大概念 (能量收集率与光学扩展量)、三大原理 (边缘光线理论、费马原理和马吕斯—杜宾定律)以及几何光学的四大基本定律 (光的直线传播定律、光的独立传播定律和光的折射、反射定律)，它主要研究两类问题，第一类问题一般被称为“光束耦合问题” (bundle-coupling)，该问题的关键在于如何将光线收集到目标接收器上并同时获得最大收集率。非成像光学研究的第二类问题通常被称为“指定辐射度”或“指定光强分布”(prescribed irradiance)问题，该类问题主要被应用在照明领域。在本文中，主要考虑第二类问题。例如，在汽车照明或室内照明等领域，通常使用的光源是灯泡或LED芯片，并且目标表面远离光源，且目标表面要求实现指定的光强分布。在非照明领域，也有一些类似的应用，例如，用于室内通信的广角红外接收器，当接收器的灵敏度被指定时，为补偿桌面上多个发射器的不同连接距离，接收器灵敏度的作用就与照明设计中光强分布的作用类似了。

2.1 能量收集率 (concentration ratio)的概念

由于非成像光学注重的是能量的分配，当建立一个如图 (1)所示的非成像器件的模型时可以看到，它具有一个入射孔径面积为A的平面和一个出射孔径面积为A'的平面。假设它的出射孔径面积A'可以让所有的光线均透过它出射，那么通常将器件入射光束的面积与器件出射光束面积的比值C定义为能量的收集率。

对于2D系统来说该能量的最大收集率为C2D=1/sinθ，而对于一个旋转对称的3D系统来说能量最大收集率为目前能量收集率的概念被普遍用于非成像光学系统的评估上。

2.2 光学扩展量 (ètendue)的概念

光学扩展量的概念源于光能在非成像光学系统中的传递。当光能在传递过程中无损失时，光通量的传递可表示为='。根据光亮度Lθ，光强朗伯余弦分布Iθ和立体角ω的公式，一个光强成朗伯余弦体分布的LED光源，可以按下式来定义它的光通量，假设式中dS为LED光源中的一微小物面，其光亮度为Lθ，故该微小物面发出的光通量为，

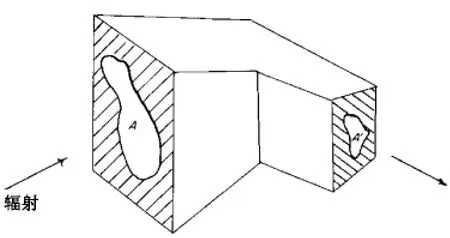
图1 能量收集率的概念

对式 (1)进行化简并带入无损光通量传递公式='，便可得到式 (2)，式中 U为法线与主光线的孔径角。

考虑到空间中光线亮度的传递问题，可化简式(2)，得到式 (3)，

该式即为光学扩展量的数学表达式，由此可以很容易地得到光通量与光学扩展量 (ètendue)的关系式，

ètendue出自法语，原意为几何量值 (geometrical extent)，目前没有统一的中文译名。故笔者根据其意译为光学扩展量。它是光学系统中的一个重要指标，在非成像光学中，该值越大，意味着传递的光能越多。利用光学扩展量守恒的概念，便可进行自由曲面配光器件设计公式的推导。

2.3 非成像光学的三大原理

边缘光线原理 (The edge-ray principle)，费马原理 (Fermat’s principle)和马吕斯—杜宾定律(the theorem of Malus and Dupin)是非成像光学的三大基本原理。其中，费马原理定义了“光程”(optical path)的概念，这也是马吕斯—杜宾定律中提出的“波前”(wave front)概念基础，同时马吕斯—杜宾定律也表明“光线束在各向同性介质的传播过程中，始终保持着与波面的正交性。”该定律是非成像聚能器 (Compound Parabolic Concentrator，CPC)设计的重要理论基础。边缘光线原理 (the edge-ray principle)最早被作为假设引入到非成像聚能器的设计中，后来直到1986年，才由 Mińano提出相关的数学证明。基本内容就是:对于以最大角度入射到非成像光学器件内部的光线，在经过一次反射或折射后必定会被引导到聚能器出射口边缘，出射光线依然是聚光器出射口处出射角度最大的光线。该原理意味着在非成像光学设计中，仅需考虑边缘位置的光线，而不需要考虑太多的其他内部光线。

2.4 几何光学的四大基本定律

几何光学目前已被应用于大部分的光学系统设计中，无论是非成像光学还是成像光学系统，均需遵守几何光学的基本理论，该内容可在很多书籍文献［6］中查到。光的直线传播定律主要说明 “在各向同性的均匀介质中，光沿直线传播”;光的独立传播定律说明“从不同的光源发出的光束以不同方向通过空间某点时，彼此互不影响，各光束独立传播”;当光线经过两种均匀介质分界面时，遵循折射定律和反射定律。反射定律的概念是“入射光线、反射光线和投射点法线三者在同一平面内，入射角和反射角二者绝对值相等、符号相反，即入射光线和反射光线位于法线的两侧”。当光透过透明介质时遵守折射定律，它的内容是“入射光线、折射光线和投射点法线三者在同一平面内，入射角的正弦与折射角的正弦之比与入射角的大小无关，而与两种介质的性质有关。对一定波长的光线，在一定温度和压力的条件下，该比值为一常数，等于折射光线所在介质的折射率n'与入射光线所在介质的折射率n之比”。

反射定律、折射定律的矢量表达式由Ries等人自1993—2002年连续发表的多篇相关论文［7～9］而提出。它采用一个二阶的偏微分等式 (Monge-Ampere Type Equation)，对“波前”进行描述，同时自由曲面的法向量、曲率等也可以被描述成对应的微分方程，将其代入下面的向量形式的折、反射定律公式，即可得到相应的偏微分方程组。

3 应用非成像光学进行LED二次配光器件的设计

3.1 LED光源光强分布的特点

对于一个大功率LED芯片来说，LED发光管内的光学结构通常由芯片和硅胶 (或PC)透镜构成。硅胶透镜的几何形状决定了LED出光后的空间光强分布。通常来讲按照光强的分布特点，光源可分为三种类型:朗伯分布光源、均匀分布光源以及受限朗伯分布光源。

对于LED芯片，一般来说，芯片发光面经过PC透镜 (也有硅胶透镜)出射光线的角度分布符合朗伯余弦定律，即表示为［10］

式中θ为该方向与平面法向的夹角，I0为法向最大光强。该光强分布在LED的自由曲面透镜设计中被广泛应用。

3.2 复合抛物聚能器 (Compound Parabolic Concentrator，CPC) 的设计

1966年，苏联的B.K.巴兰诺夫和G.K.苗尔尼可夫，美国的H.海一英特伯格和R.温丝东以及1967年德国的M.帕洛克先后独立地提出了一种用于高能物理实验研究中的辐射探测器，其特点是可将探测器开口面上的包含在设计接受角内的透射辐射全部收集到核心的接受元件。随后，这种最初用于高能物理收集辐射的器件被先后用于太阳能收集和照明领域，并取得了良好的效果。根据数学推导可以证明该系统具有最大能量收集率。根据式(7)，利用公式 (8)，便可完成一般CPC的设计。

其中:

式中 收集角θi为入射光线角度，a'为入射孔径尺寸，a为出射孔径尺寸。关于CPC的设计，根据不同的需要，可以有几类变形。例如利用折射率公式可以设计实心CPC。利用两方向收集角的不同设计矩形CPC。图2是这几种CPC的设计实例。该类配光器件已被广泛应用于LED射灯、LED投光灯的二次光学设计中。

图2 不同种类的CPC设计及其照度分布

3.3 自由曲面配光器件的设计

利用非成像光学理论中的光学扩展量守恒概念(式2)以及矢量形式的折、反射定律 (式5)，便可以设计照度均匀分布的自由曲面透镜。目前最为常用的自由曲面设计方法主要有两种:数值优化法(Numerical OptimizationMethod)［12］和直接法 (Direct Method)［11］。数值优化法的设计首先需要寻找一个初始结构，之后根据这个结构，选择相应的参数进行优化。若初始结构选择有误，则所有的努力将前功尽弃。使用该方法设计自由曲面透镜需耗费大量的时间。直接法发展于20世纪90年代，使用该方法可以快速的求取自由曲面的面型。但该方法需要较深的数学功底。使用直接法进行自由曲面设计时，需要明确光学系统的初始条件，即明确光源的光强分布函数以及预期在照明目标面上的照度分布。通过直接法设计的自由曲面，可将光源的光强分布与照明目标面的照度分布加以匹配。故通过编程使用直接法设计自由曲面可使设计速度加快，设计出的自由曲面配光器具仅需进行很少的修改就能应用于实际。

使用直接法设计的自由曲面主要有旋转对称形配光和非旋转对称形配光两类器件。如图3所示。旋转对称型配光器件主要采用数学建模的方法，利用折、反射定律和光学扩展量守恒原理建立常微分方程，之后采用数值计算方法生成二维曲线函数，例如关于 (x，z)方向的函数再经过绕轴 (z轴)旋转360°而成［13］。非旋转对称形器件的设计同样是建立数学模型并利用折反射定律，但它建立的是一个二阶拟线性的偏微分方程。该方程的具体形式可参看相应文献［14］。图3设计了两种形式的配光器件，并在图中给出了它们的照度分布。采用该方法设计的自由曲面配光器件在LED灯具设计中具有重要的应用前景。

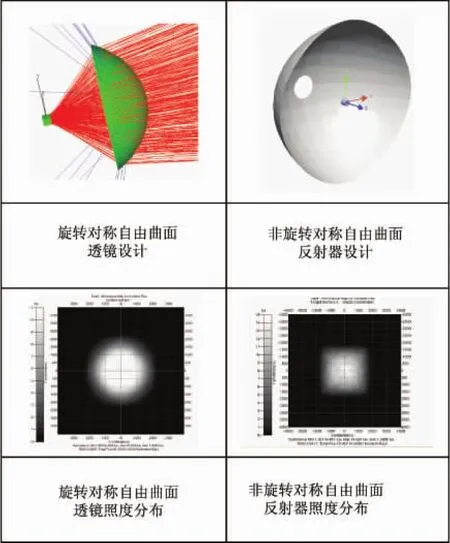
图3 自由曲面配光器件设计及其照度分布

4 展望

本文的所有研究工作都是围绕如何对LED的光强进行二次再分配并将其应用于照明领域而展开的。随着LED光源光效的不断提高和价格的不断下降，LED光源已经被越来越多的应用于照明的各个领域。众所周知，LED要应用于照明领域就不可避免的要解决好三个最主要的问题:①如何解决它的配光问题，使其的光分布达到目标照明面的要求;②如何解决好散热问题，使其应用的时候不会因为过热而损伤光源寿命;③如何解决好驱动电源问题，使其兼顾高效率和高功率因数。这三个问题在LED照明灯具的设计中往往是既相互联系又相互制约。做好LED灯具配光器件，充分发挥功率型LED的优势，对于加速中国半导体照明产业的发展具有举足轻重的意义。

［1］Song.Lee.Analysis of light-emitting diodes by Monte Carlo photon simulation.Applied Optics，2001.40(9):111 ～113.

［2］杨乐.关于LED应用于照明的研究和设计.2005，浙江大学硕士学位论文.

［3］P.A.Davis.Edge-ray principle of nonimaging optics［J］. J.Opt.Soc.Am.A，1994，11(4):1256～1259.

［4］Winston，R.，and Enoch，J.M.(1971).Retinal cone receptor as an ideal light collector.J.Opt.Soc.Am.61，1120～1121.

［5］Harald Ries，Narkis Shatz，John Bortz，and Wolfgang Sprikl，Performance limitations of rotationally symmetric non-imaging devices，J.Opt.Soc.Am.A.

［6］张以谟.应用光学.电子工业出版社.2008年8月:1(2):4～6.

［7］H.Ries and R Winston.“Tailored Edge-Ray Reflectors for Illumination.” J.Opt.Soc.Am.A 1260 ～ 1264(1994).

［8］H.Ries.“Tailoring Freeform Lenses for Illumination”.Proc.of SPIE 4442，43～50(2001).

［9］H.Ries.“Tailored Freeform Optical Surfaces.”J.Opt.Soc.Am.A 19，590－595(2002).

［10］D.Wood.Optoelectronic semiconductor devices［M］.Prentice Hall International，UK，1994.

［11］W.J.Smith，E.Betensky，and D.Williamson，et al.“The Past，Present，and Future of Optical Design”.SPIEOSA 6342，(2006).

［12］B.A.Jacobson and R.D.Gengelbacb.“Lens for Uniform LED Illumination:an Example of Automated Optimization Using Monte Carlo ray-tracing of an LED Source”.Proc.of SPIE 4446，121～128(2001).

［13］李澄，李农.一种用于均匀照明的 LED透镜设计方法.照明工程学报，2010，21(3):46～49

［14］Ding Yi， Gu Peifu. Freeform reflector foruniform illumination［J］.Acta Optica Sinica，2007，27(3):540～544.

［15］丁毅.顾培夫.实现均匀照明的自由曲而反射器 ［J］.光学学报，2007，27(3):540～544.