导引头伺服系统预定回路Anti-W indup设计
2011-12-03陈峻山陆涓涓
张 艳, 刘 扬, 陈峻山, 陆涓涓
(1.海军驻上海地区航天系统军事代表室,上海201109;2.上海无线电设备研究所,上海200090)
0 引言
伺服系统是雷达导引头的重要组成部分,根据导引头信号处理机提供的指令完成预定天线指向、隔离弹体扰动、跟踪目标和形成指令信号等功能[1]。预定回路完成天线指向预定功能,按照发射前提供的预定角信号或视向预定角信号,将导引头天线预先对准目标或前置一个角度,系统对其稳态精度、过渡过程的要求都很严格[1]。
作为一个典型的位置控制系统,预定回路可以按照经典控制理论的频域方法设计控制器,但由于实际系统中存在的多种非线性特性,必将影响线性控制器的性能。其中,最为显著的是饱和非线性会引起的控制器W indup(积分饱和)问题,需要设计Anti-W indup(抗积分饱和)控制器进行补偿[2]。
本文以某雷达导引头伺服系统的预定回路为研究对象,针对由饱和非线性引起的W indup问题,设计两种A nti-W indup控制器进行补偿;最后通过数字控制器实现补偿算法,并通过实验测试验证其控制效果。
1 回路Windup问题
1.1 回路模型
为确保系统静态动态性能,预定回路采用双环路结构:内环由测速机构成速度反馈回路,完成对电机速度的控制,外环由电位器构成位置反馈,完成对机构位置的控制,预定回路结构框图如图1所示。

图1 预定回路框图
图中,R为预定角;E为角误差;Ωr为参考角速度;U为驱动电压;Ω为电机角速度;Γ为天线指向角;G m(s)为电机传递函数;G l(s)为机构传递函数;K为测速机反馈系数;C v(s)为速度环控制律;Cp(s)为位置环控制律。
回路的控制对象为电机和机构组成的机电驱动机构,文献[3]对其这类驱动特性的建模进行了讨论,提出了刚性连接模型和弹性连接模型的两种建模方法,理论分析和试验测试表明,对于位标器的驱动特性,弹性连接模型更能准确描述系统特性。按弹性连接模型建模,得到电机和机构的传递函数如式(1)、式(2)所示。
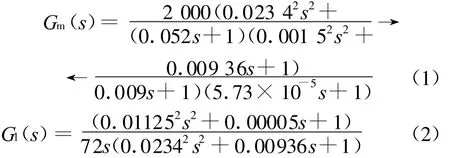
按照频域设计方法,设计测速机反馈为
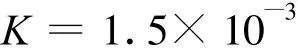
速度环控制律为

位置环控制律为

1.2 W indup问题
图1中sat(s)表示回路的驱动电压饱和特性,u和u⌒分别为饱和非线性之前的目标控制电压和饱和非线性之后的实际输出电压,它们之间的关系如式(3)所示。

由于回路中包含积分环节,这使得回路会产生饱和非线性带来的Windup问题。图2为考虑了加入饱和非线性后的回路模型对不同幅值阶跃信号的响应。
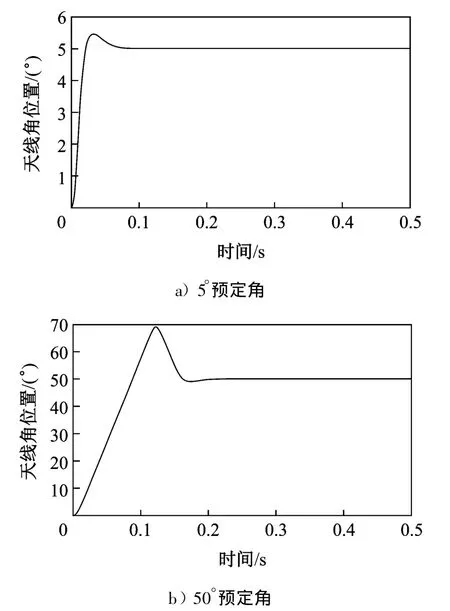
图2 含饱和非线性回路模型阶跃响应
从图中可以看出,当系统作小角度位置预定时,回路工作在线性区,饱和特性对系统没有影响;当系统作大幅度的位置预定时,饱和非线性造成回路性能严重下降,超调变大,调节时间变长,出现W indup问题。回路需要设计Anti-W indup控制律对饱和非线性进行补偿。常用的A nti-W indup设计有基于饱和控制的Anti-W indup设计和基于滤波器的A nti-W indup设计[4]。
2 Anti-W indup控制器设计
2.1 基于饱和控制的Anti-W indup设计
基于饱和控制的 Anti-W indup设计通过对线性控制施加饱和限制,避免驱动器出现饱和现象,从而消除W indup现象,文献[5]证明了该方法的稳定性。根据回路的驱动饱和特性选择饱和限制参数,在位置环控制律C p(s)加入饱和限制,修正后的位置环控制律如式(4)所示。
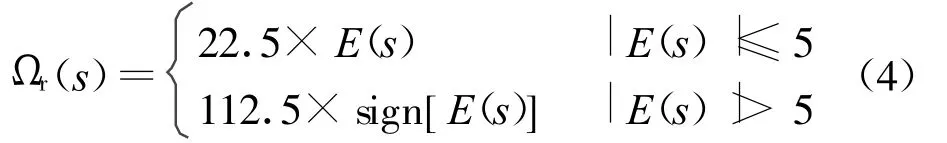
加入饱和控制后,回路的大信号阶跃响应仿真结果,如图3所示。
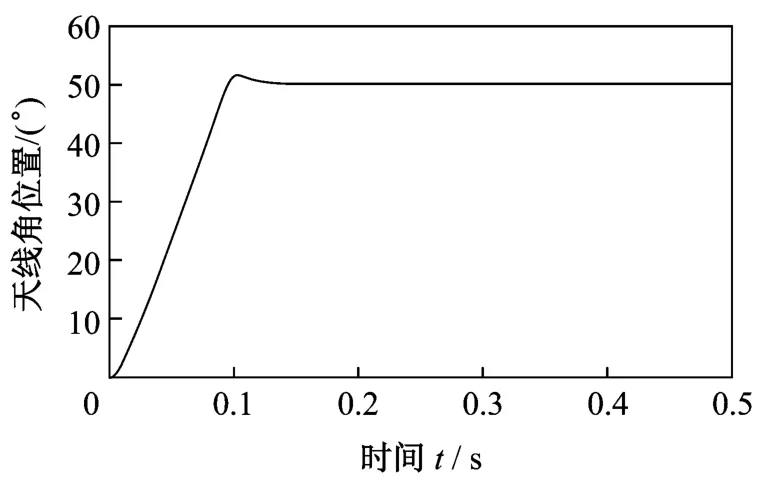
图3 基于饱和控制的Anti-W indup阶跃响应
从仿真结果中可以看出,采用基于饱和控制的Anti-W indup设计后,回路的大信号阶跃响应超调降低,调节时间减小,回路性能得到改善。
2.2 基于滤波器的Anti-W indup设计
基于滤波器的A nti-W indup控制方法由基于内模控制结构的Anti-W indup方法改进而来[6],使其更适应传统的反馈结构的控制系统,其控制方法如图4所示。

图4 基于滤波器的Anti-W indup控制
图中,F(s)为Anti-W indup补偿环节,根据饱和前后控制电压U和U⌒的差值,对控制量进行补偿,减小饱和非线性对回路的影响。
文献[7]给出了该方法的稳定性分析,文献[8]证明了在饱和非线性存在的条件下,该方法可以使系统性能达到最优,通过合理地选择F(s),可以有效地提高系统性能,并给出了F(s)的设计原则。按照文献[8]给出的设计原则,结合位标器预定回路模型参数,设计Anti-W indup补偿环节如式(5)所示。
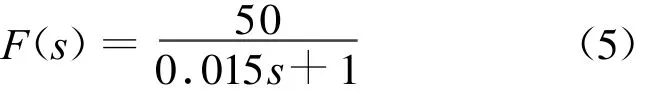
Anti-W indup补偿后,回路的大信号阶跃响应仿真结果如图5所示。

图5 基于滤波器的Anti-Windup阶跃响应
从仿真结果中可以看出,采用基于滤波器的Anti-W indup补偿后,回路的大信号阶跃响应超调为零,调节时间减小,基于滤波器的 Anti-W indup设计的回路性能优于基于饱和控制的Anti-W indup设计。
3 控制器实现及回路测试
线性控制律以及 Anti-W indup控制律可以通过数字控制器方便地实现,数字控制器分为硬件电路设计和软件算法设计。
3.1 硬件电路
控制器硬件电路结构如图6所示。

图6 控制器硬件电路结构
硬件电路主要由DSP电路、FPGA电路、AD采样电路、CAN通信电路,功放驱动电路组成。DSP电路实现控制算法;FPGA电路完成DSP与外围电路的逻辑接口;AD电路完成电位器、测速机信号的采集;CAN通信电路实现与信号处理机间指令和数据的传输;功放驱动电路采用PWM方式实现电机驱动。
3.2 软件算法
线性控制律以及 Anti-W indup控制律是在连续域内设计完成的,采用数字控制器实现需要进行离散化设计。根据系统带宽和控制实时性要求确定采样频率为1 000 Hz,按采样周期采用双线性变换将连续域设计的控制律转化为离散域的控制算法,最终通过DSP的定时中断完成回路的控制运算。
3.3 回路测试
按上述设计结果,分别采用线性控制律、线性控制律结合饱和控制Anti-W indup、线性控制律结合滤波器Anti-W indup对雷达导引头伺服系统预定回路进行控制,输入50°预定信号,回路测试结果如图7所示。

图7 回路测试结果
从测试结果可知,回路小角度位置预定时,回路主要工作在线性区,线性控制律起主要作用,各种控制方法控制效果相近,回路指标满足系统要求;回路大角度位置预定时,驱动电压饱和非线性对回路产生影响,单独使用线性控制律回路超调增大,不满足系统要求,加入Anti-W indup控制律后超调降低,满足系统要求,基于滤波器的A nti-W indup控制律补偿效果优于基于饱和控制Anti-W indup控制律。
4 结论
对于雷达导引头伺服系统预定回路驱动电压饱和非线性引起的W indup问题,基于饱和控制的Anti-W indup设计和基于滤波器的A nti-W indup设计能有效补偿饱和非线性影响,基于滤波器的A nti-W indup设计的补偿效果更优。采用数字控制器设计能方便地实现两种A nti-W indup控制律,实验测试表明有效验证了不同算法的性能。
[1] 穆虹.防空导弹雷达导引头设计[M].北京:宇航出版社.1996.
[2] 杨明,徐殿国,贵献国.控制系统 Anti-Windup设计综述[J].电机与控制学报,2006,10(6):622-626.
[3] 吴晔,陈峻山.机电驱动机构的线性特性[J].上海航天,2008(3):27-31.
[4] 胡寿松.自动控制原理[M].北京:科学出版社.2002.
[5] Lin Z,Saberi A.Semiglobal Exponential Stabilization of Linear Systems Subject to Input Saturation via Linear Feed baeks[J].Systems&Control Letters,1993,21(3):225-239.
[6] Zheng A,Kothare M V,Morari M.Anti-w indup Design for Internal Model Control[J].Int JControl,1994,60(5):1015-1024.
[7] 董锡君,姚郁,孙彦军.一类 Anti-W indup系统的稳定性研究[J].哈尔滨工业大学学报,1999,31(4):129-132.
[8] 董锡君,姚郁,王子才.基于滤波器的Anti-windup设计及其在伺服系统中的应用[J].哈尔滨工业大学学报,2002,34(1):101-104.
