有机和生物晶体固态核磁共振参数的准确预测

何 睿 焦艳华 梁媛媛 陈灿玉

(杭州师范大学生物医药与健康研究中心,杭州311121)

有机和生物晶体固态核磁共振参数的准确预测

何 睿*焦艳华 梁媛媛 陈灿玉

(杭州师范大学生物医药与健康研究中心,杭州311121)

理论计算有助于复杂的有机和生物系统光谱的鉴定.对于核磁共振光谱,固体结晶中的化学位移和四极耦合常数(QCC)受到邻近的分子和晶格的氢键和范德华作用较大的影响,从而显示出与气态单体分子不同的NMR参数.因此,在固体晶体NMR参数的理论计算中有必要将氢键和范德华作用这两个因素考虑进来.基于周期性方法,本文采用L-Ala-Gly二肽和硝基苯晶体作为模型体系来考察该方法计算NMR参数的精度.研究结果显示周期结构模型能够将分子间的氢键和范德华作用考虑进来,得到的化学位移和QCC值明显优于传统的单分子模型和超分子模型得到的结果,采用该方法计算的结果能够重现NMR实验结果.

核磁共振;四极耦合常数;密度泛函理论计算;氢键作用

1 Introduction

It is well known that carbon,nitrogen,and oxygen are the most common and important elements in organic and biological molecules.The13C and15N NMR experiments are powerful tools for chemical analysis and structure determination of these molecules.114N and17O quadrupole coupling constants(QCCs) are sensitive to the electric charge distribution in solid materials,which can be used to probe the inhomogeneous electric field at the position of the nucleus.Meanwhile,determination of the molecular conformation and dynamic and electrostatic environment of the nuclei by using these NMR parameters is a challenge in both experiment and theory.Although high-speed magic angle spinning nuclear magnetic resonance(MAS NMR)technique has been widely used for these NMR parameters measurements,2-5reliable theoretical predictions of such parameters are of importance in providing supports for the spectral assignments.6-10In particular,the theoretical results are also sustainable for the detailed correlations between NMR(CS and QCC)data and molecular structures(bond lengths and bond angles).11

It is well known that the structures and NMR properties of the crystalline are significantly related to the intermolecular interaction(such as van der Waals(vdW)or hydrogen bonding interaction).Therefore,the NMR properties of the solid state crystalline are much different from the isolated molecular in the free state.6,7Taking L-alanylglycine(L-Ala-Gly)crystalline as example,the monomer model approach has the disadvantage for representing the crystal structure of L-Ala-Gly,and the difference between the predicted and observed values for the principal component δ22of carboxyl carbon in C0(Gly)was as large as 43 by the monomer model calculations.12In order to take the hydrogen-bond interaction(short-range interaction)into account,Tafazzoli and Amini12proposed a new supramolecular model and hydrogen bonding interaction was taken into account with such model.The difference of δ22decreased to 6 when hydrogen bonding interaction was included with the supramolecular model.However,the errors for δ11were still at the level of ca 20 for C0(Ala)and C0(Gly)residues.12It is indicative that the supramolecular model approximation used here has taken account of partial short-range interactions,and ignored the long-range interactions(such as vdW interaction). Therefore,supramolecular model was not large enough to represent the real structure of the crystalline L-Ala-Gly.

In order to include all the short-and long-range interactions during theoretical calculations,we used the developed periodic model to predict the chemical shift and QCC of the solid crystalline.Herein,L-Ala-Gly and nitrobenzene were selected as model crystals,and the short-range effects of the hydrogen bonding and long-range vdW interactions on the shielding tensors(13C and15N)and quadrupole coupling constants(14N and17O)of the organic and biological crystalline were discussed using the periodic model.The calculated NMR parameters in periodic model were compared with the results predicted by the simplified monomer model,supramolecule model,and available experimental results as well.

2 Calculated method

Structural parameters,such as the unit cell size and atomic position of L-Ala-Gly and nitrobenzene crystallines(Fig.1), were deduced from X-ray diffraction(XRD)data.13,14Since the original experimental crystallography data did not report atomic coordinates of the hydrogen nuclei of the methyl group of L-alanine residue in L-Ala-Gly,it is inevitable to optimize the positions of hydrogen atoms for the CH3group by the theoretical methods.Such geometric optimization was accomplished by fixing the volume and the positions of all the other atoms in the unit cell while allowing the three H atoms in the CH3group to relax freely(hereafter denoted as Method 3, and as shown in Fig.2b).It is well known that X-ray diffraction is deficient to determinate the accurate hydrogen atom positions in the crystalline structure.15Then all the other hydrogen atoms of L-Ala-Gly were further optimized(as shown in

Fig.2c and Table 1,and denoted as Method 4).While for nitrobenzene crystalline,we also calculated the NMR parameters on the structure model deduced from crystallographic(XRD) data both before and after structure optimizations.

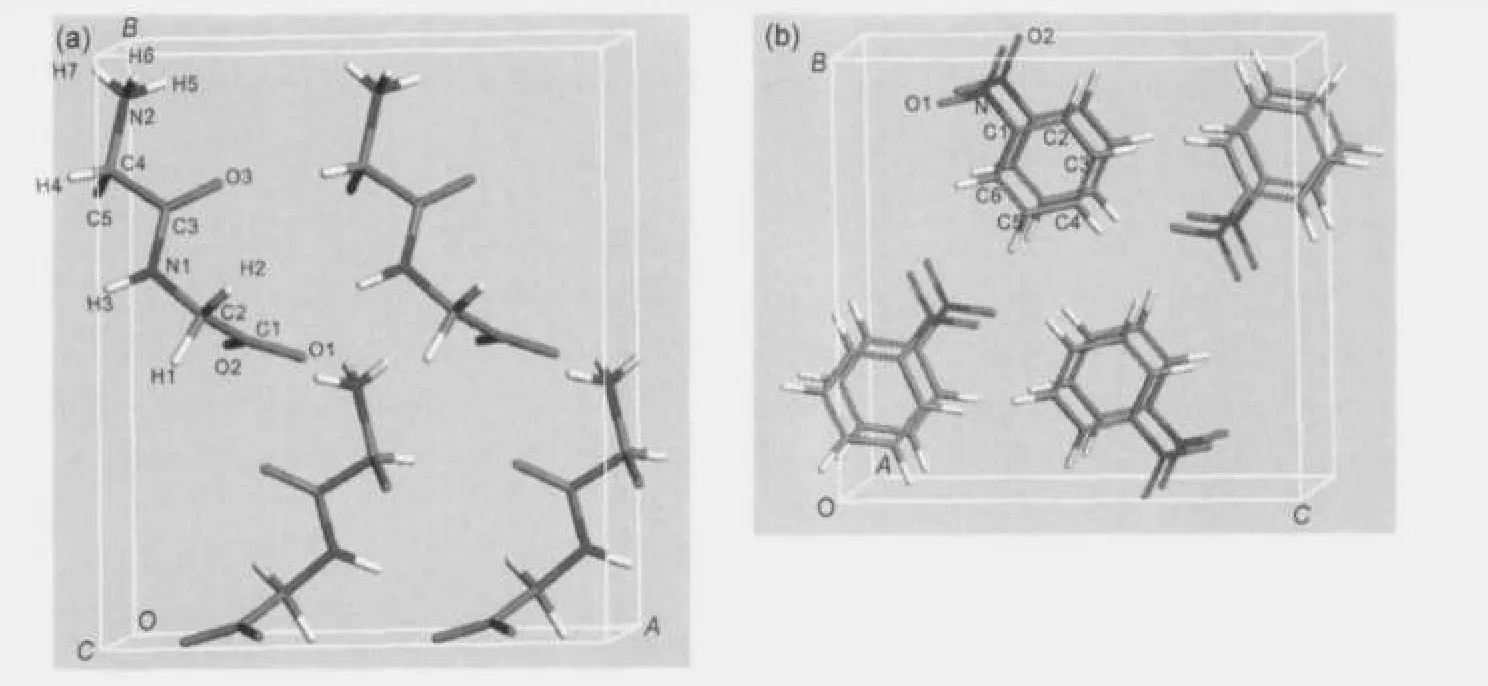
Fig.1 Illustrations of(a)L-Ala-Gly and(b)nitrobenzene periodic structure models used for NMR parameters calculations

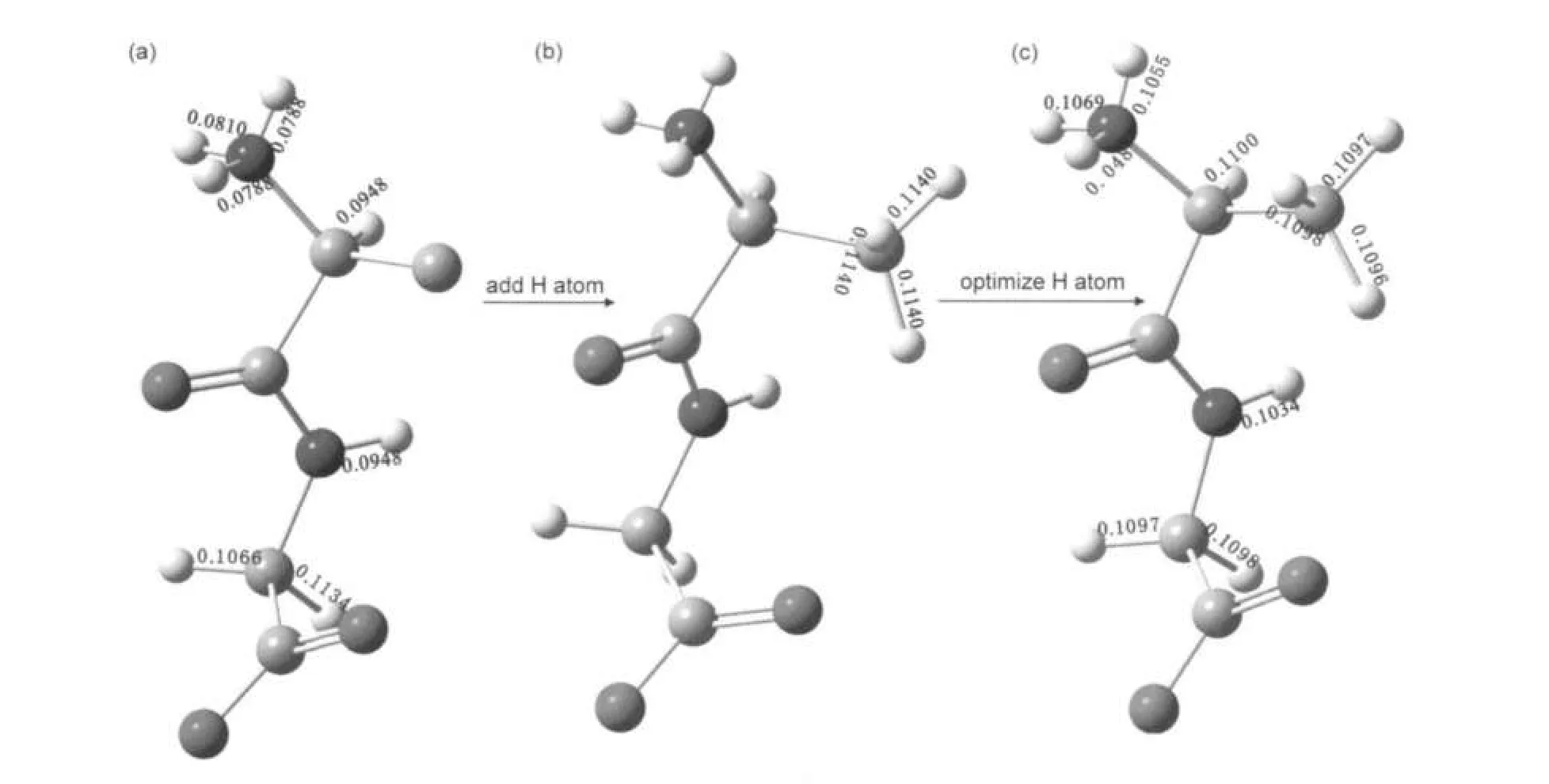
Fig.2 Structure of L-Ala-Gly(a)XRD data did not report atomic coordinates of the hydrogen nuclei of the methyl group of L-alanine residue;(b)after addition of the hydrogen nuclei of the methyl group,only the positions of the CH3were optimized;(c)all the positions of the hydrogen atoms were optimized.Bond lengths(in nm)obtained from both XRD and optimized structures are depicted,indicating a notable elongation in C H and N H bond lengths after structural relaxation.

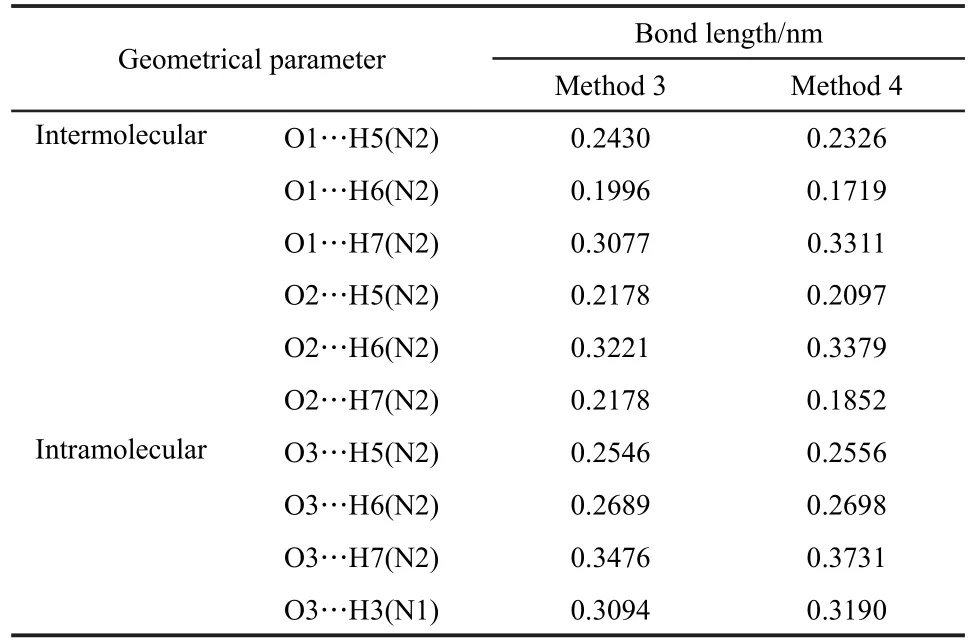
Table 1 Summary of intramolecular and intermolecular hydrogen bonding between O and(N)H atoms in L-Ala-Gly crystalline obtained from different periodic structure models

The atom positions in crystalline solids can normally be determinated by XRD,however,this may not apply to hydrogen atom due to its small scattering cross section for X-ray.We used a partial optimization with the hydrogen atoms relaxed while the rest atoms(C,N,and O atoms)were fixed at their crystallographic locations,which can avoid losing the unique structure of samples due to full optimization.15During the structure optimization and subsequent calculations of NMR parameters,the electron correlation effects were modeled using the generalized gradientapproximation (GGA)proposed by Perdew,Burke,and Ernzerhof(PBE method).16For structure optimizations,the ultrasoft pseudopotentials were used.In addition,a plane-wave cut-off energy of 300 eV and a default medium level Monkhorst-PackK point grid at 2×1×2 and 3×1×1 were adopted to sample the Brillouin zone.17All NMR parameters calculations were performed by the periodic structure method18using a 5×5×5 Monkhorst-PackKpoint grid and by expanding all wavefunctions in a plane-wave basis set by PWscf package.19In order to predict the NMR parameters more accurately,on-the-fly pseudopotential was used.The cut-off energies were set to 800 and 600 eV for L-Ala-Gly and nitrobenzene systems using the NMR predictions.The calculated13C and15N shielding tensors were further converted to chemical shift values,which were referred to the absolute shielding(σ)of liquid TMS(tetramethyl silane)and CH3NO2at room temperature (δsample=σreference-σsample).20The calculated NMR parameters based on the periodic structure models were performed and compared with the available results predicted based on conventional monomer molecular model,supramolecular model,and experimental values obtained from experimental NMR studies.In order to express more easily,we denoted the monomer model,supramolecular model,and periodic structure model whose structure deduced from experimental crystallographic data before and after structural optimization were as Method 1,Method 2,Method 3,and Method 4,respectively.

Owing to the fact that the molecular arrangements in solid powdered samples are spatially anisotropic in nature,the chemical shift will be dependent on the orientations of the molecules in the magnetic field.Thus,by choosing a suitable molecular coordinate system,namely the principle axis system (PAS),the three-dimensional nature of the shielding could be represented by a second-rank tensor,which may be converted to diagonal form with three principle components(δ11,δ22, and δ33).From these components we may define the isotropic chemical shift(δiso)and asymmetry factor(ηδ),assuming that

In principal,the three principle components(δ11,δ22,and δ33) can be measured by various solid-state NMR techniques.Similar to the shielding tensors,the electrical field gradient(EFG) parameters are also presented with three principle components (Vxx,Vyy,and Vzz),and|Vzz|≥|Vyy|≥|Vxx|.The QCC and ηQare defined as:21-23

where e is the electron charge,q is the charge of the electron, Q is the nuclear electric quadrupole moment,and h is the Plank constant.

3 Results and discussion

3.1 Effect of the hydrogen-bonding on the NMR parameters

Due to the complicated hydrogen bonding networks present in peptide crystalline,unacceptable calculated errors of shielding tensors for13C and15N were inevitably obtained compared with experimental values.Taken L-Ala-Gly as a model molecule,intramolecular and intermolecular hydrogen bonding between oxygen and(N)H atom in L-Ala-Gly crystalline were listed in Table 1.In order to take the hydrogen bonding interaction into account,Tafazzoli and Amini12used a five-molecule model to represent the L-Ala-Gly dipeptide crystalline structure.In earlier study,Zheng et al.6,7also performed calculations by combining the supramolecular model with ONIOM method to investigate the effects of the intermolecular hydrogen bonding on the shielding tensors of amino acids.The supramolecular models were constructed by using 12,12,and 10 monomers for α-glycine,L-alanine,and DL-serine,respectively.And Zhan et al.24also used the similar supramolecular model to calculate the13C chemical shift of amino acid samples.The results led us to the conclusion that the13C shielding tensors of carboxyl carbons are readily sensitive to the hydrogen bonding interactions.25

The13C NMR parameters of L-Ala-Gly are listed in Table 2, which includes data obtained from experimental results3and theoretical calculations based on different models,viz.monomer model and supramolecular model proposed by Tafazzoliand Amini,12and the periodic structure models(Methods 3 and 4,this work).Since the single molecule model approach has the disadvantage for representing the crystal structure of L-Ala-Gly,calculated results based on the monomer model failed to reproduce the experimental13C isotropic chemical shift and shielding tensor parameters for all the carbon atoms, and an average error(ca 20)was obtained.The errors for the carboxyl groups would be much larger than the other carbon sites due to the stronger hydrogen bonding interactions between the C＝O groups and H atoms.For example,Comparing the experimental result(182.3)3for the principal component δ22of carboxyl carbon in C0(Gly),the theoretical value by the monomer model was 138.7,the difference between the predicted and observed values was as large as about 43 by the single molecule model calculations.The difference of δ22decreased to about 6 when partial hydrogen bonding was taken into account with the supramolecular model.However,the errors for δ11were still at the level of ca 20 for C0(Ala)and C0(Gly)residues.12It is indicative that the supramolecular model used here has only included the partial local hydrogen bonding interactions and ignored long-range interactions,therefore,such model was not large enough to represent the real structure of the crystalline L-Ala-Gly.

All of the hydrogen-bonding nets of L-Ala-Gly crystalline have been completely included in the periodic models.Therefore,accurate predictions of the NMR parameters at different carbon sites can be obtained(see Table 2).Unlike conventional cluster model calculations,the periodic model adopts a plane-wave basis set with approximated pseudopotentials during calculations.Accordingly,all charge densities and wave functions could be described by the plane-wave basis set,thus facilitating a full representation of crystalline solids and allowing for accurate DFT calculations of both chemical shifts and related NMR parameters in solids.As depicted in Table 2,it is obvious that the values predicted by the periodic model based on the no-optimized crystallographic data are more close to the experimental values,when compared with the results based on Method 1 and Method 2.By comparing with the experimental results observed for all carbons,it may be deduced that the RMSD of the calculated values decreases substantially from 21.2 obtained based on the simplified monomer model and 18.5 for the supramolecular model,to 4.7 for the periodic structure(Method 3)model.Therefore,it suggests that the calculation based on the periodic model is superior to the monomer model(Method 1)and supramolecular model(Method 2).For instance,the δisovalues predicted by the Method 1 for C0(Ala) and C0(Gly)of L-Ala-Gly were 148.1 and 157.7.The Method 2 calculation resulted in slightly better results,which were 155.8 and 163.7,whereas those by Method 3 were 165.0 and 176.8, respectively,indicating a notable improvement compared to the respective experimental13C chemical shifts(171.1 and 179.7)3when the hydrogen bonding interactions were taken into account in the NMR predictions.Similar conclusions can be drawn for other carbon atoms,as listed in Table 2.The maximum error is within 8(Cα(Ala))for the13C isotropic chemical shift for periodic structure model,which was considerably decreased relative to the monomer and supramolecular models. However,24.6(δ33of the Cα(Ala))error is still present for the shielding tensor values,and such derivations maybe arise from the inaccurate hydrogen atom positions.Thus,it may be concluded that by incorporating the hydrogen bonding interactions,notable improvements in predicting the13C shielding tensors may be attained.

Table 2 Theoretical and experimental13C and15N shielding tensors at different C sites for L-Ala-Gly

It is well known that X-ray diffraction method is deficient to locate the accurate hydrogen atom positions in the crystalline structure.15Then it is anticipated that further optimization of the molecular structure model(i.e.,via Method 4)should lead to even more reliable predictions than those predicted by Method 3,as compared to experimental results.Previous theoretical studies have demonstrated that optimized structures could significantly improve the calculated13C and15N shielding tensors of peptides.26,27The optimization of hydrogen atoms should provoke more realistic predictions of atomic positions in the unit cell.Thus,more accurate description of hydrogen bonding interactions,and hence more reliable predictions of NMR parameters will be obtained.As shown in Table 1,the structure optimizations at GGA/PBE level have leaded to the slight increases(typically ca 0-0.003 nm)in N H bond lengths when compared to the crystallographic data.

It is noteworthy that the variation in the positions of the crystalline eventually results in a considerable change(0.01-0.04 nm,as shown in Table 1)in the lengths of the various intermolecular hydrogen bonds,which may probably affect the calculation of NMR shielding tensors.Based on the optimized structures,we recalculated the shielding tensors for L-Ala-Gly and the corresponding data were list in Table 2 as well.In this case, the maximum calculation errors of shielding tensors decrease to 11 for carboxyl group,and the RMSD decreases to 0.83.Obviously,the optimized structure,especially the optimized lengths of intermolecular hydrogen bonds,significantly improves the calculation accuracy of the13C shielding tensors.

Linear fittings of the aforementioned results clearly show that our results calculated based on periodic structure models exhibit superior predictions compared to the conventional monomer model,and such correlation has been illustrated in Fig.3.The quality of the fittings between the calculated(δcal) and experimental(δexpt)shielding tensors are summarized as below:

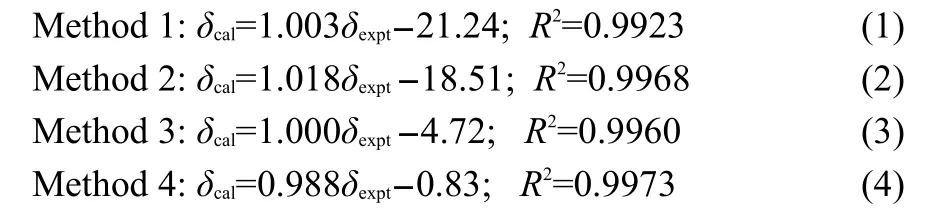
As shown in Fig.3,although the linear fitting of the corresponding dataindicates that all models give rise to a well correlation with the slopes much closer to 1,the intercept of the periodic models(Methods 3 and 4)were considerable closer to zero compared to the single molecule and the supramolecular model models.When comparing the results based on Methods 3 and 4,the later model was much better(the intercept was only 0.83).

Fig.3 Correlations of experimental and calculated13C shielding tensors(δ11,δ22,and δ33)of carbons for L-Ala-Gly obtained from different modelsThe solid line across the diagonal axis represents a perfect match between the experimental and calculated values.Experimental results taken from Ref.3

It is indicative that we can predict the accurate NMR parameters for L-Ala-Gly crystalline on the optimized crystalline structure.Therefore,we also calculated the15N chemical shift, shielding tensors and QCC parameters of the17O and14N atom in L-Ala-Gly crystalline.All these data will be used for the confirmation of the experimental NMR assignments.These data are listed in the Table 2 and Table 3.Compared with the15N shielding tensors by Methods 3 and 4,we can find that the15N shielding tensors are sensitive to the structure parameters,and the optimizations of the hydrogen atom positions have significant effect on the15N shielding tensors.As shown in Fig.1,the N2 atom is bonded with three H atoms to form the NH3group,and all the H atoms are participated in hydrogen bonding interactions with the neighboring molecules.Therefore,the hydrogen bonding interactions presented for the N2 site are stronger than that for the N1 site(present as NH group), which results in a relatively large extend changes in the15N shielding tensors for the N2 sites before and after structure optimization(ca 62 for the δ33).

At the same time,we also predicted the14N and17O QCC constants of L-Ala-Gly by using the periodic models,which are listed in Table 3.It indicates that the hydrogen bonding interactions also have a strong effect on QCC values of the N2 site relative to N1 and all the O sites.Although no experimental results for15N shielding tensors and14N QCC of L-Ala-Gly were reported,the calculated values can be compared with the experimental results of other similar amino acids.In amino acid L-Alanine,15N chemical shift of the NH3sites is-337.1,28which is much close to our theoretical result(-339.1)by the Method 4 for the N2 sites in L-Ala-Gly crystalline(see Tables 2 and 3).The experimental14N QCC values of NH3are 1.18 and 1.21 MHz for α-Glycine29and L-Alanine,30respectively, which are also in good agreement with our calculated result(1.19 MHz).

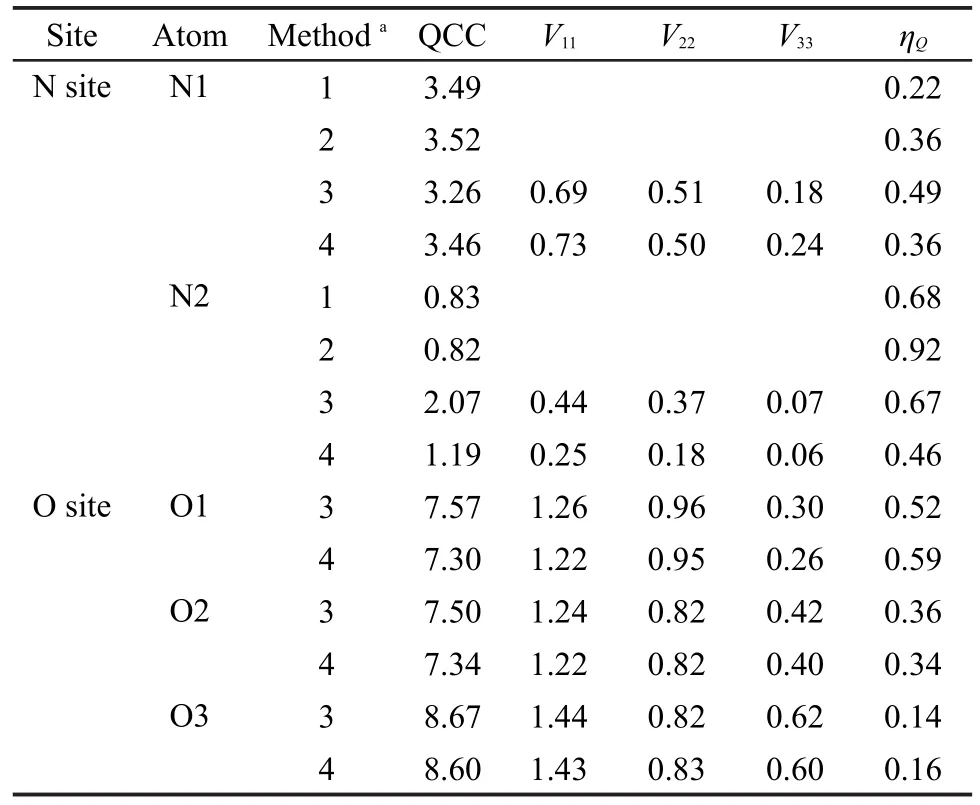
Table 3 Theoretical and experimental14N and17O QCC (in MHz)sites for L-Ala-Gly

3.2 Effect of crystal lattice effects on NMR parameters

On the basis of the above discussion,the hydrogen interactions play an important role in the NMR parameters in biological crystalline.Except for the hydrogen bonding interactions, the long-range van der Waals(vdW)interaction from the lattice(crystal lattice effects),may be another important factor and should be taken into account.As shown in Fig.1b,nitrobenzene is a typical molecular crystal forming by the π-π stacking interactions of the benzene rings,whereas no intermolecular hydrogen bonding interactions exist in the nitrobenzene crystalline.Therefore,it will offer a valuable opportunity to understand the crystal lattice effects on the NMR parameters in the solid crystalline through comparing the results based on the monomer and periodic model of nitrobenzene.

It may be envisaged that B3LYP and MP2(second-order Møller-Plesset perturbation)methods with adequate basis sets can be used to predict reliable NMR parameters for many gaseous organic molecules.Especially,MP2 method has sufficient treatment of electron correlations,and always gives a better result.31,32As shown in the Table 4,the monomer molecule model calculation both at B3LYP and MP2 levels can provide reliable predictions for15N isotropic chemical shifts,typically within 5 errors compared to the experimental data.33Unfortunately, monomer model calculations clearly failed to reproduce shielding tensors for the N site.The15N shielding tensors has been presented ca+24 and-14 errors for the δ11and δ22at the B3LYP/6-311G**level on the X-ray structure.The structure optimization has not improved the calculated results that the errors were+19 and-14 for the δ11and δ22,respectively(see Table 4).Even the shielding tensors predicted at the MP2 level, which has taken the electron correlation effects into account, have the errors of+25 and-12 for the δ11and δ22on the optimized monomer structure.Since the deviations observed for δ11and δ22were with opposite signs and the deviation observed for δ33is small,the isotropic chemical shift value(δiso=(δ11+δ22+δ33)/ 3))is accidentally in close proximity with the experimental result.33

Since there is no hydrogen bonding interactions in the nitrobenzene crystalline,such large calculated errors in the15N shielding tensors indicate that the vdW effect cannot be neglected in the NMR parameter predictions.Then,we predicted the15N shielding tensors by using periodic model with the periodic models method both on the original XRD structure and optimized structure.Fig.4 shows an optimized structure of nitrobenzene crystalline in the periodic model.After the H,N,and O atoms relaxation to stable positions,the C H,C N,and N＝O bond lengths and bond angles were slightly changed. For example,C H elongated to 0.1087-0.1089 nm from 0.0904-0.1030 nm,C N changed from 0.1465 nm to 0.1460 nm,andN＝O bondlengthselongatedto0.1261and 0.1261nm from 0.1223 and 0.1229 nm,respectively.It is noteworthy that the variation of the bond lengths(0.003-0.018nm)results in a considerable change of15N shielding tensors. Based on the periodic model of nitrobenzene crystalline before and after structure optimization,we calculated the shielding tensors and chemical shift for15N,and the corresponding data were listed in Table 4 as well.In this case,calculation errors of shielding tensors decrease to 5 for all three principle components(δ11,δ22,and δ33).Obviously,the periodic model with the structure optimization significantly improves the calculation accuracy of the15N shielding tensors.Furthermore,the13C shielding tensors were also calculated for the different carbon sites of the nitrobenzene crystalline based on the before and after optimization periodic structures.All these data were listed in Table 5,which would usefully render confirmation of NMR spectral assignments.

Table 4 Calculated15N NMR chemical shift parameters for nitrobenzene by different models and methods

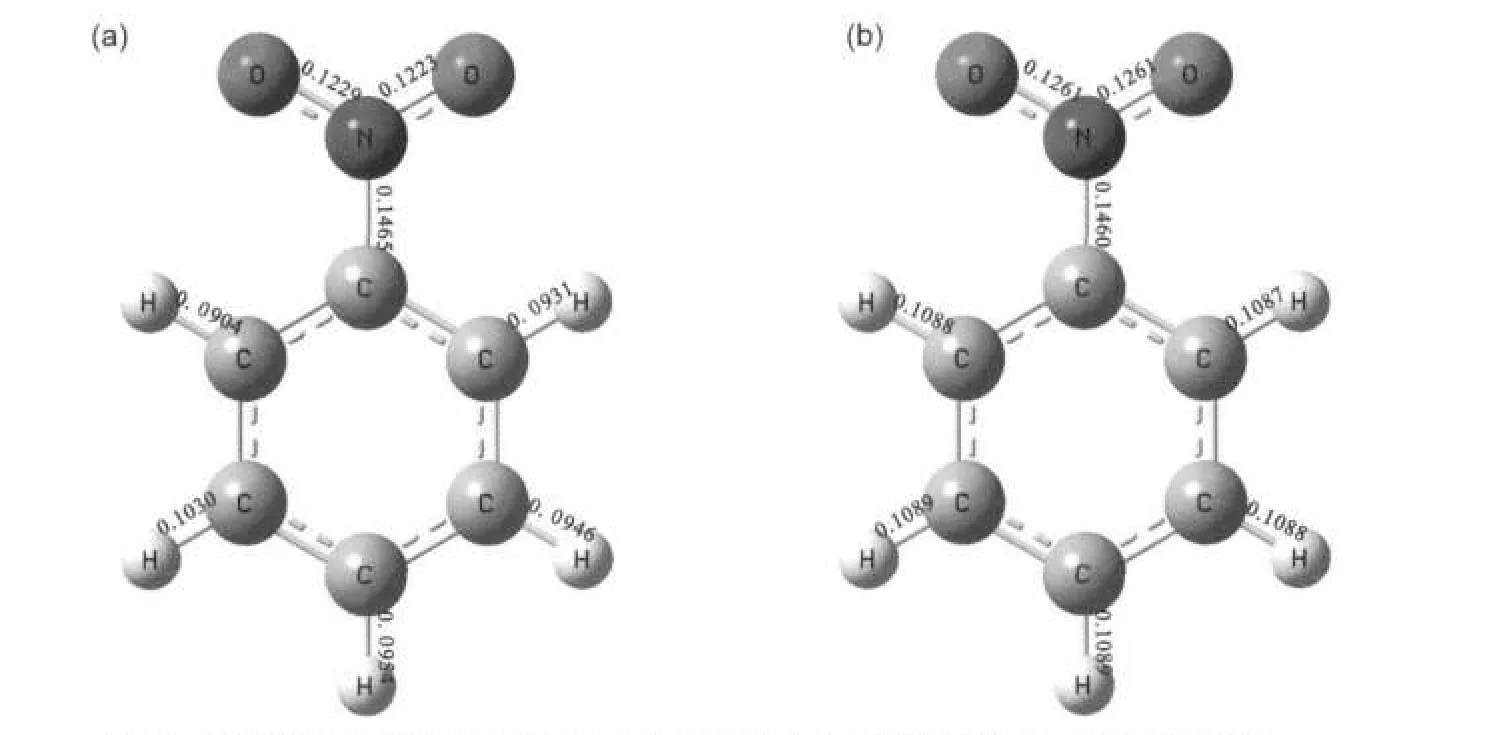
Fig.4 Structures of the nitrobenzene before(a)and after(b)structural relaxation Bond lengths(in nm)obtained from both XRD and optimized structures are depicted,indicating a notable elongation in C H and N=O bond lengths after structural relaxation.For the clarity,only the one molecule in the periodic model of the nitrobenzene crystaline is present.

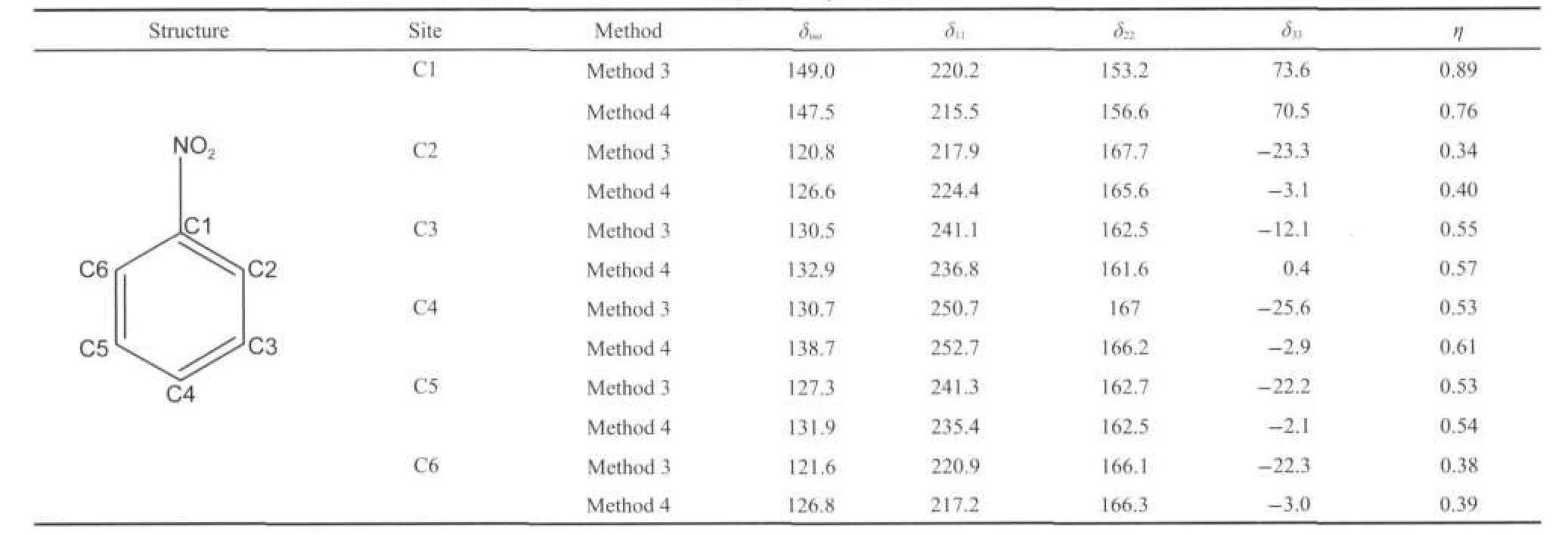
Table 5 Calculated13C NMR shielding tensor parameters for nitrobenzene crystalline

4 Conclusions

We have demonstrated that hydrogen bonding and crystal lattice effects(such as vdW interactions)have considerable effect on the NMR parameters(shielding tensor and QCC)for the organic and biological crystallines.In order to accurately predict the shielding tensors and QCC parameters of the crystalline,it should take two factors into consideration during theoretical calculations.The periodic structural models provide more accurate presentation for short-range hydrogen bonding interactions and the long-range vdW interactions.Therefore,this model dramatically enhanced the calculated accuracy of NMR shielding tensors and QCC parameters for the crystalline.Accordingly, excellent agreements on the13C,15N,and17O shielding tensors parameters at different carbon sites compared to the existing experimental results were achieved for L-Ala-Gly and nitrobenzene crystalline.

From the methodological point of view,the NMR calculations on the periodic model of the crystalline adopted herein is a suitable and efficient approach for the shielding tensors and QCC calculations.Furthermore,the position optimization of hydrogen atoms is much necessary to obtain more accurate results close to the experimental values.

(1) Laws,D.D.;Bitter,H.M.L.;Jerschow,A.Angew.Chem.Int. Edit.2002,41,3096.

(2) Hologne,M.;Faelber,K.;Diehl,A.;Reif,B.J.Am.Chem.Soc. 2005,127,11208.

(3)Wei,Y.;Lee,D.;Ramamoorthy,A.J.Am.Chem.Soc.2001, 123,6118.

(4) Bi,Y.C.;Wang,Y.J.;Wang,J.F.Chin.J.Magn.Reson.2011, 28,177.[毕允晨,王玉娟,王俊峰.波谱学杂志,2011,28, 177.]

(5) Chae,S.;Lee,Y.;Han,O.;Lee,S.Chin.J.Magn.Reson.2010, 27,436.[Chae,S.;Lee,Y.;Han,O.;Lee,S.波谱学杂志, 2010,27,436.]

(6)Zheng,A.M.;Yang,M.H.;Yue,Y.;Ye,C.H.;Deng,F.Chem. Phys.Lett.2004,399,172.

(7) Zheng,A.;Chen,L.;Yang,J.;Yue,Y.;Ye,C.;Lu,X.;Deng,F. Chem.Commun.2005,2474.

(8) Esrafili,M.D.;Behzadi,H.;Beheshtian,J.;Hadipour,N.L. J.Mol.Graph.Model.2008,27,326.

(9) Zheng,A.;Liu,S.;Deng,F.J.Phys.Chem.C 2009,113,15018.

(10) Xu,L.;Li,B.H.;Sun,P.C.Chin.J.Magn.Reson.2010,27, 597.[徐 璐,李宝会,孙平川.波谱学杂志,2010,27,597.]

(11) Moon,S.;Case,D.A.J.Comput.Chem.2006,27,825.

(12)Tafazzoli,M.;Amini,S.K.Magn.Reson.Chem.2008,46,370.

(13) Koch,M.;Germain,G.Acta Crystallogr.B 1970,26,410.

(14)Boese,R.;Blaser,D.;Nussbaumer,M.;Krygowski,T.M. Struct.Chem.1992,3,363.

(15) Squires,G.L.Introduction to the Theory of Thermal Neutron Scattering,2nd ed.;Dover Publications Inc.:New York,1996.

(16) Perdew,J.P.;Burke,K.;Ernzerhof,M.Phys.Rev.Lett.1996, 77,3865.

(17) Monkhorst,H.;Pack,J.D.Phys.Rev.B 1976,13,5188.

(18) Bryce,D.;Bultz,E.Chem.Eur.J.2007,13,4786.

(19) Giannozzi,P.;Baroni,S.;Bonini,N.;Calandra,M.;Car,R.; Cavazzoni,C.;Ceresoli,D.;Chiarotti,G.L.;Cococcioni,M.; Dabo,I.;Dal Corso,A.;Fabris,S.;Fratesi,G.;de Gironcoli, S.;Gebauer,R.;Gerstmann,U.;Gougoussis,C.;Kokalj,A.; Lazzeri,M.;Martin-Samos,L.;Marzari,N.;Mauri,F.; Mazzarello,R.;Paolini,S.;Pasquarello,A.;Paulatto,L.; Sbraccia,C.;Scandolo,S.;Sclauzero,G.;Seitsonen,A.P.; Smogunov,A.;Umari,P.;Wentzcovitch,R.M.J.Phys.: Condes.Matter 2009,21,395502.

(20) Trevino,S.F.;Prince,E.;Hubbard,C.R.J.Chem.Phys.1980, 73,2996.

(21) Freude,D.;Haase,J.Quadrupole Effects in Solid-State Nuclear In Magnetic Resonance.In NMR Basic Principles and Progress; Springer-Verlag:Berlin,1993;Vol.29,pp 1-90.

(22) Vega,A.J.Quadrupolar Nuclei in Solids.In Encyclopedia of Magnetic Resonance;John Wiley&Sons,Ltd:New York, 1996;Vol.6,p 3869.

(23) Man,P.P.Quadrupole Couplings in Nuclear Magnetic Resonance,General.In Encyclopedia of Analytical Chemistry; John Wiley&Sons,Ltd.:New York,2000;p 12224.

(24) Chen,X.;Zhan,C.G.J.Mol.Struct.-Theochem 2004,682,73.

(25)Zheng,A.;Liu,S.B.;Deng,F.J.Comput.Chem.2009,30,222.

(26)Birn,J.;Poon,A.;Mao,Y.;Ramamoorthy,A.J.Am.Chem.Soc. 2004,126,8529.

(27) Strohmeier,M.;Grant,D.M.J.Am.Chem.Soc.2004,126,966.

(28) Gervais,C.;Dupree,R.;Pike,K.J.;Bonhomme,C.;Profeta, M.;Pickard,C.J.;Mauri,F.J.Phys.Chem.A 2005,109,6960.

(29) Edmonds,D.T.;Speight,P.A.Phys.Lett.A 1971,34,325.

(30)Naito,A.;Ganapathy,S.;Akasaka,K.;McDowell,C.A. J.Phys.Chem.1981,76,3190.

(31) Moore,E.A.Chem.Phys.Lett.2000,317,360;

(32) Schindler,M.J.Am.Chem.Soc.1987,109,5950.

(33) Penner,G.H.;Bernard,G.M.;Wasylishen,R.E.;Barrett,A.; Curtis,R.D.J.Org.Chem.2003,68,4258.

June 3,2011;Revised:July 8,2011;Published on Web:July 26,2011.

Accurate Predictions of the NMR Parameters in Organic and Biological Crystallines

HE Rui*JIAO Yan-Hua LIANG Yuan-Yuan CHEN Can-Yu
(Research Center of Biomedicine and Health,Hangzhou Normal University,Hangzhou 311121,P.R.China)

Theoretical predictions are helpful for the spectroscopic identification of complicated organic and biological systems.For nuclear magnetic resonance(NMR)parameters,however,the chemical shift and quadrupole coupling constant(QCC)of the solid crystals are considerably affected by hydrogen bonding and van der Waals interactions from neighboring molecules and the crystal lattice leading to significant spectroscopic differences compared to isolated monomer molecules.Therefore,it is necessary to take these two factors into account for the precise predictions of chemical shifts and QCCs of solid crystals.L-alanylglycine dipeptide and nitrobenzene were selected as model crystals to demonstrate these effects.Here,the chemical shielding(CS)and QCC data were calculated based on the periodic structure model.The incorporation of intermolecular hydrogen bonding and crystal lattice effects by periodic models was found to be crucial in obtaining reliable predictions of CS and QCC values and rendering more explicit spectroscopic assignments for solid organic and biological systems.

NMR;Quadruple coupling constant;DFT calculation;Hydrogen bonding interaction

O641

∗Corresponding author.Email:herui@hznu.edu.cn;Tel:+86-571-28862722.

The project was supported by the Science and Technology Development Program of Hangzhou,China(20091133B09),Zhejiang Provincial Medicine&Health Research Fund,China(2009A158),and Zhejiang Provincial Public WelfareApplication Project of China(2010C33132).

杭州市科技发展计划项目(20091133B09),浙江省医药卫生科研基金(2009A158)和浙江省公益性技术应用研究计划项目(2010C33132)