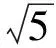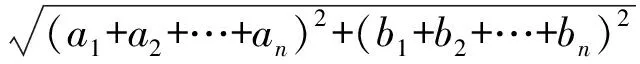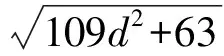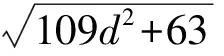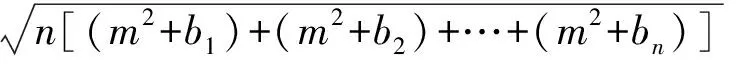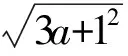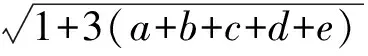一道竞赛试题的推广与引申
2011-11-27
●
(春谷中学 安徽南陵 241300)
一道竞赛试题的推广与引申
●邹守文
(春谷中学 安徽南陵 241300)
由《中学数学教学参考》组织的第4届中学生数学智能通讯赛八年级有这样一道试题:
设0 这是一道笔者提供的题目,通过对该题的分析,获得下面的推广与引申. 命题1设正实数a,b,x,y满足a 先证明下面的引理. 引理设P为△ABC内一点,则 AB+AC>PB+PC. 证明如图1,延长BP至点D,则 AB+AD>BD,PD+DC>PC, 相加得 AB+AC+PD+>BD+PC, 即 AB+AC>PB+PC. 图1 图2 下面对命题1进行证明. 证明构造如图2所示的矩形ABCD,使AN=a,CM=b,PN=x,PM=y,则 在△APC中,AP+PC≥AC,因此 又由引理知,在△ANC中,有 AP+PC 从而 故 说明这里采用了构造法,非常直观. 在命题1中,令a=b=1,y=1-x,即得第4届中学生数学智能通讯赛试题. 只需在命题1中取x=1,y=2,a+b=2,即得 累次运用命题1左边的不等式,可以得到更一般性的形式: 命题2设a1,a2,…,an;b1,b2,…,bn为正实数,则 运用命题2能够非常简单地解决一类代数最小值问题. 解当x>12时,y没有最大值和最小值;当x<0时,y也没有最大值和最小值. 当0 因为 所以y的最小值为13. 累次运用命题1右边得不等式,又可以得到: 命题3设a1,a2,…,an;b1,b2,…,bn为正实数,且a1 特殊情况:当a1=a2=…=an时,有 推论1设b1,b2,…,bn,m为正实数,则 例2已知a,b,c,d,e是正实数,且a+b+c+d+e=2,求证: 证明由推论1知 对命题2和命题3进行引申,又能得到: 命题4设m为正实数,b1,b2,…,bn为非负实数,则 证明首先证明:设m为正实数,b1,b2为非负实数,则 ⟺ ⟺ ⟺ (m2+b1)(m2+b2)≥m2(m2+b1+b2) ⟺ b1b2≥0, 且b1,b2为非负实数,所以最后一式显然成立.累次运用上述不等式,得 考虑命题4的上界,有 命题5设m为正实数,b1,b2,…,bn为非负实数,则 证明由方差公式知 所以 故 于是 命题4和命题5在求一类非负数的取值范围或不等式的证明时往往能起到一定的作用. 例3已知正实数a,b,c,d,e满足a+b+c+d+e=1,求证: 证明由命题4,可得 [1] 王怀祥,白平.例说构造矩形或正方形求最小值[J].初中数学教与学,2011(1):26-27. [2] 干超一.轮换对称式最值求法[J].中等数学,2011(2):15-18.