一种凹多边形凸分解的全局剖分算法
2011-11-27贺怀清
贺怀清,杨 鹏
(中国民航大学计算机科学与技术学院,天津 300300)
在现有的较为成熟的扫描算法当中,轮廓偏置扫描算法[1]由于不需要频繁开关激光器,且扫描中不断改变方向,能够获得较好的精度。但是由于在偏置的过程中,要不断地检查环自交、环相交等情况,因此算法效率不高。对此,不少学者提出结合计算几何当中的凹多边形凸分解算法[2-5]将多边形[6]分解为多个凸多边形,再分别对每个凸多边形进行轮廓偏置的算法。
文献[2]中通过对凹点进行分类及编码,有效地减少了简单多边形的个数,但是编码较为复杂;文献[3]对文献[2]进行了改进,提出了在凹点的可视点对之间通过权函数来进行剖分;文献[4]在Rogers.F.David提出的经典算法之上提出了基于顶点可见性的剖分算法,根据当前凹点的权函数来进行剖分,结果不够全面;文献[5]提出了一种较为简化的可视点串求取算法,并在改进了的权函数基础之上进行剖分,效果较好。
本文首先对局部剖分算法的原理及存在的问题进行了阐述,并对基于正负法搜索可视点串的算法进行了更正和改进,然后利用改进的权函数从全局剖分的角度选择最优的剖分点进行剖分,优化了简单多边形的形态质量。通过在各个子轮廓上进行轮廓偏置扫描,得到了较好的实验结果。
1 基本概念与定义
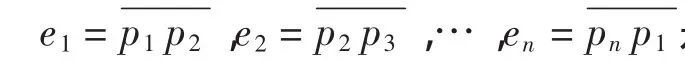
定义2 若多边形P的顶点序列p1,p2,…,pn按照逆时针方向排列,并且点pi+1在pi-1pi的左(右)侧,则称点pi为凸(凹)点[6]。以凸(凹)点为顶点的内角≤π(>π)。
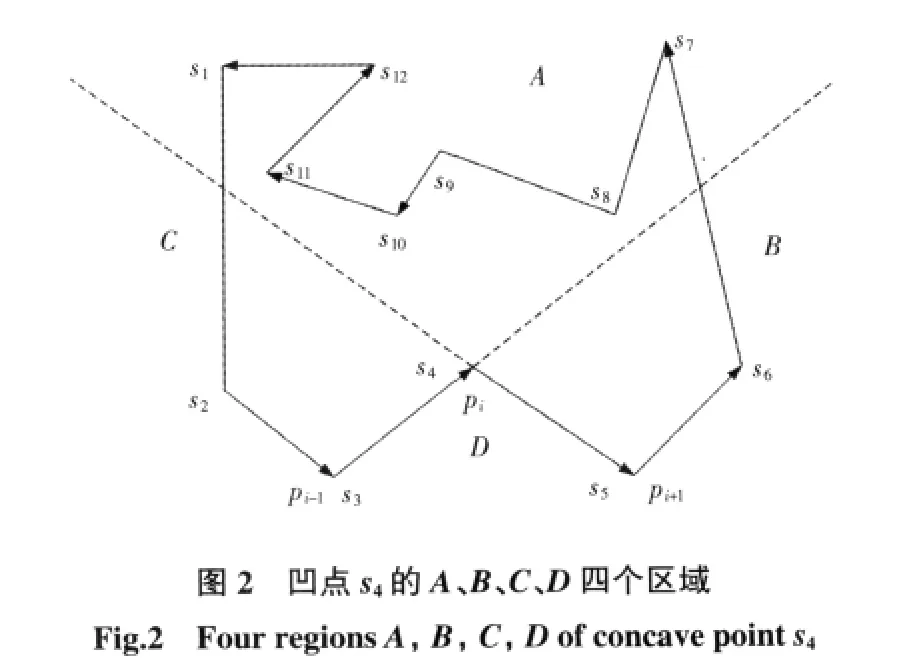
定义3 可视点[7]:对于多边形的任意顶点s来说,多边形中所有顶点与s连线形成的线段,若全部在多边形内部或者边上面,则称s为可视点。如图1所示,顶点 s4的可视点有 s2、s3、s5、s6、s8、s9、s10、s11。因为 s4同顶点s1、s7、s12的连线不完全在多边形轮廓内,所以其不是s4的可视点。

定义4 最佳剖分[2]:如果剖分线连接两个凹点,同时这两个凹点在分属的两个子多边形上表现为凸点,即为最佳剖分。
定义5 正负法[5]:对于任意直线方程F(x,y)=0,它可把平面划分为3个区域,从而形成3个点集:
1)满足F(x,y)=0的点的集合,即直线上各点;2)满足 F(x,y)> 0的点的集合,成为 F+区;3)满足 F(x,y)< 0的点的集合,成为 F-区。直线AB的直线方程函数为F(x,y)=x(YB-YA)+y(XA-XB)+YA·XB-XA·YB(1)其中:AB 的端点坐标为 A(XA,YA)、B(XB,YB)。沿着直线AB的起点A到终点B,F-区总是在AB的左侧,F+区在AB的右侧。
2 局部剖分算法
局部剖分算法是指每次剖分只针对一个凹点,并且只需考虑如何引出剖分线来消除当前凹点的算法。
2.1 算法原理
如图2所示,从多边形的第1个顶点s1开始搜索,搜索到的第1个凹点pi,记录pi沿着轮廓线方向之前和之后相邻的点,并标记为pi-1、pi+1,沿着pi-1pi、pi+1pi方向把轮廓线分成A、B、C、D四个区域。其中:
A:射线pi-1pi和pi+1pi形成的扇形区域(包括射线pi-1pi和pi+1pi);
B:射线pi-1pi、pi+1pi反向射线形成的扇形区域;
C:射线pi+1pi、pi-1pi反向射线形成的扇形区域;
D:pi-1pi的反向射线与pi+1pi的反向射线形成的扇形区域。
从图2中可以明显看到,在pi处要得到最佳剖分,则另一个剖分点必须落在区域A中。用SA、SB和SC分别表示轮廓线在A、B、C区域形成的可视点串。
2.2 存在的问题
采用这种算法效率较高,但其存在如下的缺陷:①一次剖分消去两个凹点形成最佳剖分的概率较小;②无法保证剖分后的多边形形态质量。
3 全局剖分算法
考虑到局部剖分算法的上述缺点,本文在局部剖分算法基础之上提出了一种全局剖分算法。首先对当前轮廓上的所有凹点进行最优剖分点的处理,之后从其中选取当前轮廓的最优剖分点进行剖分。
在对凹点进行最优剖分点的处理时,要进行当前凹点的可视点串的求取以及最优剖分点的选取。
3.1 改进的可视点串求解算法
本文所提出的算法是在文献[5]算法的基础上进行的改进。采用文献[5]中提出的正负法原理来搜索可视点串,更正其在求取B区内最后一点和C区内第一点时可能出现的错误,同时改进如何确定可视点串的算法。
如图2所示,记pi-1pi方向的直线方程为Fi-1(x,y),记pi+1pi方向的直线方程为Fi+1(x,y)。则在A区域的点应满足的条件为Fi-1(x,y)≤0,同时Fi+1(x,y)≥0。由于可视点串是在A区域的点,但是轮廓线上出现在A区域的顶点并不一定都是可视点,因此应首先得到A区域的顶点,之后再筛选出可视点。
3.1.1 凹点A区域顶点串的求取
下面首先通过一遍搜索确定轮廓线P在A区域内的顶点并添加到临时点串tempA中。pi指向当前凹点的顶点指针。从凹点pi的后继结点p沿着逆时针方向开始搜索,直到重新搜索到凹点pi为止。
3.1.2 可视点串的确定
当得到凹点pi位于A区的轮廓线点串之后,根据定义3中可视点的定义,进一步得到凹点pi的可视点串SA。文献[5]中求取可视点串SA时,从tempA顶点方向考虑进行滤除,从tempA的第1点开始依次取出各点作为待定可见点,将其与凹点pi形成待定剖分连线,利用正负法判断该点在tempA顶点串中位置之后的所有点是否都在待定剖分连线的左侧(在直线的左侧是指当前顶点代入直线方程得到的值小于0,在直线的右侧是指当前顶点代入直线方程得到的值大于0),如果其余各点确实在连线左侧,则该点为可见点,如图3所示。
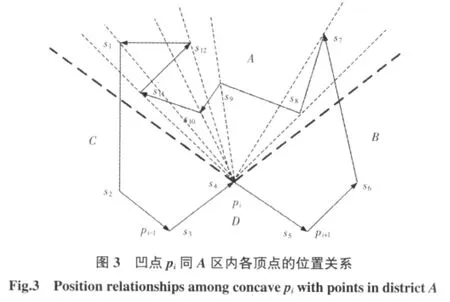
下面分两个步骤对算法进行描述:①判断在顶点串tempA中的位置出现在pot之前的顶点是否都满足Fi(x,y)≥0;②判断出现在pot之后的顶点是否都满足Fi(x,y)≤0,如果同时满足这两个条件,就作为凹点的可视点,添加到凹点的可视点串当中,其中p、q、r是tempA上的顶点指针,p指向第1个顶点。描述如下:
1)q指向p的后继,r指向p,进入循环。判断q是否在凹点pi和p构成的直线的左侧,即F(x,y)是否小于等于0。如果小于等于0,q指向其下一个节点,继续判断q是否在凹点pi和p构成直线的左侧;如果大于0,则判断凹点pi和p在r与q构成直线的同侧或者异侧(直线同侧是指两顶点同时在直线的左侧或者右侧,直线异侧是指两顶点不同时位于直线的同一侧),如果同侧,那么q指向其下一个节点,继续循环,直到q为空,表明在p之后的顶点都满足条件,转2);如果出现在异侧,当前q循环结束,p指向q,继续判断剩余的顶点是否是可视点,转1)。
2)如果对于当前顶点p之后出现的所有顶点都在凹点pi同顶点p构成的直线左边,即q为空时,判断顶点p之前出现的顶点是否都在凹点pi同顶点p构成的直线右边。令r指向tempA的头顶点,q指向r,进入循环。判断r是否在凹点pi和p构成的直线的右侧,即 F(x,y)是否大于等于 0,如果 F(x,y)大于等于0,r指向下一个顶点,q指向r的前驱,继续循环;如果F(x,y)小于0,判断凹点 pi和顶点 p是否在 r和 q构成的直线的同侧,如果在同侧,r指向下一个顶点,继续循环,如果出现在异侧,当前r循环结束,p指向其下一个顶点继续判断步骤1)。如果r循环结束时,r等于p,表示顶点p之前出现的顶点都在凹点pi同顶点p构成的直线右边,则顶点p是可视点,添加到凹点pi的可视点串SA中去,同时p指向下一个顶点,如果p不为空,转1);否则可视点串求取结束,程序退出。
3.2 最优剖分点的选取
对于权函数的选取,主要的算法思想[3,8]是:尽量使得剖分线在凹点的角平分线上,这样可以使得凹点剖分后的两个角大小相差不大,保证剖分后多边形的形态质量。文献[3]给出了比较详细的描述,文献[8]对文献[3]中的权函数进行了改进,本文中选取的权函数是在文献[8]的基础上重新加入文献[3]中的控制参数。下面是根据文献[8]中给出的权函数描述

其中:对于顶点pi的权函数来说,当pi为凹点或凸点时,wi=f(α,β)。当pi为凹点时,α、β如图4(a)所示;当 pi为凸点时,α、β 如图 4(b)所示。
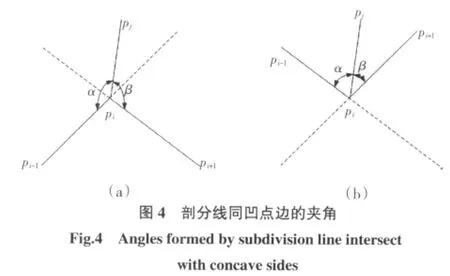
对于顶点pi和pj构成应取得的权值为

其中:m、n即是控制函数,当顶点pi、pj都为凹顶点时,m、n值都相同;当pi为凹顶点,pj为凸顶点时,n取值大于m,能够有助于提高获得的形态质量[3]。
3.3 全局剖分算法描述
算法是递归进行的。算法的输入是凸多边形的轮廓线的指针,由于都是外轮廓线,所以顶点都是按逆时针方向排列的点列。算法具体描述如下:
第1步:遍历简单多边形P,建立凹点串。依次从P中取出顶点,判断其是否是凹点[9],如果是凹点,记录其前驱和后继并置标识为未访问,添加到凹点串中。遍历结束如果程序中无凹点,则当前多边形P为凸多边形,可以直接进行后续的扫描算法,程序退出;否则继续进行分区。
第2步:依次搜索凹点串中未访问凹点,采用改进的可视点串求解算法求出可视点串SA及B区内最后一点和C区内第一点。
第3步:遍历凹点串,利用权函数从每个凹点中找到最优的剖分点、权值和剖分类型并保存下来,剖分类型用一个int类型的变量divideType来记录,剖分点为凹点时值为1,为凸点时值为2,为辅助点时值为3,辅助点即为SB中的最后一个点bEnd与SC中的第一个点cBegin同凹点的角平分线相交得到的交点,divideType初始时值为0。
第4步:遍历凹点串,按照以下次序找出权值最小的凹点:首先是剖分类型变量为1,即最佳剖分;如果没有,再找剖分类型变量为2的凸点剖分;最后是辅助点剖分。也就是尽量使得一次剖分能够消去两个凹点,减少剖分的次数。
第5步:根据凹点和剖分点分解原多边形成两个新的多边形并添加到多边形链表中去,同时从多边形链表中删除原多边形,接着递归地对两个新生成的多边形进行凹多边形的凸分解,直到没有凹点为止。
4 实例结果
在已搭建好的快速成型软件平台上,对图5中左图模型在凸分解的基础之上进行轮廓偏置扫描。通过对切片轮廓进行凹多边形凸分解算法,将原简单多边形划分为了4个凸多边形。从扫描结果图中可以看到,扫描结果良好。

5 结语
本文在对比分析了已有凹多边形凸分解算法的基础之上,对正负法搜索凹点的可视点串的算法进行了深入分析,更正了其不足,并对其进行了改进;添加了对最佳剖分时可能出现多余多边形合并的考虑,同时从全局剖分的角度选取最优剖分点,保证了分解后多边形的形态质量,通过实验结果可以看出,算法运行良好。
[1]YANG Y,LOH H T,WANG Y G,et al.Equidistant path generation for improving scanning efficiency in layered manufacturing[J].Rapid Pro totyping Journal,2002,8(1):30-37.
[2]肖忠晖,卢振荣,张 谦.简单多边形凸单元剖分的编码算法[J].计算机学报,1996,19(6):477-481.
[3]王钲旋,李文辉,庞文阶.一个加权剖分简单多边形为凸多边形的算法[J].计算机学报,1998,21(3):229-233.
[4]金文华,饶上荣,唐卫清,等.基于顶点可见性的凹多边形快速凸分解算法[J].计算机研究与发展,1996,36(12):1455-1460.
[5]卞宏友,刘伟军,赵吉宾,等.面向快速制造扫描分区的凹多边形凸分解算法[J].计算机应用,2005,25(9):2143-2145.
[6]周培德.计算几何—算法设计与分析[M].3版.北京:清华大学出版社,2008:47-48,53.
[7]朱传敏,唐 珺,许田贵.凹多边形凸分解算法在快速原型中的应用[J].现代制造工程,2010(2):53-56.
[8]张玉连.改进的加权剖分简单多边形为凸多边形的算法[J].燕山大学学报,2001,25(1):76-79.
[9]刘润涛.任意多边形顶点凸、凹性判别的简捷算法[J].软件学报,2002,13(7):1309-1312.
