内共振条件下大范围直线运动梁的分岔分析

王 霞，李建平

(河南工程学院 数理科学系，河南 郑州 451191)

近几十年来，大范围直线运动梁由于其在机械工程、建筑、航空航天以及汽车等领域都有着广泛的应用，引起了国内外学者的关注.目前，关于大范围直线运动梁已经有了大量的文献和研究成果，比如Nayfeh和Mook[1]采用多尺度法一次近似展开，分析了文献[1]中悬臂梁的参激共振稳定性问题.Hyun等[2]采用多尺度法二次近似展开，对文献[1]中的梁系统作了更细致的稳定性研究.Kane等[3]较早地建立了非惯性场中悬臂梁的动力学方程，而Chin和Nayfeh[4-5]研究了3∶1内共振梁由参激共振引起的非线性动力学行为问题，对梁的第一、二阶模态主参激共振及一、二阶模态间组合参激共振作用下的非线性梁系统分别做了研究.最近，冯志华和胡海岩[6-8]基于Kane方程，建立了具有三次几何及惯性非线性项的大范围直线运动梁模型，对含内共振现象的大范围直线运动两端铰支梁的参激振动平凡解的稳定性进行了详细的分析与研究.然而，这些文献大多都是利用数值的方法讨论了大范围直线运动梁的稳定性，而利用解析的方法讨论大范围直线运动梁稳定性的文献相对较少.本文主要利用稳定性分析和特征值分析等解析方法研究了3∶1内共振条件下大范围直线运动梁的分岔解及其稳定性情况，并给出了其相应的临界分岔曲线.

1 建立模型

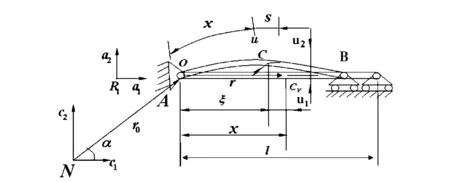
图1 非惯性系中两端铰支梁Fig.1 Configuration of a simply supported beam under a large linear motion of basement

根据文献[6-8]，基于Kane方程，利用Rayleigh-Ritz法，可以得到铰支梁的无量纲控制方程如下：

(1)

引入如下频率调谐因子σ1和σ2，使得ω=2ω2+εσ1，ω2=3ω1+εσ2.利用多尺度法，可得到第二阶模态主参激共振时系统的调制方程组为:

(2)

在(2)中利用变换

x1=r1sin(θ1),x2=r1cos(θ1),x3=r2sin(θ2),x4=r2cos(θ2),

(3)

可得

(4a)

(4b)

(4c)

(4d)

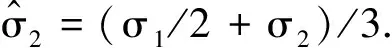
2 分岔分析

2.1 初始平衡解

由方程组(2)可知，系统存在初始平衡解(x1,x2,x3,x4)=(0,0,0,0).初始平衡解的稳定性由系统(2)在初始平衡解处的Jacobi矩阵所决定，其相关的特征方程为

(5)

则初始平衡解的稳定条件为:

(6)

(7)

2.2 单模态解——Hopf分岔解

本节主要讨论由初始平衡解分岔出的单模态解(7)的存在条件和稳定性.重新标注单模态解(7)为如下形式:

(8a)

(8b)

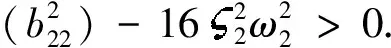
(1)当c22>0时，

(2)当c22<0时，

下面讨论单模态解(8)的稳定性.系统(2)在单模态解(8)处的Jacobi矩阵的特征方程为

(9)

根据Routh-Hurwitz准则，单模态解(8a)将分岔为1模态分岔解，此时分岔点为

(10)

而单模态解(8b)将分岔为另一个1模态分岔解，此时分岔点为

(11)

在分岔点(10)和(11)处r2的值分别为

(12)

(13)

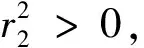
(1)当3c12ω2-ω1c22>0时，

(2)当3c12ω2-ω1c22<0时，

由Routh-Hurwitz准则，根据文献[9]可知，单模态解的稳定条件为

由此不等式可得稳定边界，即临界分岔曲线为

此时，沿着临界分岔曲线L2发生广义静态分岔，单模态解将分岔为拟周期解——2维胎面.

2.3 双模态解——拟周期解

由方程(4)可知，拟周期解(r2≠0，r1≠0)满足如下方程:

(14a)

(14b)

考虑系统(2)在拟周期解处的Jacobi矩阵为:

(15)

其中,bij(i=1，2，3，4),见附录.其相关特征方程为

P(λ)=λ4+a1λ3+a2λ2+a3λ+a4.

(16)

由Routh-Hurwitz判据，拟周期解的稳定条件为：

(17)

由不等式(17)可得2条临界分岔曲线，其中一条临界分岔曲线为

在此临界线上发生静态分岔；另一条临界分岔曲线为

沿此临界线出现Hopf分岔，并有可能产生一个3维胎面.

3 结论

本文利用解析方法研究了一类3∶1内共振条件下大范围直线运动梁的稳定性与分岔行为.对第二阶模态主参激共振条件下的梁系统的稳定性与分岔行为进行了分析.在第二阶模态主参激共振时，利用稳定性分析和特征值分析等解析方法，对平均方程进行了研究，给出了梁系统的静态分岔、Hopf分岔、2维胎面以及3维胎面等分岔解及其存在的条件和稳定性情况，并给出了相应的临界分岔曲线.本文的结果为这类模型的分析与设计提供了依据.

参考文献：

[1] Nayfeh A H, Mook D T. Nonlinear Oscillations[M]. New York: Wiley, 1979.

[2] Hyun S H, Yoo H H. Dynamic modeling and stability analysis of axially oscillating cantilever beams[J]. Journal of Sound and Vibration, 1999, 228(3): 543-558.

[3] Kane T R, Ryan R R, Banerjee A K. Dynamics of a cantilever beam attached to a moving base[J]. Journal of Guidance Control and Dynamics, 1987, 10(2): 139-151.

[4] Chin C M, Nayfeh A H. Three-to-one internal resonances in hinged-clamped beams[J]. Nonlinear Dynamics, 1997, 12(2): 129-154.

[5] Chin C M, Nayfeh A H. Three-to-one internal resonances in parametrically excited hinged-clamped beams[J]. Nonlinear Dynamics, 1999, 20(2): 131-158.

[6] 冯志华，胡海岩. 内共振条件下直线运动梁的动力稳定性[J]. 力学学报，2002, 34(3): 389-399.

[7] Feng Z H, Hu H Y. Principal parametric and three-to-one internal resonances of flexible beams undergoing a large linear motion[J]. Acta Mechanica Sinica, 2003,19(4): 355-364.

[8] Feng Z H, Hu H Y. Largest lyapunov exponent and almost certain stability analysis of slender beams under a large linear motion of basement subject to narrowband parametric excitation[J]. Journal of Sound and Vibration, 2002, 257(4): 733-752 .

[9] Mcdonalda R J, Sri Namachchivaya N. Pipes conveying pulsating fluid near a 0∶1 resonance: local bifurcations[J]. Journal of Fluids and Structures, 2005(21): 629-664.