基于独立成分分析技术的语音除噪系统
2011-11-24袁莉芬
袁莉芬,刘 辉,程 俊
(湖南师范大学物理与信息科学学院,中国 长沙 410081)
在语音通信与处理控制系统中,信号不可避免地会被噪声污染,特别在小信号采集和测量中,噪声干扰显得尤其严重.因此,如何消除实际语音信号中的噪声,从混有噪声的信号中提取有用信息一直是现代语音处理学科研究的焦点之一.
语音除噪的目的在于在强噪声背景环境下尽量不失真的提取语音信号、提高语音信号的信噪比.较常用的语音除噪技术包括LMS/RLS算法[1]、小波处理[2-5]等.这些技术从本质上来说即滤波技术,如维纳滤波[6]、卡尔曼滤波[5,7]以及阀值法去噪等[8].其中维纳滤波要求带噪信号参数固定,适用于平稳的随机信号,而实际上,语音是非平稳信号,因此在具体应用的过程中,受到限制;卡尔曼滤波要求参数是时变的,适应于非平稳信号,但其要求噪声和信号的统计特性是先验已知的;阀值去噪的关键在于如何选择阀值并进行阀值量化,阀值选取的好坏直接影响到信号消噪处理的质量.
由于语音信号在传输过程中具有一定的未知性,并且语音和噪声在统计特征上是相互独立的,本文将以此为依据,从盲源处理的角度,研究基于独立性特征的ICA(独立成分分析)语音除噪系统.
1 语音除噪ICA模型
ICA最先起源于“鸡尾酒会”问题[9],经过几十年的不断发展,ICA技术的应用领域涉及语音信号处理、机械信号处理、图形信号处理等.ICA技术能够成功应用的条件在于系统的物理模型在本质上与ICA数据处理模型一致.
假设有某个观测到的含噪语音变量x,x变量由1条语音信息s0和N个相互独立的噪声信号s1,…,sN线性组合得到,由于信号经过的信道、时延等的不同,噪声以及混合系数都是不确定的,则带噪语音信号的ICA模型可以描述为:
x=a0s0+a1s1+a2s2+…aNsN,
(1)
式中,aj,j=0,…,N是实向量系数,且式中只有观测变量x是已知的,语音和噪声以及他们的混合方式均为待估计的量.

图1 含噪观测语音信号滤波预处理框图
由于ICA处理数据时,需要采集多路并行的数据.假设将采集到的一路观测数据经过某一SIMO(单输入多输出)滤波系统,其传输函数为H,如图1所示.则信号x经过SIMO系统之后的输出Y为
(2)

现在问题的关键转化为如何寻找到这样的滤波函数族H,保证观测变量经过滤波器组之后依然包含所有的独立源成分.假设各滤波器的响应函数为:hi(t),i=1,2,…,N.yi代表观测经过第i个滤波器之后的输出,则
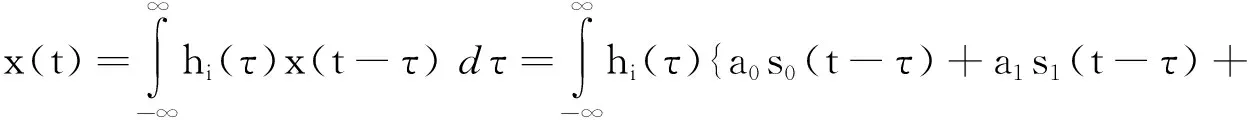
…aNsN(t-τ)}dτ,
(3)
输出变量yi,yj(i≠j)之间的相关函数可以表示为
Ryi,yj(t1,t2)=∬u,vhi(u)hj(v)E[{a0s0(t1-u)+…+aNsN(t1-u)}{a0s0(t2-v)+…+
由于si,sj之间相互独立,所以
E[si(t)sj(t)]=E[si(t)]E[sj(t)],

(4)
式中,Rsk为独立成分sk的自相关系数;Rsi,sj为独立成分si和sj之间的互相关系数,由于si和sj之间相互独立,所以肯定不相关,则Rsi,sj=0,式(4)转化为
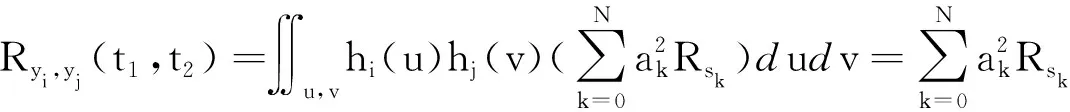
(5)
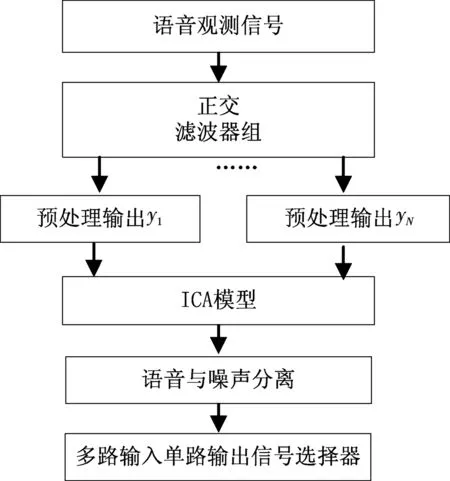
图2 语音除噪系统处理流程框图
当hi(t)与hj(t)为正交函数系时,∬u,vhi(u)hj(v)dudv=0,i≠j,从而使得Ryi,yj(t1,t2)=0,意味着此时的输出yi与yj是不相关的.对于标准正交滤波器,有∬hi(u)hi(v)dudv=1,所以系统输出信号的自相关系数是对应输入信号自相关系数的倍数关系,即Ryi ,yi(t1,t2) =ai2Rsi,滤波处理之后保留了所有源信号的独立成分.
以上分析表明,当让采集到的某单路语音混合信号经过一正交滤波器组时,输出信号将保留所有信号及噪声的独立成分,此时滤波器组的输出信号可以利用ICA数据处理模型进行描述.
2 基于ICA的语音除噪系统
对具体的语音除噪系统进行设计,其信号处理框图如图2所示.采集到的语音观测信号通过单路输入多路输出的标准正交滤波器组之后,得到N路输出,然后利用ICA技术,以最大化信号的独立性特征为目标,进行语音与噪声信号的分离,最后利用多路输入单路输出的信号选择器实现语音信号的除噪.

图3 语音除噪系统仿真
3 系统仿真分析
为了验证以上系统的除噪性能,对某预先录制好的纯净语音添加窄带噪声,利用以上所提出的语音除噪系统进行处理.在进行具体的信号处理时,滤波器组采用haar正交小波滤波器组进行信号预处理.在进行语音和噪声信号的分离时,由于其分离判据是最大化信号的独立性特征,而信号独立性特征较常用的度量参数为信息熵和峭度.本文为了简化计算,采用最大化信号的峭度进行.各阶段的信号波形如图3所示,图中(a)为未加噪声的纯净语音信号,(b)为添加了噪声的语音信号,(c)为除噪之后的语音信号.比较图(a)和(c)可知,除噪之后的信息保留了原信号的绝大部分信息,且除噪效果很好.
参考文献:
[1] 田玉静,左红伟,朱周华.LMS与RLS算法仿真消噪对比研究[J].通信技术, 2009,42(12):161-163.
[2] 丰明坤,李晓勇.基于小波变换的语音除噪虚拟仪器系统[J].语音技术,2006,9:54-55.
[3] 刘娟花,李福德.一种改进的小波域语音去噪方法研究[J].西安工程科技学院学报,2006,20(1):92-95.
[4] 任济生,任鹏,吉爱国.基于正交小波变换的自适应语音消噪改进方法[J].信息与控制,2007,36(4):501-505.
[5] 阮兆文.基于小波-卡尔曼的语音增强方法研究[J].通信技术.2010,43(4):152-154.
[6] 张亮,龚卫国. 一种改进的维纳滤波语音增强算法[J].计算机工程与应用2010,46(26):129-131.
[7] 尹伟,易本顺,沈小丰.有色噪声下基于Unscented粒子滤波的语音增强方法[J].电波科学学报.2009,24(3):476-481.
[8] 王继曾,王婵飞.基于最佳门限消噪语音增强一种新方法的研究与实践[J].计算机应用与软件.2009,26(1):253-254.
