平面上的强马尔科夫过程
2011-11-24杜保建何朝兵袁付顺
杜保建,何朝兵,袁付顺
(安阳师范学院数学与统计学院,中国 安阳 455000)
在马氏过程理论中,强马氏性是一个非常重要的基本概念.而两参数随机过程的强马氏性的时间变化分为随机的[1]和非随机的[2-5].文献[2,4~5]提出了宽过去强马氏性和平面上的*-强马氏性的一般定义.讨论了各种强马氏性之间的关系,这些强马氏性的参数变化是非随机的.对参数变化为随机的情况,至今还没有人研究.文献[7~10]研究了停点的各种定义及性质.由于两参数*-马氏过程具有良好的性质[6],所以本文对*-马氏过程提出参数变化为随机的*-强马氏过程的一般定义是十分必要的,本文还给出了*-马氏过程为*-强右选马氏过程的一个充分条件,研究了各种*-强马氏性之间的关系,创造性地推广了文献[1]中相应结果.

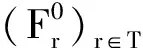
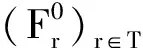
对r∈K-T,令Xr=c(E中某个固定点),可使X扩张定义于K上,对于(E,ε)上的*-转移函数(P1,P2,P)如下扩张定义于K上:

这样P(s,t,s′,t′,x,y,z,B)就定义在(s,t),(s′,t′)∈K,(s,t)≤(s′,t′),x,y,z∈E,B∈ε上,后面有时把P也记为P((s,t),(s′,t′),x,y,z,B),以后提到扩张到K上的(Xr)及P时,都是指上述扩张.
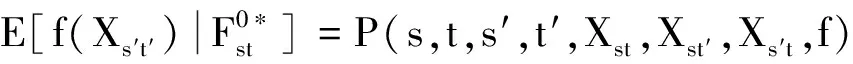



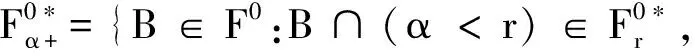
2 平面上*-强马氏性的一般定义

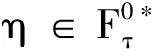
(1)对固定的B∈ε,映射(s,t,s′,t′,x,y,z)→P(s,t,s′,t′,x,y,z,B)为[B(K)]2×ε3可测的;

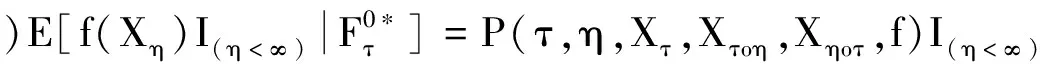
则称X为*-强μ0马氏过程.

(1)同定义1 中(1);


则称X为*-强右μ0马氏过程.

(1)同定义1 中(1);


则称X为*-强左μ0马氏过程.
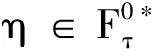
下面的定理1 给出了马氏过程为*-强右O0*马氏过程的一个充分条件.

则X是*-强右O0*马氏过程.


(1)
令
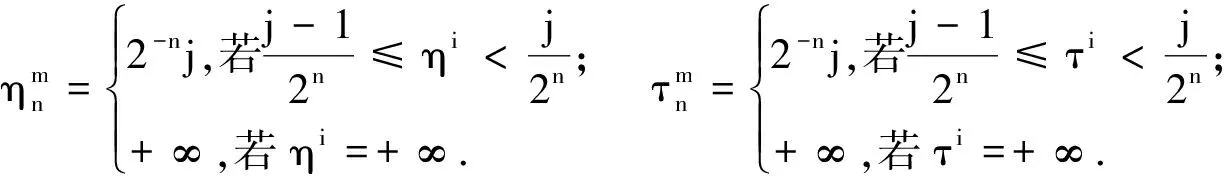
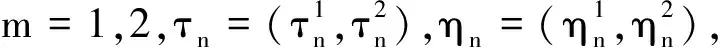

令n→+∞,由已知条件可得(1)式成立,由L-系方法可证对任意f∈bε,(1) 式也成立.
推论OUP2过程和右连续两指标独立增量过程都是*-强右O0*马氏过程.
由文献[1]和文献[6]给出的OUP2过程的*-转移函数和独立增量过程的*-转移函数可知P(s,t,s′,t′,x,y,z,B)关于(s,t,s′,t′,x,y,z)是连续函数,从而推论成立.


在完备化情况,定理1是*-强右选马氏性的一个充分条件,这时轨道在T上右连续可改为a.s.右连续.
为简单起见,下面只考虑完备化情况.
3 各种*-强马氏性之间的关系
由定义易证如下两个定理.
定理2设μ1和μ2是2个μ类函数集,μ1⊂μ2.则每个*-强(强左,强右)μ2马氏过程是*-强(强左,强右)μ1马氏过程.
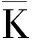
证因为X适应右连续,所以X宽过去循序可测,由文献[2]中定理3.1可知X具有*-强μ可测性.由定义2中强右μ马氏性得


与文献[1]中不同,对于τ∈O*,存在A,使τA为可及点和τAc为绝不可及点,但ηA不一定是可及点(当η=τ+(h,l)时成立,其中h>0,l>0为常数).因此,我们未能得到:X是*-强(强右)选马氏过程,当且仅当X同时为*-强(强右)及和*-强(强右)不及马氏过程.
参考文献:
[1] 侯 强.两指标马尔科夫过程的停点变换[J].西北电讯工程学院学报,1986(3):13-20.
[2] 周健伟.平面上的强Markov性[J].数理统计与应用概率,1994,9(4):78-83.
[3] 王梓坤.二参数ORNSTEIN-UHIENBECK过程[J].数学物理学报,1983,4(3):395-406.
[4] 周健伟.两指标过程的强马尔科夫性[J].应用概率统计,1986,2(4):302-306.
[5] 周健伟.两指标强马尔科夫过程[J].华东师范大学学报,1989,4(4):7-11.
[6] LUO S J.Two-parameter homogeneous Markovion processes[J].Acta Math Sci,1988,8(3):315-322.
[7] 杜保建.两指标过程的宽过去强Markov性[J].数理统计与应用概率,1995,10(4):25-30.
[8] 任晓红,陈慧婵,张卓奎.强鞅的停止性质[J].吉林大学学报:理学版,2003,41(2):463-465.
[9] 张卓奎,任晓红,陈慧婵.两指标停时及其性质[J].吉林大学学报:理学版,2002,40(2):127-130.
[10] 王生喜.N指标随机过程的停止[J].新疆大学学报:自然科学版,2003,20(1):26-28.
