高超声速飞行器自适应切换控制及稳定性分析*

2011-11-24谈树萍李智斌

空间控制技术与应用 2011年1期

关键词：超声速闭环飞行器

谈树萍，李智斌

(1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190)

高超声速飞行器自适应切换控制及稳定性分析*

谈树萍1，2，李智斌1，2

(1.北京控制工程研究所，北京100190；2.空间智能控制技术重点实验室，北京100190)

针对高超声速飞行器巡航段控制问题，构造自适应切换控制并对闭环稳定性进行了分析.高超声速飞行器动力学模型具有非线性、多变量和开环不稳定的特点.首先给出动力学模型局部线性化的方法，并设计自适应切换律和非线性反馈控制.进而给出全局稳定性分析结果，证明在所设计自适应切换控制下，闭环系统指数收敛到状态原点附近一个小邻域内.

高超声速飞行器；切换控制；自适应切换律；稳定性

本文符号

V：速度；T：推力；α：攻角；D：阻力；μ：地球引力常数；m：质量；γ：飞行路径角；h：高度；r：距地心距离；L：升力；q：俯仰角；Myy：俯仰力矩；Iyy：惯量矩；ρ：大气密度；S：参考面积；CL：升力系数；CD：阻力系数；CT：推力系数；R：地球半径；δe：舵面偏差；β：油门设置.

高超声速空天飞行器对于飞行条件和动力学参数的改变非常敏感，其轨迹与姿态高度耦合.气动参数并不是由舵偏角唯一确定，还受马赫数、攻角、侧滑角、角速度和大气环境等的影响，而且马赫数对气动参数的影响呈现出强非线性.由于以上原因，高超声速飞行器的动力学模型呈现出强非线性和强时变性.这些都加大了空天飞行器的控制难度.

对于空天飞行器这样的强时变和强非线性系统，自上世纪80年代，人们就开始研究其控制器设计方法［1-3］.在早期，主要是基于线性模型来设计控制律，如文献［4］假设所有状态是可量测的，只有小的传感器噪声污染，控制的目的是飞行器稳定以及高度精确的跟踪速度和高度命令信号，同时保证攻角偏差少于0.5o，并且使得控制能量最小化.考虑到空天飞行器是强非线性系统，随后人们主要针对非线性系统展开控制律设计，例如文献［5］基于非线性模型首先通过在某个工作点附近反馈线性化的方法，将非线性系统转化为等效的线性系统；随后，引入了自适应滑模控制设计方法，有效地处理参数的不确定性.由于高超声速飞行器的控制设计要求具有实时性，针对高超声速飞行器的爬升、巡航和再入段，国内学者基于特征模型和全系数自适应控制方法对控制器设计问题展开了深入的研究［6-8］.

为了能够设计在整个巡航阶段使得飞行器稳定的控制器，本文提出了针对不同工作点对系统线性化、通过切换工作点构造切换线性系统的方法，并随后通过闭环等价性，将原非线性系统控制器的构造问题转化为对等价的切换线性系统构造切换控制的问题.最后证明在本文设计的切换控制下系统的稳定性.

1 高超声速动力学模型

1.1 纵向动力学模型

现在文献中常见的高超声速飞行器的纵向模型多基于刚体假设，由关于速度V，飞行路径角γ，高度h，攻角α和俯仰角q的一组微分方程描述如下［9］：

式中：

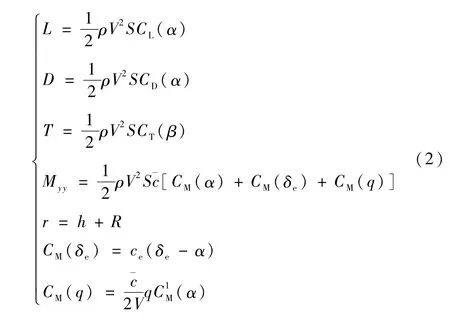
注1.式(2)中的各项参数主要是参考了文献［9］中给出的参数，但是考虑到 CL(α)，CD(α)，CT(β)，CM(α)，(α)等参数中涉及到的常系数，如0.6203等，实际上是在文献［9］中给出的标称工作点处系统对应的系数.我们这里考虑系统在整个巡航阶段不同工作点处的控制问题，涉及到的相应的系数的值应该是不同的，但是为了使本文的控制构造方法表达更加清晰，而不是陷入到关于各种变量的繁杂描述中，我们这里引用常系数来表明CL(α)等参变量关于系统状态α等的函数关系.如果要严格表明其在不同工作点关于α等的函数关系，应该表示如下：

发动机的动力学方程符合以下的二阶系统：

我们关心的输出项是高超声速飞行器的飞行高度及速度，这是通过飞行器的油门设置βc和俯仰控制舵面偏差δe来控制的.

假设1.时变参数 m，I，S，和 ρ可得.

这里我们考虑的是大气层内高超声速飞行器的巡航段，飞行高度大于 33.528km，小于39.624km［9］.在巡航过程中，高超声速飞行器的飞行速度很快，而攻角和飞行路径角相对而言非常小，从而我们可以引入如下的简化［9］：

地球引力常数μ=3.986005×1014，经过简单计算，可得

令

我们得到一个由7阶系统：

其中 X=［V，γ，h，α，q，β1，β2］T为系统状态，油门设置βc和舵面偏差δe为控制输入，速度V和高度h为输出变量，H(X)是由动力学方程(4)右端的非线性函数构成的7阶非线性函数矩阵，控制矩阵

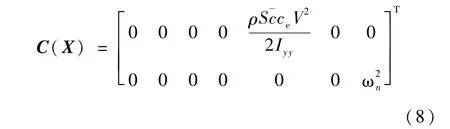
1.2 切换系统动力学模型

非线性函数矩阵H(X)关于函数变量X光滑.H(X)关于任意工作点X0的二阶泰勒展开为

式中：

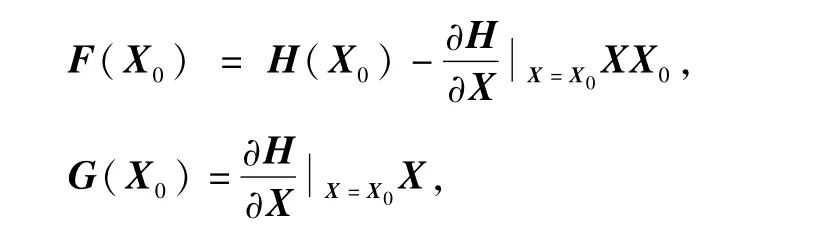
J(X0)ΔX] ，i=1，2，…，7.为Hession矩阵，=X0+θΔX，0≤θ≤1，ΔX=X-X0.容易计算得

其中，

根据方程(9)，非线性系统方程可改写为

实际上，二次型J(X0)表征非线性系统(10)在工作点X0附近的非线性程度，当非线性程度足够小时，J(X0)可视为系统扰动.

上述非线性系统在工作点X0附近的改写过程为整个巡航过程系统的改写提供了基本框架.在给出整个巡航段切换系统之前，我们首先介绍一下切换时刻、切换持续时间、切换频率和停留时间的概念.

定义1.考虑切换律σ(t)，对应于切换律 σ(t)的切换时刻0＜t1＜t2＜…定义为tk+1=inf{t＞tk：σ(t)≠σ(tk)}.切换持续时间δk定义为δk=tktk-1(k=1，2，…).切换频率 f定义为在区间［0，t］内的切换次数}.

停留时间定义为τ=in fkδk.

类似于在工作点X0附近的泰勒展开及非线性程度项的整合过程，对于一系列工作点Xσ(t)附近进行展开，系统 (7)可改写为切换系统：

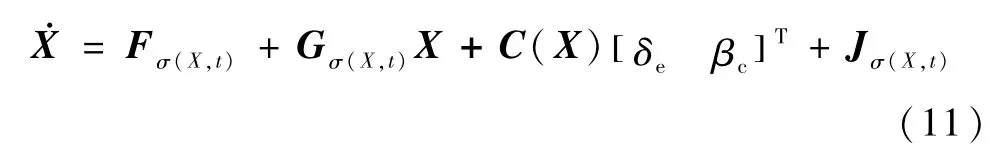
其中时刻 t0，t1，… 代表相应的工作时刻，即切换时刻.状态矩阵

其中，

注 2.为了简化符号，在本文随后部分将 a1，σ(X，t)简记为 a1，类似的将 a2，σ(X，t)简记为 a2， b2，σ(X，t)简记为b2，诸如此类.

2 自适应切换控制

高超声速飞行器动力学参数对飞行条件具有强耦合性.本文通过选择合适的控制向量［δeβc］T以保证整个巡航段飞行器的稳定控制.切换控制系统的控制性能依赖于切换时刻的选择和相应的工作点，考虑到二次型Jσ(X，t)表明了系统关于工作点的非线性程度，本节我们设计了与相关的在线自适应切换律σ(X，t)及相应的自适应非线性反馈控制.

首先给出如下引理.

引理1.当a2b3-b2a3≠0且c1a2+c2b2≠0时，切换系统 (11)的任一切换子系统能控.

证明.通过简单计算可得，当a2b3-b2a3≠0且c1a2+c2b2≠0时，

满秩，引理得证.

构造如下自适应切换控制律：

式中

自适应切换律满足：

σ(X，t)=

注3.存在这样的Xi+1满足条件(13).根据泰勒展开，Δ X，其中 Δ X=X-X0，X*=X0+θΔX，0≤θ≤1，H1(X*)是 Hession阵.

而HD是实对称矩阵：

对于二次型

其中，λ1，λ2，…，λ7是实对称矩阵HD的7个特征值，Q的7个列向量是HD属于λ1，λ2，…，λ7的7个单位正交的特征向量.对Hi()，我们设定阈值C0，对每一个若对应的说明系统在该工作点处的非线性程度满足控制器要求，否则需要切换工作点.

假设2.切换律 σ(X，t)：D×［t0，∞)→ Θ是分段常

值连续函数，其中Θ ={1，2，…，N}，N为正整数.在自适应切换控制(12)-(13)下，相应的闭环系统为

3 稳定性分析

引理 2［10］.假设矩阵 A∈ Rn×n，B∈ Rn×m满足系统(A，B)能控.那么，存在M＞0使得对任意λ＞0，存在矩阵K∈Rm×n使得以下不等式成立：

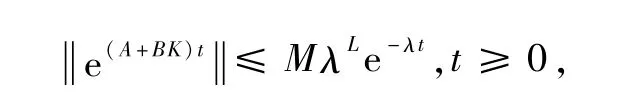
引理 3［10］.矩阵 Ai∈ Rn×n，Bi∈ Rn×m满足子系统(Ai，Bi)能控，则存在 M＞0，使得对任意 λ＞0，存在一组增益矩阵 Ki， i=1，…，7，使得

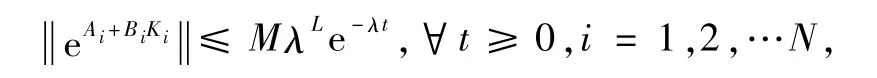
其中L=(n-1)(n+2)/2.

证明.据假设 1和引理 2，对 i=1，2，…N，存在 Mi＞0，使得对任意λ＞0，存在矩阵Ki∈Rm×n使得以下不等式成立：

定理1.当 a2b3-b2a3≠0且 c1a2+c2b2≠0时，对切换系统(11)及自适应切换控制(12)～(13)，如果对任意给定的常数ε，满足f≤ε，停留时间τ＞0，且存在有界常数C＞0使得≤ C，那么在切换自适应控制(12)～(13)下闭环系统稳定，且满足

其中

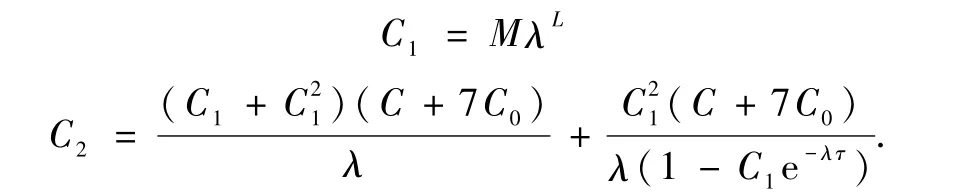
证明.根据引理3，对任意 λ＞0，存在一组反馈矩阵 Ki，i=1，…，7，满足

其中 M ＞0 是某个依赖于 {Gi，Bi，i=1，2，…N} 的常数.

对切换系统 (11)，假设初始时刻为 t0，系统初始状态为 X0，自适应切换时刻序列记为 t1，t2，…，tk，… .根据定义，对任意 t∈ ［tk，tk+1)，闭环系统记为

记Ak=Gk+BKk，则系统可改写为

求解微分方程(16)，解得

同理对 t∈ ［tk-1，tk) ，取 t=tk，可求解得 Xk：

递推解得

以及

根据引理3，可得如下不等式

从而

根据停留时间τ的定义，可得

记 C1=Mλ7，从而

其中μ=λ-(ln M+7 lnλ)(ε+1).

综合不等式(18)～(19)，即当λ足够大使得不等式

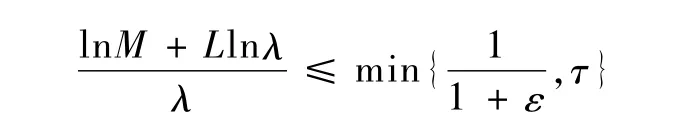
成立时，系统状态满足

不等式 (20)表明对足够大的时间t和参数λ，闭环系统(15)的状态变量指数收敛到状态原点附近的一个小邻域内，定理得证.

4 结论

本文针对高超声速飞行器这一具有强非线性和强时变性的动力系统，通过在工作点附近线性化系统并切换工作点的方式得到了切换线性系统，并证明了与切换系统各子系统闭环等价的线性系统能控，而且针对闭环后等价的切换系统设计了切换控制，证明了原系统在此切换控制下状态的稳定性.

需要指出的是，本文假设工作点切换持续时间的上确界为有限常数，且系统线性化后得到的常矩阵和有界噪声满足一定的一致有界性，这些条件相对比较苛刻，还需要在进一步的工作中弱化或去掉.并且如何获得切换工作点的系统参数也是在设计控制器过程中需要进一步解决的问题.

［1］Mooij E.Numerical investigation of model reference adaptive control for hypersonic aircraft［J］.Journal of Guidance， Control， and Dynamics，2001，24(2)：315-323

［2］Chuang C H，Morimoto H.Sub-optimal and optimal pe-riodic solutions for hypersonic transport［C］.ACC，Seattle，Washington，1995

［3］Dewell L D，Speyer J L.Fuel-optimal periodic control and regulation in constrained hypersonic flight［J］.Journal of Guidance， Control， and Dynamics，1997，20(5)：923-932

［4］Gregory IM，Chowdhry R S，McMinn JD，et al.Hypersonic vehicle model and control law development usingH∞andμsynthesis［R］.NASA TM-4562，1994

［5］Kuranov A，Korabelnikov A.Hypersonic technologies of atmospheric cruise flight under AJAX concept［C］.The 15thAIAA International Space Planes and Hypersonic Systems and Technologies Conference， Dayton， Ohio，2008

［6］吴宏鑫，孟斌.高超声速飞行器控制研究综述［J］.力学进展，2009，39(6)：756-765

［7］孟斌，吴宏鑫，林宗利，等.基于特征模型的 X-34爬升控制设计［J］.中国科学(F辑)，2009，39(11)：1202-1209

［8］杨俊春，胡军，倪茂林.基于特征模型的再入飞行器自适应制导律设计［J］.中国科学(E辑)，2008，38(12)：2134-2149

［9］Xu H J，Mirmirani M D，Loannou P A.Adaptive sliding mode control design for a hypersonic flight vehicle［J］.Journal of Guidance， Control， and Dynamics，2004，27(5)： 828-838

［10］Cheng D Z， Guo L， Lin Y，et al.Stabilization of switched linear systems［J］.IEEE Transactions on Automatic Control， 2005，50(5)： 661-666

［11］Cheng D Z， Guo L， Lin Y，et al.A note on overshoot estimation in pole-placement［J］.Journal of Control Theory Application， 2004，2(2)：161-164

Sw itching Control Design for a Hypersonic Flight Vehicle

TAN Shuping1，2， LI Zhibin1，2
(1.Beijing Institute of Control Engineering， Beijing 100190， China；2.Science and Technology on Space Intelligent Control Laboratory， Beijing 100190， China)

An adaptive switching controller is designed and analyzed for the longitudinal dynamics of a generic hypersonic flight vehicle in the whole cruise phase rather than a trimm ing condition.Thismodel is nonlinear，multivariable and unstable.The adaptive controller presented in this paper consists of a local linearization method， an adaptive switching law and a nonlinear feedback control law.Furthermore， it is obtained that the closed-loop system is stable under the adaptive switching control.

hypersonic flight vehicle； switching control； adaptive switching law；stability