利用神经网络建立GPS网络RTK的双差对流层误差模型*

陈远鸿 邱 蕾 冯玉钊

(1)深圳市勘察研究院有限公司，深圳 518026 2)深圳市地籍测绘大队，深圳518000)

利用神经网络建立GPS网络RTK的双差对流层误差模型*

陈远鸿1)邱 蕾2)冯玉钊2)

(1)深圳市勘察研究院有限公司，深圳 518026 2)深圳市地籍测绘大队，深圳518000)

为减小对流层误差改正数中系统偏差的影响以提高对流层改正精度，提出了基于神经网络的顾及空间的对流层误差建模模型，该模型的对流层延迟误差改正在网内外精度均达5 cm。

GPS;网络RTK;对流层误差;神经网络;高程差异

1 前言

网络RTK中GNSS数据处理的关键问题包括基准站间双差模糊度的确定、流动站误差计算与消除和流动站模糊度的确定。流动站对流层误差的准确建模是其中一个关键问题。目前，常用的网络内插模型主要是线性内插模型，该模型的本质是在平面内建立对流层误差模型，然后进行内插得到流动站的误差信息，同时模型的建立至少需要3个参考站。对流层延迟误差受高程影响比较显著，使得对流层误差在水平方向和高程方向空间相关特性存在明显差别，将上述模型直接应用于对流层延迟误差改正时，由于仅仅在平面上建立对流层误差模型，因此会引入高程方向的系统性偏差。

本文提出了基于神经网络的空间对流层误差建模模型，该对流层误差模型不仅考虑了平面位置关系，同时考虑了高程因素的影响，基于空间因素对对流层进行建模，并且建模时只需要两个参考站，因此，对于地形变化比较大的地区，应用该方法获得流动站对流层的延迟改正信息，精度可以得到相应的提高。

2 网络RTK对流层改正信息的提取

在网络RTK中，由于参考站的精确参考站坐标已知，因此可以利用宽巷较长的波长特性，在短时间内固定双差整周模糊度。然后把宽巷整周模糊度引入无电离层组合观测方程中，用动态卡尔曼滤波，估计出L1和L2上的整周模糊度和相应的天顶距对流层延迟。L1载波的卡尔曼滤波模型在状态向量包括L1双差模糊度▽ΔNm，主参考站ZTDa的天顶方向延迟，副参考站ZTDb的天顶方向延迟，其状态向量为：

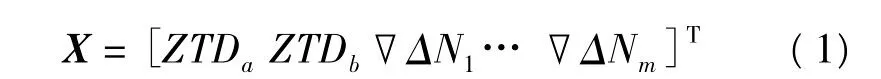
设L1双差模糊度参数的个数为m，则状态参数的总数为2+m。以任一卫星i的载波相位的观测方程设计矩阵为：

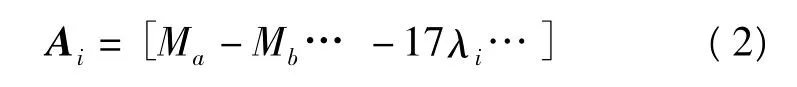
式中，Ma表示主参考站a上卫星对应的对流层延迟投影函数值，Mb表示副参考站b上卫星对应的对流层延迟投影函数值，λi表示卫星i的无电离层组合观测值的波长。其状态转移矩阵为：

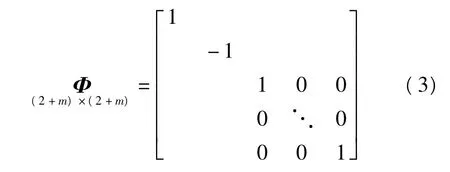
式中Φ矩阵中的空白位置均为0。对流层延迟采用随机游走法，通过卡尔曼滤波进行估计，状态噪声协方差阵为：

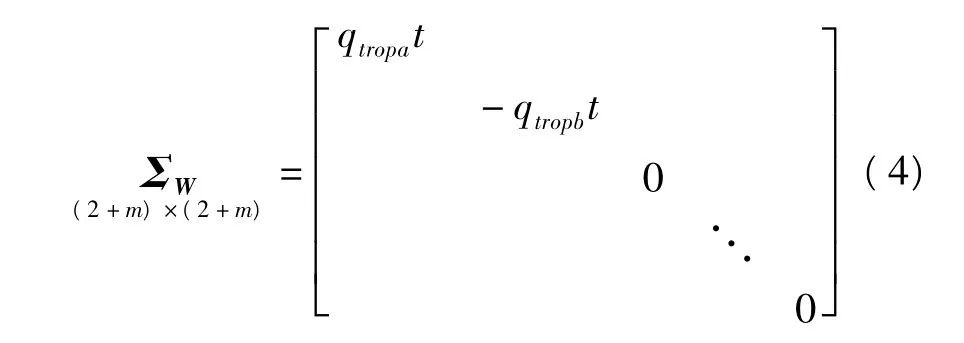
式中，qtropa、qtropb表示对流层延迟的谱密度。ΣW矩阵中的空白位置均为0。

在估计出主参考站a和副参考站b的天顶距对流层延迟后，网络基线上任意时刻双差对流层延迟Δ▽可以表示为天顶距对流层延迟与其映射函数的乘积，如：

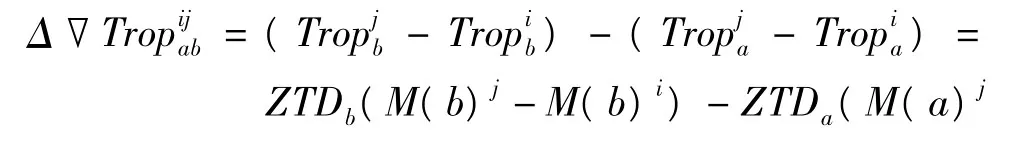
式中i为参考卫星，j为流动卫星，M(b)j为参考站b上的j号卫星的映射函数。

3 对流层高程方向的偏差

对流层延迟误差不但受水平因子的影响，而且还受高程因子的影响。当流动站在水平方向强约束于参考站所构成的区域内时，在高程方向却可能远离模型区域内插面。由于高程因子影响，使由平面坐标参数估算的模型内插值与移动用户所在高程位置上的对流层延迟真值间存在不符值，或称为高程方向偏差［8］。

为了分析对流层在高程方向的影响，选取1个测区进行实验(图1)。测站的经度、纬度和高程分布如图2所示。利用分段线性法以一个小时为间隔计算出各条基线的双差对流层延迟，分别将6个测站2个时段的对流层延迟绘制于图2(d)。

图1 点位分布Fig.1 Distribution of stations

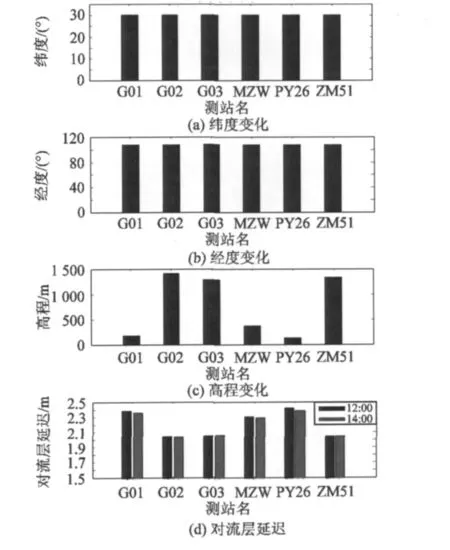
图2 测站信息Fig.2 Information of stations

从图2可以看出，单站对流层延迟都在2 m以上。6个测站的经度和纬度比较接近，但是地形起伏比较大，高程最小的点PY26与高程最大的G02，高程相差1 100 m，单站对流层延迟相差也达到了0.4 m，G02、G03、ZM51 3个点的高程比较接近，相差在100 m左右，单站对流层影响相差比较明显，G01、ZM51、PY26 3个点的高程均在500 m以下，图2(d)中3个点的对流层延迟相差不明显。因此对流层延迟值与测站的高程有较强的相关性，高程越大，对流层延迟越小。对于地势越低的地方，高程方向的影响比地势高的地方影响大，对流层延迟值与测站的高程有一定的相关性，对于连续时间段内，对流层延迟相差比较小，差别只有厘米级。

4 基于神经网络的区域对流层模型的建立

神经网络模型在理论上可以无限逼近任意复杂的曲面，因此可以很好地拟合对流层延迟变化。此外，神经网络具有较好的预测能力，可以满足网络RTK实时播发对流层改正数的需要。对于双差残余对流层延迟，只需要利用两个参考站之间的历元时刻、卫星的方位角双差、X方向的方向余弦、Y方向的方向余弦、Z方向的方向余弦5个输入量，用神经网络技术来拟合区域对流层模型，从而实时播发对流层延迟改正数。计算步骤为：

1)选取合适的主参考站和一个副参考站，利用式(5)估计出主副参考站之间的双差对流层残余延迟;

2)将历元时刻、卫星的方位角双差、X方向的方向余弦、Y方向的方向余弦、Z方向的方向余弦作为神经网络的输入信号，对应的对流层延迟作为期望输出信号，采用3层BP神经网络模型，使用LM算法进行网络训练就可以得到基于神经网络的对流层模型;

3)保存神经网络的网络结构和各个网络权值，作为双差对流层改正模型;

4)输入流动站和主参考站的历元时刻、卫星的方位角双差、X方向的方向余弦、Y方向的方向余弦、Z方向的方向余弦5个量来获取流动站的对流层延迟改正量。

5 试验及结果分析

实验数据与图1的试验数据一样，数据采样率为15 s，点位分布如图1所示。计算采用网络中部分网形，选取MZW，G01，ZM51站作为计算推值的参考点，G02站作为主参考站，G03为副参考站。以一个小时的双差对流层残余延迟建立BP神经网络区域对流层模型。神经网络结构为：5个输入神经元，8个隐层神经元和1个输出神经元，设置最大迭代次数为150次，迭代终止误差为0.000 01 m。输出神经元的激活函数为线性函数，隐层激活函数选取tanh函数：

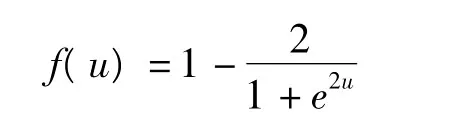
1)内符合精度检查

利用G02、G03一小时的双差对流层延迟进行训练，图3绘制了BP神经网络模型的1小时训练残差，其小时的训练残差基本都在1 cm以内。

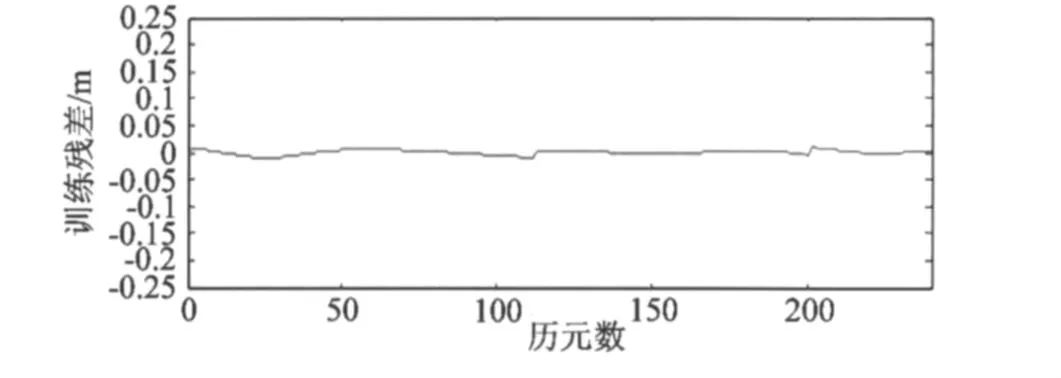
图3 BP神经网络模型的1个小时的训练残差Fig.3 Residual error plot of BP

2)外符合精度检查

利用G02、G03一小时的双差对流层延迟进行训练，图4～6绘制了基线 G02-G01、基线 G02-ZM51、基线G02-MZW的BP神经网络模型的1个小时的拟合值(240个历元)，并且预报了20个历元(5分钟)的对流层延迟量。

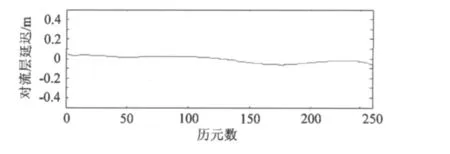
图4 基线G02-G01双差残余对流层延迟Fig.4 Residual double-tropospheric delay for G02-G01

图5 基线G02-ZM51双差残余对流层延迟Fig.5 Residual double-tropospheric delay for G02-ZM51

从图4～6可以看出，BP神经网络拟合的双差对流层残余延迟量都在5 cm内，在第240个历元(1小时后)预报5分钟的双差残余对流层延迟量与真值差别也在5 cm内，模型比较稳定;双差对流层残余延迟量呈线性变化，3条基线中G02-G01的高差最大，双差残余对流层延迟的变化最大，基线G02-ZM51的高差最小，双差残余对流层延迟的变化最小。

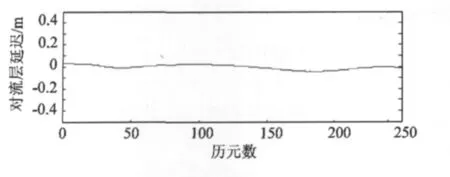
图6 基线G02-ZM51双差残余对流层延迟Fig.6 Residual double-tropospheric delay for G02-ZM51

3)与线性内插法进行比较

为了便于比较，选取G02为主参考站，MZW、ZM51、G03为副参考站，外推G01的双差残余对流层延迟与真值进行比较结果见图7。图中最大差值为-0.073 m，与图4中5cm的精度相比，BP神经网络拟合的对流层模型提高了2 cm。

图7 基线G02-G01双差残余对流层延迟Fig.7 Residual double-tropospheric delay for G02-G01

6 结束语

通过分析可以得出：网络RTK中，对流层延迟与高程密切相关;利用BP神经网络建立区域对流层模型仅需要两个参考站中1小时的双差残余对对流层延迟进行改正，这对于连续运行的网络CORS站是可行的。同时基于BP神经网络的区域对流层模型考虑了对流层在空间上的分布，使得网络RTK对流层延迟改正精度可达5 cm内，并且对于网内和网外的改正精度一样，同时可以预报5分钟的双差残余对流层改正，能够满足实时定位的要求。

1 Liwen Dai，et al.A study on GPS/GLONASS multiple reference station techniques for precise real-time carrier phasebased positioning［A］.ION GPS2001［C］.Salt Lake City：Palm Springs，2001：392-403.

2 王琛.基于Levenberg-Marquardt算法的用户鉴别［J］.山西师范大学学报(自然科学版)，2005，19(2)：17-20.(Wang Chen.The authentication of the computer users based on Levenberg-Marquardt algorithm［J］.Journal of Shanxi Teachers University(Natural Science Edition，2005，19(2)：17-20)

3 熊永良，等，基于多个GPS基准站的对流层延迟改正模型研究［J］.工程勘察，2005，(5)：55-57.(Xiong Yongliang，et al.Study of tropospheric delay correction model based on multiple GPS stations［J］.Geotechnical Investigation＆Surveying，2005，(5)：55-57)

4 王勇，张立辉，杨晶.基于BP神经网络的对流层延迟预测研究［J］.大地测量与地球动力学，2011，(3)：134-137.(Wang Yong，Zhang Lihui and Yang Jin.Study on perdiction of zenith tropospheric delay by use of BP neural network［J］.Journal of Geodesy and Geodynamics，2011，(3)：134-137)

5 徐韶光，等.长距离动态GPS数据处理在地震监测中的应用研究［J］.测绘科学，2011，36(2)：88-90.(Xu Shaoguang，et al.Applied research of long range kinematic GPS data processing in seismic monitoring［J］.Science of Surveying and Mapping，2011，36(2)：88-90)

6 陈中新，朱丽强.区域气象特征对流层延迟模型的建设研究［J］.城市勘测，2010，(4)：93-96.(Chen Zhongxin and Zhu Liqiang.Research on the modeling of tropospheric delay based on a region atmosphere features［J］.Urban Geotechnical Investigation＆Surveying，2010，(4)：93-96)

7 高星伟，等.WAAS对流层延迟模型及其在网络RTK中的应用［J］.测绘科学，2011，36(3)：82-84(Gao Xingwei，et al.WAAS troposheric delay model and its application in network RTK［J］.Science of Surveying and Mapping，2011，36(3)：82-84)

8 杨汀.网络RTK定位精度影响因子与GNSS数据网络传输研究［D］.中国矿业大学(北京)，2010.(Yang Ding.Research on the affected factors of positioning accuracy and network transmission of GNSS data in network RTK［D］.China University of Mining and Technology(Beijing)，2010)

A TROPOSPHERIC DELAY MODEL FOR GPS NET RTK ESTABLISHED BY USE OF ARTIFICIAL NEURAL NETWORK

Chen Yuanhong1)，Qiu Lei2)and Feng Yuzhao2)

(1)Shenzhen Investigation＆Research Institute Co.，Ltd.，Shenzhen 518026 2)Shenzhen Cadastral Surveying and Mapping Office，Shenzhen518034)

In the Virtual Reference Station(VRS)technology，atmospheric refraction error is the main factor affecting the accuracy of the long-distance RTK.However，the elevation difference between the reference plane and the roving station will cause the deviation of tropospheric error in the system and then the accuracy of troposphere correction will be lowered.A new tropospheric error model based on neural network，taking into account the space troposphere error，is presented.The accuracy of tropospheric delay model is within 5 cm，in spite of interpolation points in the network or out of network.

GPS;network RTK;tropospheric error;neural network;elevation difference

1671-5942(2011)06-0128-04

2011-07-12

陈远鸿，男，1981年生，工程师，从事GNSS数据处理及相关测绘工作.E-mail：elalei7630@163.com

P207

A