全缘叶绿绒蒿挥发性组分定量结构-色谱保留关系研究
2011-11-23兰作平廖立敏
兰作平,廖立敏,刘 宇,余 瑜*
1重庆医科大学药学院,重庆400016; 2重庆医药高等专科学校,重庆400030;3内江师范学院资源与环境科学学院,内江641112
全缘叶绿绒蒿挥发性组分定量结构-色谱保留关系研究
兰作平1,2,廖立敏3,刘 宇1,余 瑜1*
1重庆医科大学药学院,重庆400016;2重庆医药高等专科学校,重庆400030;3内江师范学院资源与环境科学学院,内江641112
提出顶点及顶点相互作用矢量的概念,并将该矢量用于复杂样本的分子结构表征。采用逐步回归结合统计检测对变量进行筛选后,再用多元线性回归建立了定量结构-色谱保留(QSRR)关系的7变量模型,模型的建模计算值复相关系数(R)为0.990,标准偏差(SD)为1.325;留一法(LOO)交互检验复相关系数(RCV)为0.983,标准偏差(SDCV)为1.696。结果表明该矢量具有较强的分子结构表达能力,模型具有良好的估计能力与稳定性。
全缘叶绿绒蒿;挥发性有机物;结构描述子;定量结构色谱保留相关
分子结构与色谱保留之间的定量关系的构建,需要引入相应的结构描述子。长期以来,研究者们在这方面已经做了许多有意义的工作。例如利用分子的几何结构、拓扑性质及连接特征和各种物化参数等进行结构描述,然后建立QSRR模型来预测化合物的色谱保留值[1,2]。全缘叶绿绒蒿(Meconopsis integrifolia Franch.)又称绿绒蒿,系罂粟科绿绒蒿属一年生草本植物,分布于甘肃、青海、西藏等省区。全缘叶绿绒蒿可以应用于食品及药品,具有清热止咳的功效,藏医用其花治疗肝热病和肺热病。最近官艳丽等[3]采用水蒸气蒸馏法提取出了全缘叶绿绒蒿花精油,用GC-MS法分离并分析鉴定其成分,最后鉴定出55个挥发性化学成分(表1)。这些化合物包括烷烃、环烷烃、烯烃、芳烃、醇、酯等,并且还含有N、O、S等杂原子,因此分子的元素组成复杂及结构跨度大,我们称之为复杂样本。本文根据有机化合物分子的隐氢图,提出顶点及顶点相互作用矢量的概念,为验证该矢量在分子结构表征上的普适性,采用由此55种物质组成的复杂样本进行建模研究。借助逐步回归、多元线性回归和留一法交互检验建立了7变量的分子结构与气相色谱保留值之间的相关模型(QSRR),取得较好的结果,可望为天然药物及精细化工产品的色谱行为提供有益参考。
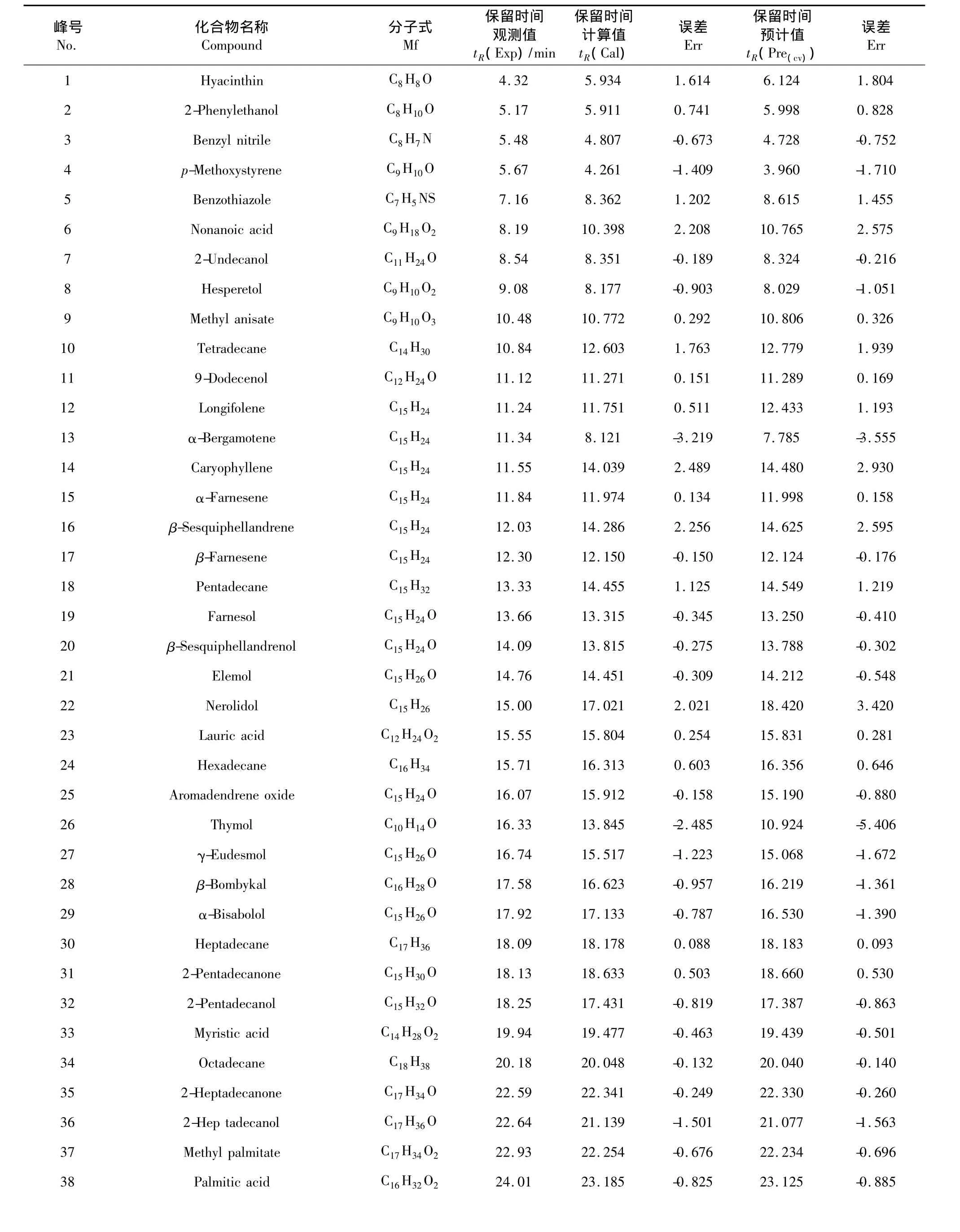
表1 55个化合物及其保留时间Table 1 Fifty-five components and their retention times
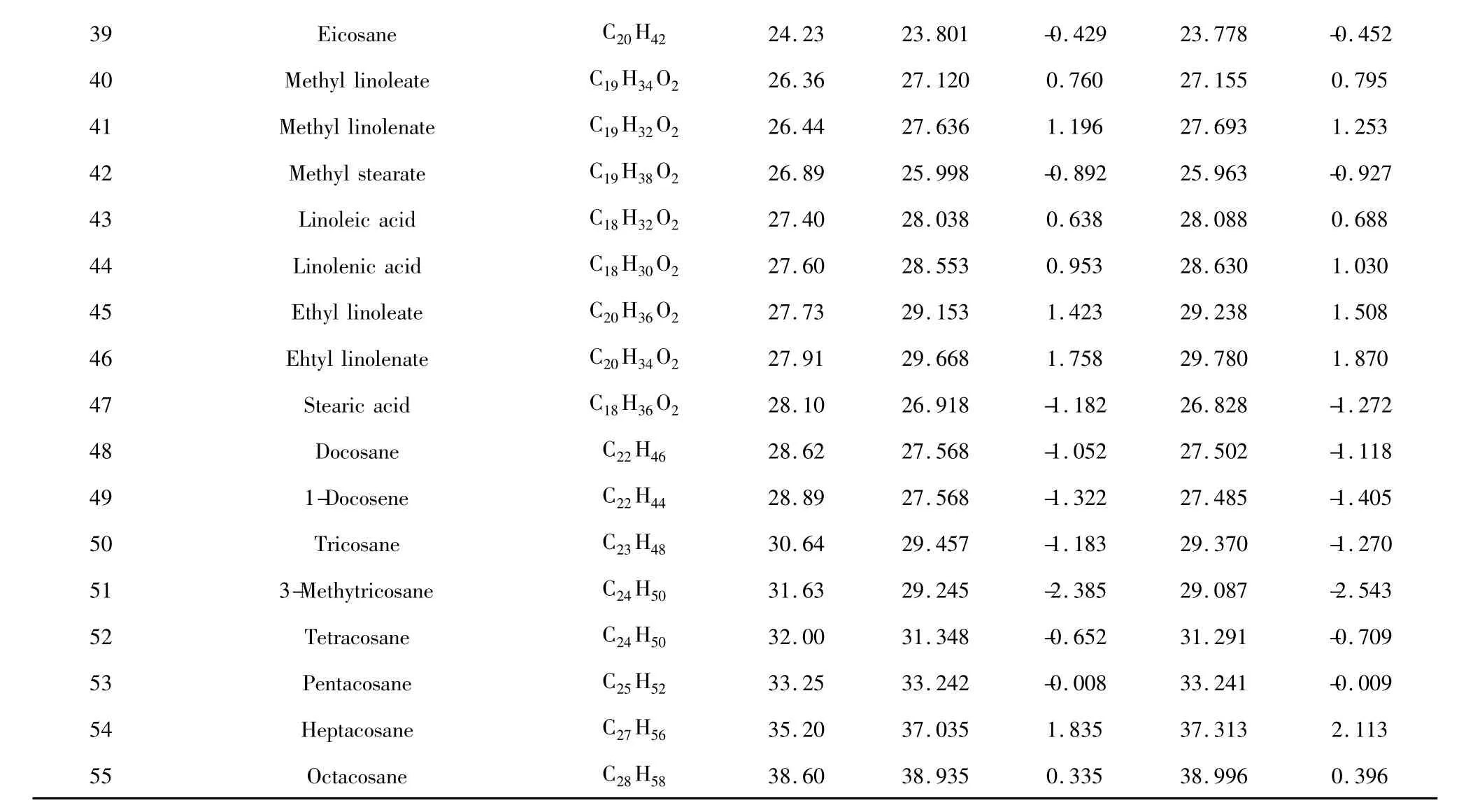
3 9 E i c o s a n e C 20 H 42 2 4.2 3 2 3.8 0 1 -0.4 2 9 2 3.7 7 8 -0.4 5 2 4 0 M e t h y l l i n o l e a t e C 19 H 34 O 2 2 6.3 6 2 7.1 2 0 0.7 6 0 2 7.1 5 5 0.7 9 5 4 1 M e t h y l l i n o l e n a t e C 19 H 32 O 2 2 6.4 4 2 7.6 3 6 1.1 9 6 2 7.6 9 3 1.2 5 3 4 2 M e t h y l s t e a r a t e C 19 H 38 O 2 2 6.8 9 2 5.9 9 8 -0.8 9 2 2 5.9 6 3 -0.9 2 7 4 3 L i n o l e i c a c i d C 18 H 32 O 2 2 7.4 0 2 8.0 3 8 0.6 3 8 2 8.0 8 8 0.6 8 8 4 4 L i n o l e n i c a c i d C 18 H 30 O 2 2 7.6 0 2 8.5 5 3 0.9 5 3 2 8.6 3 0 1.0 3 0 4 5 E t h y l l i n o l e a t e C 20 H 36 O 2 2 7.7 3 2 9.1 5 3 1.4 2 3 2 9.2 3 8 1.5 0 8 4 6 E h t y l l i n o l e n a t e C 20 H 34 O 2 2 7.9 1 2 9.6 6 8 1.7 5 8 2 9.7 8 0 1.8 7 0 4 7 S t e a r i c a c i d C 18 H 36 O 2 2 8.1 0 2 6.9 1 8 -1.1 8 2 2 6.8 2 8 -1.2 7 2 4 8 D o c o s a n e C 22 H 46 2 8.6 2 2 7.5 6 8 -1.0 5 2 2 7.5 0 2 -1.1 1 8 4 9 1 -D o c o s e n e C 22 H 44 2 8.8 9 2 7.5 6 8 -1.3 2 2 2 7.4 8 5 -1.4 0 5 5 0 T r i c o s a n e C 23 H 48 3 0.6 4 2 9.4 5 7 -1.1 8 3 2 9.3 7 0 -1.2 7 0 5 1 3 -M e t h y t r i c o s a n e C 24 H 50 3 1.6 3 2 9.2 4 5 -2.3 8 5 2 9.0 8 7 -2.5 4 3 5 2 T e t r a c o s a n e C 24 H 50 3 2.0 0 3 1.3 4 8 -0.6 5 2 3 1.2 9 1 -0.7 0 9 5 3 P e n t a c o s a n e C 25 H 52 3 3.2 5 3 3.2 4 2 -0.0 0 8 3 3.2 4 1 -0.0 0 9 5 4 H e p t a c o s a n e C 27 H 56 3 5.2 0 3 7.0 3 5 1.8 3 5 3 7.3 1 3 2.1 1 3 5 5 O c t a c o s a n e C 28 H 58 3 8.6 0 3 8.9 3 5 0.3 3 5 3 8.9 9 6 0.3 9 6
1 原理与方法
在有机化合物分子的隐氢图中,每一个非氢原子即为分子顶点。我们认为整个有机物分子的性质与分子顶点本身及顶点之间的相互作用存在密切关系,而分子中的非骨架氢原子对整个分子性质的影响可以忽略不计。并且不同类型的分子顶点及顶点之间的相互作用对分子性质的贡献不同,同类型的分子顶点及顶点之间的相互作用对分子性质的贡献具有加和性。因此我们首先需将分子内的非氢原子进行分类,分子内的非氢原子依据其所连接的其它非氢原子数分为A1、A2、A3、A4四类,分别表示与1、2、3、4个其它非氢原子相连,如与两个非氢原子相连的仲碳原子属于A2原子类型。
对于分子顶点本身对分子性质的贡献。本文引入了Hall和Kier[4]所提出的原子固有状态(I),并对文献的计算方法进行了一定的修正,得到了所谓的分子顶点矢量,用于表征分子顶点自身的状态对分子性质的影响。其计算式如下:
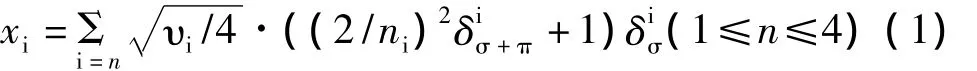
上式中,xi表示分子中顶点原子类型为i的所有顶点原子的贡献值,νi是顶点原子类型为i的原子价电层的电子数;ni为该原子价电层所属的主量子数是该原子参与成σ和π键的总电子数为成σ键的电子数。如单个CSP、、在分子中的顶点贡献值分别是2.5000、1.6667、1.2500。根据顶点原子的分类,分子中最多含四类原子,则每个分子将最终得到四个顶点矢量,分别记为x1、x2、x3和x4。
对于分子顶点间的相互作用对分子性质的贡献。顶点之间的相互作用与顶点原子电性及相隔距离密切相关。一般而言,依据库仑定律,电性越大、距离越小,相互作用就越大。本文借鉴文献[5-8]的表征方法来表征分子顶点间的相互作用对分子性质的贡献,即化合物分子中四类顶点原子发生相互作用可以组合出以下几种方式:m11、m12、m13、m14、m22、m23、m24、m33、m34、m44,分别记为x5、x6、x7、x8、x9、x10、x11、x12、x13、x14十个顶点相互作用矢量。各元素可按下式计算:
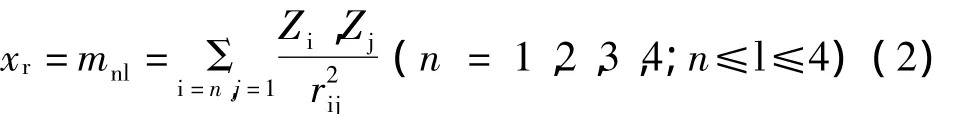
Z为顶点原子相对于C原子的相对电负性,如O的相对电负性为3.44/2.55=1.3490;rij是原子i、j之间的相对距离(即所经最短途径相对于碳碳单键的相对键长之和),n和l为原子所属类型。
这样对于每一个有机化合物分子,将有十四个变量来描述其结构信息。与文献[5-8]相比,像CH4、NH3等只有单个顶点的分子结构信息将可以得到表达。将样本分子的顶点原子按原子属性及连接方式输入到自编C语言程序加以处理,得到所有样本分子的十四个矢量值。
2 结果与分析
由于变量数较多,并且变量之间可能存在着共线性,因此对变量进行筛选并且使样本数/变量数符合N/n≧5的经验规则,寻找最佳变量组合就显得尤为必要。本文采用SPSS统计处理软件对变量作逐步回归(SMR)分析。为控制模型稳定性和消除变量间共线性影响,对每步变量计算方差膨胀因子(VIF)[9]。VIF定义为:VIF=(1-r2)-1,式中r为某自变量与其他变量相关程度(经自由度校正)。VIF为1.0,表示各变量间无相关性;VIF值在1.0~10.0间,表示变量间无明显共线性,相关方程可接受;VIF值大于10,相关方程不可靠。
逐步回归(SMR)分析发现当7个变量入选模型时,建模复相关系数R、标准偏差SD、留一法交互检验复相关系数RCV及标准偏差SDCV同时达到理想值,此时变量之间也不存在明显共线性(VIF最大值为9.90),并且符合N/n≧5的经验规则。7变量模型如下:
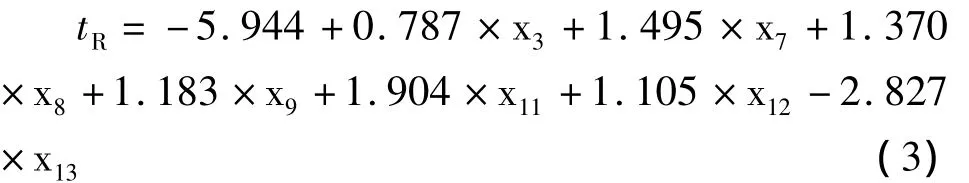
模型拟合:n=55,m=7,R=0.990,SD= 1.325,FM1=324.673;
LOO检验:RCV=0.983,SDCV=1.696,FCV= 195.533

图1 模型估计及预测值与实验值相关图Fig.1 Plot of estimated values and predicted values vs.experimental values
化合物的色谱保留时间与顶点间的相互作用存在良好的线性关系[8,10],而本研究中顶点矢量及顶点相互作用矢量在模型中均有体现,并且发现在逐步回归中x11首先被引入模型,说明化合物的色谱保留时间的确也受到分子顶点自身所处状态的影响。而上述模型对所有样本在文献所述条件下的气相色谱保留时间进行了估计和预测,结果列于表1的Cal及Pre(cv)栏。模型估计值及留一法交互检验值对实验值作图及残差分布分别见图1及图2。
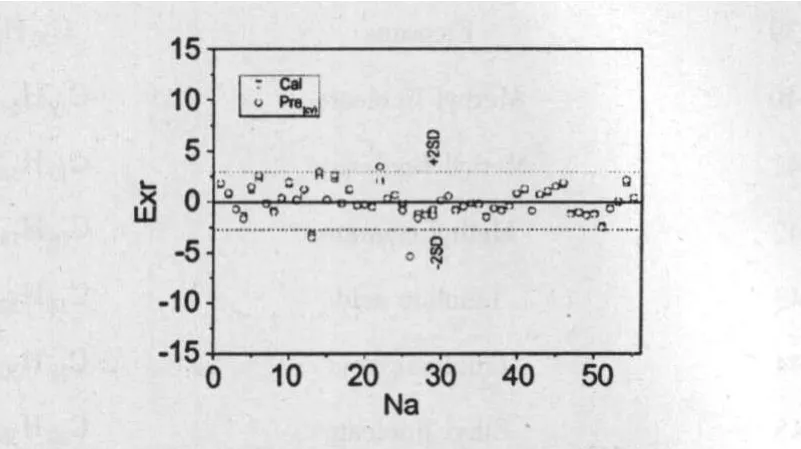
图2 模型估计及预测误差分布图Fig.2 Plot of estimated and predicted residuals scattered
由图1可以看出,几乎所有样本点都落在45°的对角线上或附近,由图2容易发现大部分样本点的估计与留一法检验误差落在2SD(图中虚线)以内。在模型拟合中只有1个样本点(1.8%)、留一法交合检验中只有4个样本点(7.3%)落在2SD外,说明模型的具有良好的稳定性和预测能力,估计的准确性较高。需要进一步说明的是,本文所研究的样本为来自天然产物的复杂样本体系,分子结构跨度大(包括烷烃、环烷烃、烯烃、醇、酸和酯等,并且还含有N、O等杂原子)。对于这样复杂的样本,本文所取得的结果应是满意的。
3 结论
化合物在色谱柱上的保留行为与它们同固定相之间的相互作用有关。当固定相一定时,这种相互作用的程度大小将直接与化合物的组成、化学结构、键合状态和电性特征相关。从本文的研究结果可以看出,提出的顶点及顶点相互作用矢量能很好地表征化合物的组成、化学结构、键合状态和电性特征。描述参数取值完全来自分子本身,具有计算过程简单,结果精度高等优点。本文取得的良好结果对于天然药物中挥发性有机化合物等复杂样本的QSRR研究具有一定的参考价值。
1 Zhou P(周鹏),Mei H(梅虎),Tian FF(田菲菲),et al.Novel generalized correlative index used to carry out research in Quantitative Structure-retention Relationship for some persistent organic pollutants.Chin J Anal Chem(分析化学), 2006,34:1096-1100.
2 Zhang T(张婷),Liang YZ(梁逸曾),Zhao CX(赵晨曦),et al.Prediction of temperature-programmed retention indices from molecule structures.Chin J Anal Chem(分析化学),2006,34:1607-1610.
3 Guan YY(官艳丽),Dawa ZM(达娃卓玛),Gesang SL(格桑索朗),et al.Study on essential oil from flowers of Meconopsis integrifolia.Chin Pharm J(中国中药杂志),2007,42:539-540.
4 Hall LH,Kier LB.Electrotopological state index for atom types:a novel combination of electronic,topological,and valence state information.J Chem Inf Comput Sci,1995,35: 1039-1045.
5 Liu SS,Yin CS,Cai SX,et al.Molecular structural vector description and retention index of polycyclic aromatic hydrocarbons.Chem Intell,2002,61:3-15.
6 Sun LL,Zhou Y,Li GR,et al.Molecular electronegativitydistance vector(MEDV-4):a two-dimensional QSAR method for the estimation and prediction of biological activities of estradiol derivatives.J Mol St-Th,2004,679:107-113.
7 Zhou Y,Sun LL,Mei H,et al.Estimation and prediction of relative retention indices of polychlorinated naphthalenes in GC with molecular electronegativity distance vector.Chromatographia,2006,64:565-570.
8 Liao LM,Mei H,Li JF,et al.Estimation and prediction on retention times of components from essential oil of Paulownia tomentosa flowers by molecular electronegativity-distance vector(MEDV).J Mol St-Th,2008,850:1-8.
9 Sutter JM,Peterson TA,Juts PC.Prediction of gas chromatographic retention indices of alkylbenzenes.Anal Chim Acta,1997,342:113-122.
10 Liao LM(廖立敏),Mei H(梅虎),Li JF(李建凤),et al.Prediction on retention times of components from essential oil of Tilia mongolica leaves by H-MEDV.Nat Prod Res Dev(天然产物研究与开发),2008,20:47-51.
Quantitative Structure-Retention Relationship(QSRR)of Volatile Constituents of Meconopsis integrifolia Franch
LAN Zuo-ping1,2,LIAO Li-min3,LIU Yu1,YU Yu1*1College of Pharmacy Chongqing Medical University,Chongqing 400016;2Chongqing Pharmaceutical College,Chongqing 400030,China;3College of Resource and Environment Science,Neijiang Normal University,Neijiang 641112,China
The concept of vectors of vertexes and their interaction were proposed to characterize the molecular structure of complicated samples.Through stepwise multiple regression(SMR),a model with 7 variables could be obtained by multiple linear regression(MLR).The correlation coefficient(R)of the model was 0.990 and the standard deviation(SD) was 1.325.Then the model was evaluated by the cross validation with the leave-one-out(LOO)procedure and the correlation coefficient(RCV)of 0.983 and standard deviations(SDCV)of 1.696 were obtained.The results showed that the vectors were superior in molecular structural characterization.The stability and predictability of the model was satisfactory.
Meconopsis integrifolia Franch;volatile organic compounds(VOC);structural descriptor;quantitative structure-retention relationship(QSRR)
1001-6880(2011)06-1091-05
2010-06-07 接受日期:2010-12-06
重庆市卫生局医学科研资助项目(2009-2-134);四川省教育厅青年基金项目(09ZB036)
*通讯作者 Tel:86-23-68485983;E-mail:yuyu3519@163.com.
O657.7
A
