一类拟三次系统的中心条件与极限环分支

潘雪军,郭远丽

(1.同济大学浙江学院，浙江 嘉兴 314051；2.浙江海宁高级中学，浙江 海宁 314400)

一类拟三次系统的中心条件与极限环分支

潘雪军1,郭远丽2

(1.同济大学浙江学院，浙江 嘉兴 314051；2.浙江海宁高级中学，浙江 海宁 314400)

研究了一类拟三次系统的奇点量、中心焦点判定与极限环分支问题,首先通过适当的变换将系统的原点(无穷远点)转化为原点,得到了系统原点的前21个奇点量,从而导出原点为中心和最高阶细焦点(细奇点)的条件,并分别给出了原点和无穷远点分支出4个极限环的实例.

拟三次系统;奇点量;中心条件;极限环分支

0 引 言

焦点量的计算对导出多项式微分系统中心条件、稳定性及研究由细焦点扰动产生极限环的问题具有重要意义.对原点为初等奇点系统的焦点量计算与极限环分支问题已有丰富的结果,一些数学工作者开始了无穷远点(赤道环)焦点量的计算及极限环分支问题的研究.

计算焦点量所用的方法是经典的形式级数法与后继函数法,但这些方法就目前的计算条件很难适用于复杂系统.文[1]和文[2]的作者分别指出初等奇点、高次奇点、无穷远点的奇点量的概念及计算方法,把焦点量和鞍点量的计算统一为奇点量的计算.并且对一些系统可以导出递推公式来计算奇点量,从而给出了一类计算多项式微分系统焦点量、鞍点量的新方法.但对于系统

(1)

相对应的拟解析系统

(2)

的中心条件与极限环分支研究结果非常罕见,文献[3]对拟二次系统进行过研究并给出了4个极限环的实例.文献[4]研究了一类拟三次的中心条件.笔者通过适当的变换把非解析的系统化为解析的系统研究,并相应地把原点或无穷远点转化为原点研究,同时考虑系统的中心条件,并分别给出了原点和无穷远点分支出4个极限环的实例.

1 预备知识

研究下面一类拟3次解析系统

(3)

X2=-B02x2+2A02xy+B02y2,Y2=A02x2+2B02xy-A02y2,
X3=(-B21-B30)x3+(-A21-3A30)x2y+(-B21+3B30)xy2+(-A21+A30)y3,
Y3=(A21+A30)x3+(-B21-3B30)x2y+(A21-3A30)xy2+(-B21+B30)y3.

其中λ,δ,Akj,Bkj均为实数,且λ≠0系统(3)δ=0经过复系数线性变换

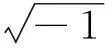
转换成

(4)

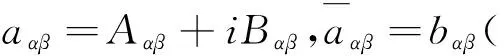
z=u(uv)(λ-3)/6,w=v(uv)(λ-3)/6.

转换成

(5)

由文献[1]中的方法得到:∀λ,系统5有6个基本Lie不变量

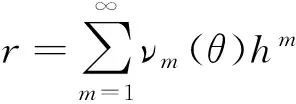
系统(3)δ=0的原点(λ>0)或无穷远点(λ<0)的中心条件与极限环分支可以转化为系统(5)原点的中心条件与极限环分支.系统(2)通过极坐标变换

转换成

(6)

其中

φk+1(θ)=cosθXk(cosθ,sinθ)+sinθYk(cosθ,sinθ),
ψk+1(θ)=cosθYk(cosθ,sinθ)-sinθXk(cosθ,sinθ).

2 系统的奇点量与中心条件

对于二维复微分自治系统:

(7)

且c00=1,cαα=0,α=1,2,…对于α≠β,有

(8)

其中∀α,β,当α<0或β<0时,aα,β=bα,β=cα,β=0.对任意的正整数m,μm是系统(7)的奇点量,且ν2m+1(2π)～iπμm,此处～是代数等价符号,其具体定义见[1].

由引理1,系统(3)δ=0原点或无穷远点的焦点量可由系统(5)原点的奇点量导出,显然,系统(3)δ=0的原点或无穷远点是中心当且仅当系统(5)原点所有奇点量μm=0.

根据引理1,使用Matwmatics软件包对于系统(5),奇点量公式的机器推导,得

定理1如果系统(5)的右端系数互为独立的复数,则系统(5)原点前21个奇点量公式为

(9)

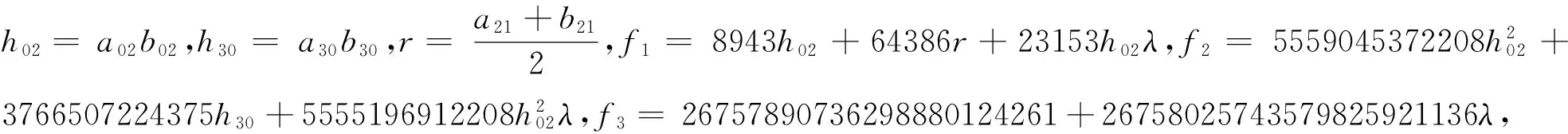
定理2如果系统(5)的右端系数互为独立的复数,则系统(5)原点前21个奇点量均为零,当且仅当下列条件之一成立:

条件I1:λ=0;

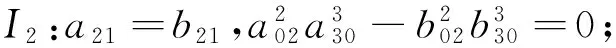
条件I3:a21=b21=0,λ=-5;

条件I4:a21=b21=a02=a30=0,λ=-1;

条件I5:a21=b21=b02=b30=0,λ=-1;

条件I6:a21=b21=a02=a30=0,λ=3;

条件I7:a21=b21=b02=b30=0,λ=3.

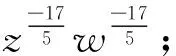
3 极限环分支

定理4当λ≠0,如果系统(5)的右端系数互为独立的复数,则系统(5)有18阶细临界奇点的充要条件是

定理5当λ≠0,如果系统(5)的右端系数互为独立的复数,则系统(5)有21阶细临界奇点的充要条件是

定理6当λ≠0系统(3)δ=0不可能是21阶细临界奇点.

g(h)=c0+c2h2+c8h8+c10h12+c12h12.

其中,c12=-(221513702/180075)有m个简单的零点,则当0<|ε|≪1,时,系统(5)在原点充分小的领域内且有m个小振幅的极限环,其位置分别在圆x2+y2=(kε)2(k=1,2,3…m)附近.相应地,系统(3)原点充分小的领域内且有m个极限环其位置分别在圆x2+y2=(kε)2(k=1,2,3…,m)附近.

证由文[4],ν1(2π)-1=e2πδλ,ν2m+1(2π)～3iπμ3m,由(9)得

(10)

由式(10)可证:

r(2π,εh)-εh=3πε13h[g(h)+ε2h2G(h,ε)]

(11)

其中,G(h,ε)在(0,0)点解析,由式(11)与隐函数存在定理即可得证.

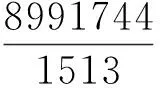
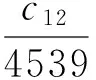
从而当0<|ε|≪1,时,系统(3)在原点充分小的领域内且有4个小振幅的极限环,其位置分别在圆x2+y2=(kε)2(k=1,2,3,4)附近.

g(h)=c0+c2h2+c8h8+c10h12+c12h12

其中,c12=-(1960169/1678635)有m个简单的零点,则当0<|ε|≪1时,系统(5)在原点充分小的领域内且有m个小振幅的极限环,其位置分别在圆x2+y2=(kε)2(k=1,2,3…,m)附近.相应地,系统(3)在赤道环的充分小的领域内且有m个极限环其位置分别在圆(x2+y2)-1=(kε)2(k=1,2,3…,m)附近.

证由文[4],ν1(2π)-1=e2πδλ,ν2m+1(2π)～3iπμ3m,由(9)得

(12)

由式(12)可证:

r(2π,εh)-εh=3πε13h[g(h)+ε2h2G(h,ε)]

(13)

其中,G(h,ε)在(0,0)点解析,由式(13)与隐函数存在定理即可得证.

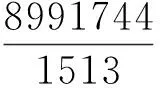
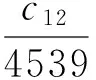
从而当0<|ε|≪1,时,系统(3)在赤道环的充分小的领域内且有4个小振幅的极限环,其位置分别在圆(x2+y2)-1=(kε)2(k=1,2,3,4)附近.

[1] 刘一戎,李继彬.论复自治微分系统的奇点量[J].中国科学：A辑,1989,32(3):245-255.

[2] 刘一戎.一类高次奇点与无穷远点的中心焦点理论[J].中国科学：A辑,2001,31(1):37-48.

[3] 刘一戎.拟二次系统的广义焦点量与极限环分支[J].数学学报,2002:45(4):671-682.

[4] 赵百利.一类拟三次系统的中心条件与极限环分支[J].黑龙江科技学院学报,2007:17(3):622-627.

[5] Liu Yirong , Chen Haibo. Stability and bifurcation of limit cycle of the equator in a class of cubic polynomial system [J]. Commuters and Mathematics with applications,2002,44:997-1005.

CenterConditionsandBifurcationofLimitCyclesin
AClassofQuasi-CubicSystems

PAN Xue-jun1, GUO Yuan-li2

(1.Tongji University Zhejiang College, Jiaxing 314051, China; 2. Haining Senior High School Zhejiang Province, Haining 314400, China)

This paper investigated the singular quantity, center conditions and bifurcation of limit cycles in a class of quasi-cubic systems changed the origin of the system which is infinite point to be origin, obtained twenty-first singular points and deduced the conditions for origin to be a center and the fine focus of the highest order provided the examples of that four limit cycles branched from the origin and the infinite point respectively as well.

quasi-cubic systems; singular quantity; center condition; bifurcation of limit cycles

10.3969/j.issn.1674-232X.2011.02.006

2010-08-29

潘雪军(1983—),男,浙江温岭人,助教，主要从事微分方程定性理论研究.E-mail: pxj115@163

O175.12MSC2010O193

A

1674-232X(2011)02-0119-05