一个状态控制问题的数学建模与求解
2011-11-22胡英武
胡英武
(金华职业技术学院,浙江金华 321017)
一个状态控制问题的数学建模与求解
胡英武
(金华职业技术学院,浙江金华 321017)
对互联网上的一个数学游戏的控制问题,进行了一般性推广,运用数学建模的方法给出了其基于有限域上的线性方程组的数学模型及求解.
有限域;状态向量;初始控制矩阵;复合变换;复合控制矩阵;最终效果矩阵
考虑互联网上的一个关灯游戏[1]:给定一个5×5方格的棋盘,每个方格有白色和黑色两种状态,当用鼠标点击其中任何一个方格时,则使这个方格自身及与之相邻的上下左右四个方格都改变状态(即原来是白色的则变成黑色,原来是黑色的则变成白色).对于处于棋盘边缘的16个方格,它们的这四个邻居可能不全存在,那么只考虑存在的方格.
假定棋盘的初始状态为所有方格全部为白色,问是否可以通过点击方格将棋盘的所有方格全部变为黑色.若可以,如何进行游戏,使点击鼠标的次数尽可能少(称为最优策略).
文[1]用抽象代数的变换理论建立了该游戏的数学模型.
1 问题的提出
本文利用有限域上的线性空间理论讨论m×n方格的棋盘问题,研究了棋盘从任一初始状态S0能否通过点击方格变为终止状态S1的操作可行性判定方法,以及操作可行时的具体操作(最优策略),较全面地解决了该问题.
2 模型的建立
定义1 若aij∈{0,1},则称矩阵Am×n=(aij)为m×n的二进制矩阵[2].特别地,1×n阶的二进制矩阵称为n维二进制向量.
若用0代表白色,1代表黑色,令l=mn,并将m×n棋盘的所有方格按从左到右,从上到下依次编号为1,2,…,l,则棋盘的任一状态对应与一个l维二进制向量S=(s1,s2,…,si,…sl),si∈{0,1}, i=1,2,…,l,称此向量S为棋盘的状态向量.
定义2 称l维二进制向量Li=(ai1,ai2,…,ail)(i=1,2,…l),为点击方格i对棋盘的控制作用(简称初始控制向量),其中aij=1,表示点击方格i能控制方格j;aij=0,表示点击方格i不能控制方格j(j=1,2,…,l).
称由初始控制向量Li为行向量构成的二进制矩阵A为初始控制矩阵.

定义3 设F2={0,1},F2上定义四则运算,其运算法则如下:

显然,F2={0,1}对于上述运算构成一个域(称此域为二元有限域).
定义4 设V1=(b1,b2,…,bl),V2=(c1,c2,…,cl)是两个l维二进制向量,定义
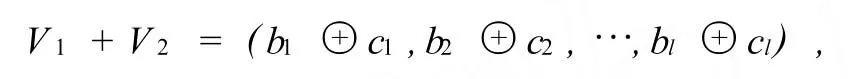
称此运算为l维二进制向量加法.k∈F2,定义
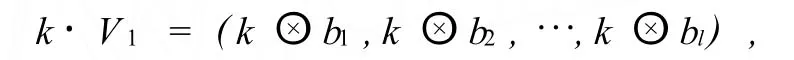
称此运算为l维二进制向量数乘.
显然,对于这样定义的l维二进制向量的加法与数乘,有
定理1[3]设V是所有l维二进制向量组成的集合,F2={0,1},则对于l维二进制向量加法与数乘,V是数域F2上的向量空间.称向量空间V为l维二进制向量空间.
定义5 设β,αi∈V(i=1,2,…,r),若存在xi∈F2(i=1,2,…,r),使β=x1·α1+x2·α2+…+xr·αr,则称β是α1,α2,…,αr二进制线性组合(简称线性组合).
到此,我们给出问题的数学模型如下:
已知m×n方格棋盘的初始状态向量S0,终止状态向量S1和初始控制矩阵A,问
1)通过操作点击方格能否将初始状态向量S0变成终止状态向量S1,即给出可行性判别方法;
2)操作可行时如何具体操作,即给出算法.
3 模型的求解
定义6 将二进制矩阵的第i行加到(按l维二进制向量加法)第j行去,称这种变换为二进制矩阵的复合变换[4].将初始控制矩阵A的第i行加到第j行的复合变换记为Lj+Li,初始控制矩阵A经过一系列复合变换得到的矩阵称为复合控制矩阵.
若复合控制矩阵的某个行向量是复合变换(Lj+Lk+Li)+Li的结果,由运算“+,⊕”有(Lj+Lk+Li) +Li=Lj+Lk,即点击方格i两次或偶数次,此操作的作用将取消,为使点击方格次数尽可能少,这种重复操作应避免.于是排除上述情况后的复合控制矩阵的行向量表示若干个方格(各点击一次)对棋盘的复合控制效果.
定理2 设α1,α2,…,αr是r个线性无关的l维二进制向量,则由α1,α2,…,αr生成的子空间V(α1,α2,…,αr)总共含有2r个不同的向量.
证因为α1,α2,…,αr的所有线性组合都可以表示为

每个线性组合与其坐标(x1,x2,…,xr)一一对应,所以,由α1,α2,…,αr生成的子空间V(α1,α2,…,αr)总共含有2r个不同的向量.
推论如果初始控制矩阵A的秩为r,则
1)通过操作点击方格总共可以使棋盘达到2r种不同的状态,反之亦然;
证因为R(A)=r,所以存在矩阵A的r个行向量构成它的行向量组的极大无关组.设Lk1,Lk2,…,Lkr是矩阵A的行向量组的一个极大无关组,显然Lk1,Lk2,…,Lkr的线性组合
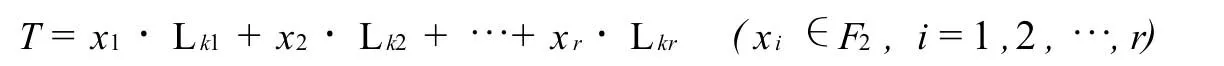
与点击方格的操作效果一一对应,即生成子空间V(Lk1,Lk2,…,Lkr)中的向量与点击方格的操作效果一一对应.所以1)得证.又因m×n的棋盘共有2l种状态,2)得证.
注 推论说明,棋盘所能达到的状态由初始控制矩阵A的秩唯一决定.
定理3 设m×n棋盘的初始状态向量S0,终止状态向量S1,初始控制矩阵A的秩为r,Lk1,Lk2,…,Lkr是矩阵A的行向量组的一个极大无关组,则游戏可从初始状态S0变到终止状态S1的充分必要条件为:存在xi∈F2(i=1,2,…,r),使
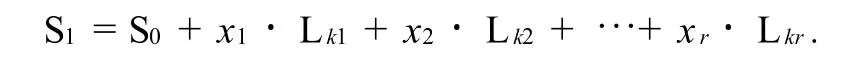
证1)对于棋盘的某一状态Si,在点击第k个方格后,转移到另一种状态Sj这一过程可以用状态向量和初始控制向量之和表示为Sj=Si+Lk,反之亦然.
2)从初始状态S0变到终止状态S1,等价于从初始状态S0出发点击某几个方格各一次可变到终止状态S1.又因为点击方格的初始控制向量L1,L2,…,Ll都是Lk1,Lk2,…,Lkr的线性组合,综合1),2)即得到定理3的证明.
显然,由于复合控制矩阵的行向量都是某几个初始控制向量相加得到,所以经过复合变换后新旧矩阵所能达到的总效果不变.
定义7 若二进制矩阵B是二进制矩阵C经一系列复合变换后得到的,则称矩阵B与C的控制效果等价(简称矩阵B,C等价),记为B∽C.
显然,关系“∽”为等价关系,复合变换是一种等价变换.
定理4[3]若B,C都是二进制矩阵,则
1)如果B∽C,则R(B)=R(C)(即复合变换不改变矩阵的秩);
2)如果B∽C,则B,C的行向量组的极大无关组等价(即可以相互表出).(证明略)
定义8 如果矩阵M的非零行的第1个不为0(为1)的元素所在列的其余元素均为0,零行全部位于矩阵M的下部,则称该矩阵为最简阶梯型矩阵.
定理5[3]若二进制矩阵N的秩为r,则必可经过一系列复合变换将矩阵N变成仅有r个非零行向量的最简阶梯型矩阵.称由初始控制阵A经过一系列复合变换得到的最简阶梯型矩阵Q为A的最终效果矩阵.(证明略)
定理6 设初始控制阵A的秩为r,Q是初始控制阵A的最终效果矩阵,S0,S1分别为游戏的初始状态向量和终止状态向量,Q1,Q2,…,Qr是最终效果矩阵Q的非零行向量,则游戏可从初始状态S0变到终止状态S1的充分必要条件为存在xi∈F2(i=1,2,…,r),使
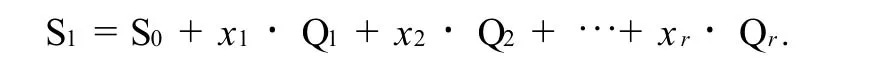
证由定理4和定理5知,Q1,Q2,…,Qr与矩阵A的行向量组的一个极大无关组等价.再由定理3就得到定理6的证明.
又根据“+,⊕”的性质,可将定理6中的S1=S0+x1·Q1+x2·Q2+…+xr·Qr改为

下面我们给出原问题的可行性判别与求解方法.
1)通过一系列复合变换将初始控制阵A变为最终效果阵Q,于是得到最终效果阵Q的r个非零行向量Q1,Q2,…,Qr;
2)令S0+S1=x1·Q1+x2·Q2+…+xr·Qr.若此组合式有解,则棋盘能从初始状态S0变成终止状态S1;否则,棋盘不能从初始状态S0变成终止状态S1;
3)如果棋盘能从初始状态S0变成终止状态S1,则根据2)的解中等于1的xi所对应的Qi即可得到将初始状态S0变成终止状态S1的点击操作方法.
4 模型检验
实例,考虑3×5的棋盘,其初始控制阵为

棋盘的初始状态为(0,0,0,0,0,0,0,0,0,0,0,0,0,0,0),问:
通过点击方格能否达到终止状态(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1)与(1,1,1,1,1,1,1,1,1,1,1, 1,0,1,1);
若能达到终止状态,如何点击方格.
解 对初始控制阵A施行一系列复合变换后得最终效果阵Q,

由于R(A)=R(Q)=12<15,所以,点击方格只能达到棋盘所有可能状态215种中的212种,即所有可能状态中的
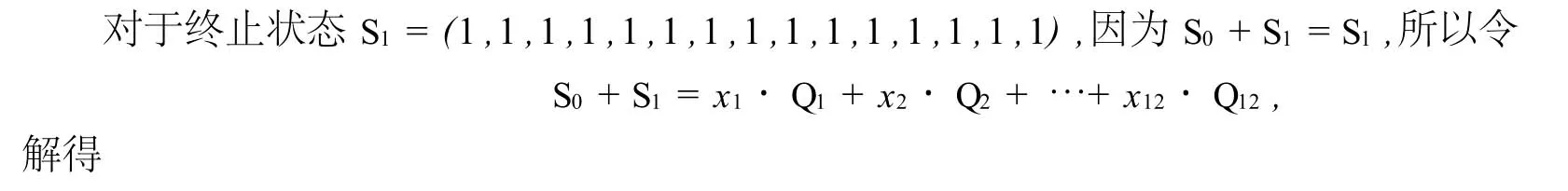
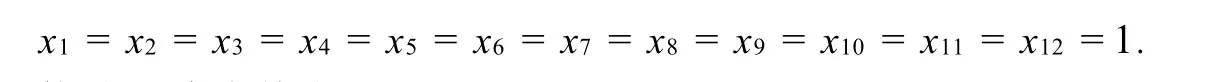
因而,从初始状态S0,能达到终止状态S1.
由矩阵Q的前12行,可知只需点击第2,9,10,11,14,15方格各一次就可将初始状态S0,变成终止状态S1.
注 若由A到Q的变换方法不唯一,则可能产生不同的方法,但最少点击方格次数相同.如点击第1,3,7,10,11,13方格各一次也可将初始状态S0,变成终止状态S1.
对于终止状态S1=(1,1,1,1,1,1,1,1,1,1,1,1,0,1,1),因为S0+S1=S1,所以令
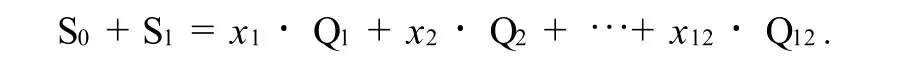
此式无解,因而,从初始状态S0不能达到终止状态S1.
5 模型评价
我们首先定义了二元域上的二进制向量空间,然后将此游戏转化成一个二元域上的线性方程组的解的存在性问题,这个线性方程组是定义在二元域F2上,不是我们所熟知的定义在R上的线性方程组.所幸的是,F2上的线性方程组解的存在性理论[3]以及求解方法[5]完全和R上的线性方程组一样,甚至求解过程还要简单,因为F2远比R简单.
[1] 周昊.“关灯”游戏中的代数学[J].数学的实践与认识,2007,37(11):132-140.
[2] 程德文,张建涛.一个游戏难题的数学建模与求解[J].数学的实践与认识,2005,35(8):1-4.
[3] 冯克勤.有限域[M].长沙:湖南教育出版社,1998.
[4] 李炯生,查建国.线性代数[M].合肥:中国科学技术大学出版社,1989.
[5] Hungerford T W.Algebra[M].New York:Springer-Verlag,1974.
The Mathematical Modeling and Solving for a State Control Problem
HU Ying-w u
(Jinhuacollege of Profession and Technology of China,Jinhua,Zhejiang 321017,China)
We conduct the general popularization to the state control of a mathematical game on internet and use the method of mathematical modeling to show the mathematical model of linear equation system based on finite field and its solving.
finite field;state variable;initial control matrix;composite convert;composite control matrix;final effect matrix
O141.4
A
1672-1454(2011)03-0168-05
2008-08-18;[修改日期]2008-12-01
浙江省教育厅科研项目(Y201017888);金华职业技术学院青年教改项目(10QN18)
