为“线性代数与空间解析几何”课程开发数学建模教学插件研究

黄廷祝, 张 勇

(电子科技大学数学科学学院,成都 610054)

为“线性代数与空间解析几何”课程开发数学建模教学插件研究

黄廷祝, 张 勇

(电子科技大学数学科学学院,成都 610054)

论述了数学基础课中开发数学建模教学插件的必要性和应用前景,并结合线性代数与空间解析几何课程中线性变换知识、数学建模、Matlab数学软件设计开发了教学插件,提出了开发过程的设计思想.

线性代数;线性变换;数学建模;教学插件;Matlab数学软件

1 引 言

在数学基础课程的教学改革中,比如,由于“微积分”、“线性代数”等课程内容多,课时紧,很多情况下,教师的教学都难以摆脱一种灌输的教学,这样的教学不利于培养学生的创新性思维.为了开创新的教学模式,提升教学效果,目前广泛开展的“数学实验”和“数学建模”课程取得良好的效果.而这些课程的开设往往和这些基础课分开开设.在形式上造成一定的脱节.如果能够在基础课的教学过程中,就直接利用“数学实验”和“数学建模”课程中的好的教学形式和教学设计思想,那么必将产生更直接更快捷的效果.

为了便于配合基础课程教学,我们陆续开发数学建模教学插件.在数学基础课教学乃至专业课教学中,开发数学建模教学插件的有这样一些好处：

(i)增加学生对相关知识的认知程度;

(ii)有利于学生熟悉课程知识的应用背景、应用过程;

(iii)让学生早期接受初期的实践课题,启发创造性思维.

另外,这些教学插件内容简练,相对独立,可以选择性的应用.比如,以一个甚至多个知识点结合一个实际应用问题的建模过程开发插件.

下面我们先讨论数学建模的应用过程和特性,再结合实例探讨开发过程.

2 发挥数学建模培养创新思维的优势

对于数学建模在数学基础课程中的重要性和应用实践有较多论述,其应用的必要性、重要性,实践的有效性得到了广大师生的认同,其应用价值有目共睹.

数学建模教学及其在其他课程中的教学实践之所以产生如此广泛的良好影响,与其本身蕴含的特性分不开.数学建模的基本过程由问题分析、问题简化、模型建立、模型求解、模型检验、模型应用组成.这个过程也就是科研和工程中解决问题的一般过程,可以让学生尽早进入科研与工程实践.将这些实践教学用于学生学习大学低年级数学基础课,可以大大提高学生对数学的学习兴趣,认识到数学的重要性,有利于创新性思维.

3 教学插件的开发

3.1 知识点与实际问题的选择.

在教学插件的开发之前,需要在线性代数教学中的一些难点中选择知识点,并结合恰当的实际问题开发插件.比如,可以选择线性相关性、特征值与特征向量、线性变换等内容开发插件.在整个开发过程中,选择恰当的实际问题显得较难.另外,如果选择的问题求解过程可以通过直观的方式进行展示,则得到的教学效果会更好.

3.2 开发过程.

下面以线性变换作为知识点,以2D图形与游戏开发为实际背景,探讨一个教学插件的开发过程.

(i)问题描述及问题背景.

假定现在要在平面上旋转一个物体,需要绘制物体的旋转过程.由于绘制过程需要知道物体上各点的坐标,而旋转过程中物体上点的坐标是不断变化的.因此,绘制过程需要跟踪物体坐标的变换.

问题可以归结为已知旋转角度θ,旋转前P点的坐标为(x,y),计算旋转后点坐标的为P′(x′,y′).这里P点代表任意待旋转的点.

(ii)分析与建模.

为了计算矩阵M,不妨先从特殊点或向量的旋转开始分析.设u=(1,0)T,v=(0,1)T.u和v可以看作x轴正向,y轴正向的单位向量,也可以看作为x,y轴上两个点的坐标.同时也是2D空间中的一组基向量.设u′,v′分别为u,v旋转后的向量.

将u和v代入(1),可得

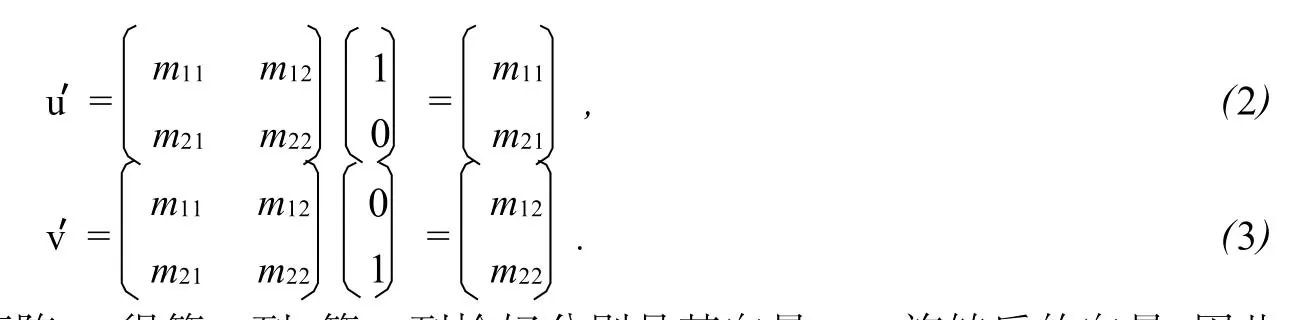
由(2),(3)式可知,所求旋转矩阵M得第1列,第2列恰好分别是基向量u,v旋转后的向量.因此找出u,v旋转后的u′,v′,分别填入旋转矩阵的第1列,第2列即得旋转矩阵M.

(iii)模型求解.

下面计算u′,v′.

记旋转角度逆时针方向为正,顺时针方向为负.则在已知u,v逆时针旋转θ后的向量u′,v′如下(见图1)

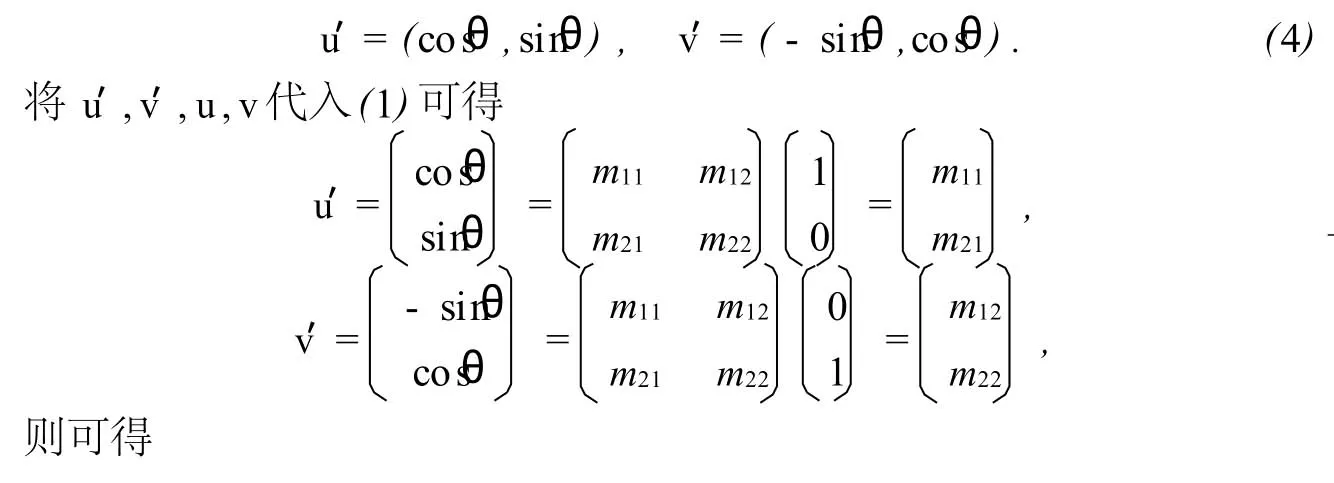
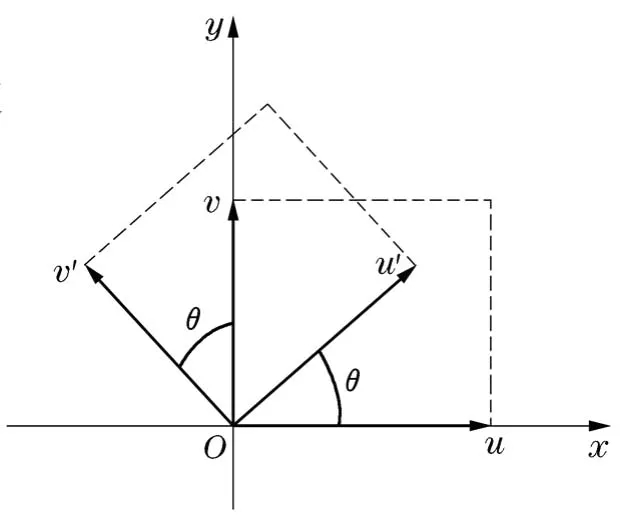
图1 基向量的旋转

(iv)应用演示.

在这个阶段将模型的求解过程以及应用过程用直观的动画形式进行演示.

以一个旋转一个单位正方形的过程来描述,并用Matlab设计动画演示,动画效果见图2,图3:

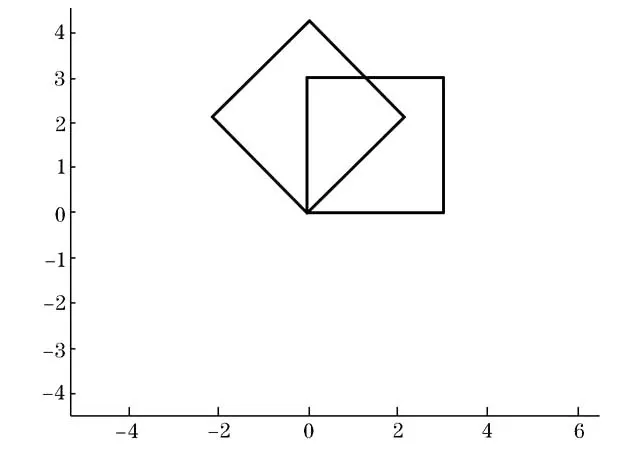
图2 旋转后的图形重叠

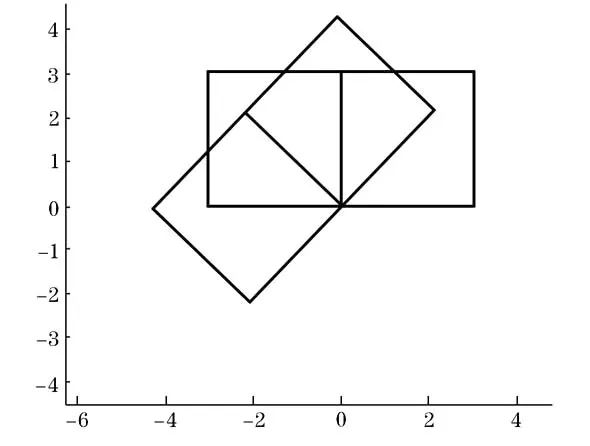
图3 旋转,后的图形重叠

(v)探索阶段.

前面的推导只就如何求出旋转变换矩阵而展开,还没有挖掘其深层次的含义和用途.因此,为了升华所学知识,可以给出以下几个问题供学生探索,开展创新性思维训练,培养创新实践能力:

①先旋转角度θ1,后旋转角度θ2的最后图形效果应该等同于一次旋转角度θ1+θ2,能否结合旋转变换矩阵M进行论证.

②请结合旋转变换矩阵的几何意义,用一句话概括构造旋转变换矩阵的方法.

③如果在绘图过程中需要撤销刚实施的旋转变换,应该如何变换点的坐标,恢复旋转前的图形?

当然,还可以启发学生去探索,如何将这里的结论推广到3D空间中绕坐标轴的旋转.

4 应用前景

显然,我们开发的教学插件内容丰富又精炼,融合了数学模型、数学建模过程及其应用的线性代数基本知识,内容具有综合性强、涉及面广,可以在较短时间内让学生体会到数学知识应用的乐趣,体会到解决实际问题的思路和过程.既能让学生尽早接触实际问题,又能让学生较快地接受解决问题的思维训练,有利于培养学生的创造性思维.有利于促使学生开展研究型学习,也有利于开展研究型教学.目前不少综合性大学都在由教学型大学向研究型大学转变,教师教学思维的转变和培养是关键,同样,培养研究型学习的学生同样重要.因此,利用数学建模教学插件在基础课程,乃至专业课程中进行应用,有利于这些目标的实现.

我们相信,发挥数学建模课程本身的实践性和诸多优点,将其用于其他课程的实践将为我们实现创新性人才培养发挥重要作用.

[1] 黄廷祝,成孝予.线性代数与空间解析几何[M].3版.北京：高等教育出版社,2008.

[2] (美)吉奥丹诺(Frand R.Giordano),等.数学建模[M].叶其孝,姜启源等,译,3版.北京：机械工业出版社,2005.

[3] Fletcher Dunn,Ian Parberry.3D数学基础：图形与游戏开发[M].史银雪,陈洪,王荣静,译.北京：清华大学出版社,2005.

[4] 冷劲松,黄廷祝,成孝予.《数学实验》课程的实验题材研究[J].工科数学,2001,17(2)：86-88.

[5] 汪新凡.“分层教学·分类指导”教学模式研究[J].教学研究,2005,28(1)：42-44.

[6] 陈世发,薛德黔.Matlab在高等数学教学中的应用[J].福建电脑,2006(10)：214.

[7] 尚月强,杨一都.Matlab及其在数学建模中的应用[J].贵州师范大学学报(自然科学版),2005,23(1)：77-81.

O151.2;TP311.52

C

1672-1454(2011)03-0161-03

2008-10-06

教育部普通高等教育教改项目